AP 9th Class Maths Important Questions Chapter 11 Areas

These AP 9th Class Maths Important Questions 11th Lesson Areas will help students prepare well for the exams.

AP State Syllabus 9th Class Maths 11th Lesson Important Questions and Answers Areas

Question 1.
Fill in the following table with suitable units:

Solution:

Question 2.
Find the distance between the parallel lines of a parallelogram whose base is given 12.5 cm. and area is 75 cm².
Solution:
Base of parallelogram = b = 12.5 cm
Area of parallelogram = bh = 75 sq.cm.
Height of parallelogram = \(\frac{75}{12.5}\) = 6 cm

Question 3.
The following statements belong to which quadrilateral area and express them in symbolic form.
i) Half of the product of base and height.
ii) Half of the product of it’s diagonals.
Solution:
i) Area of triangle = 1/2 × base × height
ii) Area of Rhombus = 1/2 × diagonal × diagonal₂

Question 4.
In the given figure \(\overline{\mathbf{B A}}\) ⊥ \(\overline{\mathbf{E A}}\), \(\overline{\mathbf{B E}}\) ⊥ \(\overline{\mathbf{E D}}\) and \(\overline{\mathbf{B D}}\) ⊥ \(\overline{\mathbf{C D}}\).

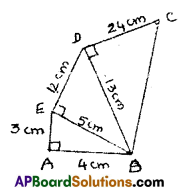
Find the area of the pentagon ABCDE.
Solution:
Given \(\overline{\mathbf{B A}}\) ⊥ \(\overline{\mathbf{E A}}\), \(\overline{\mathbf{B E}}\) ⊥ \(\overline{\mathbf{E D }}\), \(\overline{\mathbf{B D}}\) ⊥ \(\overline{\mathbf{C D }}\)
Area of Pentagon = area of ΔABE + area of ΔBED + area of ΔBDC
= \(\frac{1}{2}\) × AB × AE + \(\frac{1}{2}\) × BE × DE + \(\frac{1}{2}\) × BD × CD
= \(\frac{1}{2}\) × 4 × 3 + \(\frac{1}{2}\) × 5 × 12 + \(\frac{1}{2}\) × 13 × 24
= 6 cm² + 30 cm² 156 cm²
= 192 cm²

Question 5.
□ABCD is a parallelogram where \(\overline{\mathbf{A B}}\) || \(\overline{\mathbf{C D}}\). E is a point on \(\overline{\mathbf{C D}}\) If the area of ΔABE = 14.2 cm², find the area of the parallelogram ABCD. Support your answer with a proper reason.
Solution:
Area of ΔABE from figure = 14.2 cm

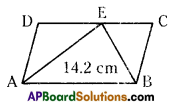
From theorem.
Area of ΔADE + area of ΔBCE – area of ΔAEB
∴ Area of ΔADE = area of ΔBCE,
x + x = area of ΔAEB
2x = 14.2 cm
x = \(\frac{14.2}{2}\) = 7.1 cm
∴Area of ΔADE = area of ΔBEC

Question 6.
Give any two examples for each from your daily life to find
i) Area of triangle
ii) Area of rectangle.
Solution:
i) Uses of Area of triangle :
a) To payment the white wash of a triangular wall
b) To prepare canvas of a boat,

ii) Uses of area of rectangle :
a) To payment the white wash of a rect-angular wall.
b) To measure length of a rectangular plot.

Question 7.
ABCD is a parallelogram. ABEM is a rectangle on the same base AB as shown in the figure. If AB = 10 cm, DM = 3cm and BE = 7 cm, find the area of the quadrilateral ABED.

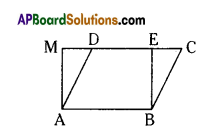
Solution:
Area of rectangle ABEM = AB × BE
=10 × 7 = 70 sq.cm.
Area of ΔAMD = \(\frac{1}{2}\) × AM × MD
= \(\frac{1}{2}\) × 7 × 3 = 10.5 sq.crn
Area of quadrilateral ABED
= Area of ABEM – Area of ΔAMD
= 70 – 10.5 = 59.5 sq.cm.

Question 8.
PQRS is a rhombus. Find the ratio of area of rhombus PQRS to the area of triangle PQR.
Solution:

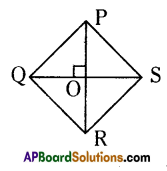
Area of Rhombus = \(\frac{1}{2}\) × PR × QS
Area of ΔPQR = \(\frac{1}{2}\) × PR × QO
Ratio = \(\frac{1}{2}\) × PR × QS : \(\frac{1}{2}\) × PR × QO
= QS : QO
= 2 (QO) : QO = 2 : 1

Question 9.
In ΔABC, AB = 12 cm and BC = 6.5 cm, ∠ABC = 90°. If D is the mid-point of \(\overline{\mathbf{A C}}\), find the area of ΔABD and ΔBCD. What did you observe?
Solution:
In ΔABC, ∠B = 90°, AB = 12 cm and BC = 6.5 cm

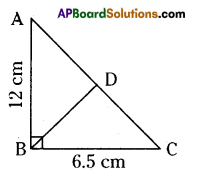
Area of ΔABC = \(\frac{1}{2}\) × BC × AB
= \(\frac{1}{2}\) × 6.5 × 12
= 39 sq. cm.
From theorem, D is a mid point of AC.
So, areas of ΔABD and ABDC are same.
∴ ΔABD + ΔBDC = ΔABC