Use these Inter 2nd Year Maths 2B Formulas PDF Chapter 1 Circle to solve questions creatively.
Intermediate 2nd Year Maths 2B Circle Formulas
→ The locus of a point in a plane such that its distance from a fixed point in the plane is always the same is called a circle.
→ The equation of a circle with centre (h, k) and radius r is (x – h)2 + (y – k)2 = r2
→ The equation of a circle in standard form is x2 + y2 = r2.
→ The equation of a circle in general form is x2 + y2 + 2gx + 2fy + c = 0 and its centre is (-g, -f), radius is \(\sqrt{g^{2}+f^{2}-c}\).
![]()
→ The intercept made by x2 + y2 + 2gx + 2fy + c = 0
- on X-axis is 2\(\sqrt{g^{2}-c}\) if g2 > c.
- on Y-axis is 2\(\sqrt{f^{2}-c}\) if f2 > c.
→ If the extremities of a diameter of a circle are (x1, y1) and (x2, y2) then its equation is (x – x1) (x – x2) + (y – y1) (y – y2) = 0
→ The equation of a circle passing through three non-collinear points (x1, y1), (x2, y2) and (x3, y3) is
\(\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\) = (x2 + y2) + \(\left|\begin{array}{lll}
c_{1} & y_{1} & 1 \\
c_{2} & y_{2} & 1 \\
c_{3} & y_{3} & 1
\end{array}\right|\) x + \(\left|\begin{array}{lll}
x_{1} & C_{1} & 1 \\
x_{2} & C_{2} & 1 \\
x_{3} & C_{3} & 1
\end{array}\right|\) y + \(\left|\begin{array}{lll}
x_{1} & y_{1} & C_{1} \\
x_{2} & y_{2} & C_{2} \\
x_{3} & y_{3} & C_{3}
\end{array}\right|\) = 0.
where ci = – (xi2 + yi2)
→ The centre of the circle passing through three non-collinear points (x1, y1), (x2, y2) and (x3, y3) is
\(\left[\frac{\left|\begin{array}{lll}
c_{1} & y_{1} & 1 \\
c_{2} & y_{2} & 1 \\
c_{3} & y_{3} & 1
\end{array}\right|}{(-2)\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|}, \frac{\left|\begin{array}{lll}
x_{1} & c_{1} & 1 \\
x_{2} & c_{2} & 1 \\
x_{3} & c_{3} & 1
\end{array}\right|}{(-2)\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|}\right]\)
![]()
→ The parametric equations of a circle with centre (h, k) and radius (r ≥ 0) are given by
x = h + r cos θ
y = k + r sin θ 0 ≤ 6 < 2π.
→ A point P(x1, y1) is an interior point or on the circumference or an exterior point of a circles S = 0 ⇔ S11 \(\frac{<}{>}\) 0.
→ The power of P(x1, y1) with respect to the circle S = 0 is S11.
→ A point P(x1, y1) is an interior point or on the circumference or exterior point of the circle S = 0 ⇔ the power of P with respect to S = 0 is negative, zero and positive.
→ If a straight line through a point P(x1, y1) meets the circle S = 0 at A and B then the power of P is equal to PA. PB.
→ The length of the tangent from P(x1, y1) to S = 0 is \(\sqrt{S_{11}}\).
→ The straight line l = 0 intersects, touches or does not meet the circles = 0 according as l < r, l = r or l > r where l is the perpendicular distance from the centre of the circle to the line l = 0 and r is the radius.
→ For every real value of m the straight line y = mx ± r \(\sqrt{1+m^{2}}\) is a tangent to the circle x2 + y2 = r2.
→ If r is the radius of the circle S = x2 + y2 + 2gx + 2fy + c = 0 then for every real value of m the straight line y + f = m(n + g) ±r + m2 will be a tangent to the circle.
→ If P(x1, y1) and Q(x2, y2) are two points on the circle S = 0 then the secant’s \((\stackrel{\leftrightarrow}{P Q})\) equation is S1 + S2 = S12
→ The equation of tangent at (x1, y1) of the circle S = 0 is S1 = 0.
→ If θ1, θ2 are two points on S = x2 + y2 + 2gx + 2fy + c = 0 then the equation of the chord joining the points θ1, θ2 is
(x + g) cos \(\left(\frac{\theta_{1}+\theta_{2}}{2}\right)\) + (y + f) sin \(\left(\frac{\theta_{1}+\theta_{2}}{2}\right)\) = r cos \(\left(\frac{\theta_{1}-\theta_{2}}{2}\right)\)
→ The equation of the tangent at θ of the circle S = 0 is (x + g) cos θ + (y + f) sin θ = r.
→ The equation of normal at (x1, y1) of the circle
S = 0 is (x – x1) (y1 + f) – (y – y1) (x1 + g) = 0.
![]()
→ The chord of contact of P(x1 y1) (exterior point) with respect to S = 0 is S1 = 0.
→ The equation of the polar of a point P(x1, y1) with respect to S = 0 is S1 = 0.
| P(x1, y1) | Tangent at P | Chord of contact at p | Polar of P |
| (i) Interior of the circle | Does not exist | Does not exist (not defined) |
S1 = 0 (P is different from the centre of the circle) |
| (ii) On the circle | S1 = 0 | S1 = 0 | S1 = 0 |
| (iii) Exterior of the circle | Does not exist | S1 = 0 | S1 = 0 |
→ The pole of lx + my + n = 0 with respect to S = 0 is
\(\left(-g+\frac{l r^{2}}{l g+m f-n},-f+\frac{m r^{2}}{l g+m f-n}\right)\)
→ Where r is the radius of the circle. The polar of P(x1, y1) with respect to S = 0 passes through Q(x2, y2) ⇔ the polar of Q with respect to S – 0 passes through P.
→ The points (x1, y1) and (x2, y2) are conjugate points with respect to S = 0 if S12 = 0
→ Two lines l1x = m1y + n1 = 0, l2x + m2y + n2 = 0 are conjugate with respect to x2 + y2 = a2 ⇔ (l1l2 + m1m2) = n1n2
→ Two points P, Q are said to be inverse points with respect to S = 0 if CP. CQ = r2 where C is the centre and r is the radius of the circle S = 0.
→ If (x1, y1) is the mid-point of a chord of the circle S = 0 then its chord equation is S1 = S11.
→ The pair of common tangents to the circles S = 0, S’ = 0 touching at a point on the lines segment \(\overline{\mathrm{C}_{1} \mathrm{C}_{2}}\) (C1, C2 are centres of the circles) is called transverse pair of common tangents.
→ The pair of common tangents to the circles S = 0, S’ = 0 intersecting at a point not in \(\overline{\mathrm{C}_{1} \mathrm{C}_{2}}\) is called as direct pair of common tangents.
![]()
→ The point of intersection of transvese (direct) common tangents is called internal (external) Centre of similitude.
| Situation | No of common tangents |
| 1. \( \overline{C_{1} C_{2}} \) > r1 + r2 | 4 |
| 2. r1 + r2 = \( \overline{C_{1} C_{2}} \) | 3 |
| 3. |r1 – r2| < \( \overline{C_{1} C_{2}} \) < r1 + r2 | 2 |
| 4. C1C2 = |r1 – r2| | 1 |
| 5. C1C2 < |r1 – r2| | 0 |
→ The combined equation of the pair of tangents drawn from an external point P(x1, y1) to the circle S = 0 is SS11 = S21.
Equation of a Circle:
The equation of the circle with centre C (h, k) and radius r is (x – h)2 + (y – k)2 = r2.
Proof:
Let P(x1, y1) be a point on the circle.
P lies in the circle ⇔ PC = r ⇔ \(\sqrt{\left(\mathrm{x}_{1}-\mathrm{h}\right)^{2}+\left(\mathrm{y}_{1}-\mathrm{k}\right)^{2}}\) = r
⇔ (x1 – h)2 + (y1 – k)2 = r2.
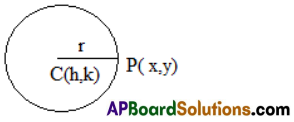
The locus of P is (x – h)2 + (y – k)2 = r2.
∴ The equation of the circle is (x – h)2 + (y – k)2 = r2.
Note: The equation of a circle with centre origin and radius r is (x – 0)2 + (y – 0)2 = r2
i.e., x2 + y2 = r2 which is the standard equation of the circle.
Note: On expanding equation (1), the equation of a circle is of the form x2 + y2 + 2gx + 2fy + c = 0.
Theorem: If g2 + f2 – c ≥ 0, then the equation x2 + y2 + 2gx + 2fy + c = 0 represents a circle with centre (- g, – f) and radius \(\sqrt{g^{2}+f^{2}-c}\).
Note: If ax2 + ay2 + 2gx + 2fy + c = 0 represents a circle, then its centre = \(\left(-\frac{g}{a},-\frac{f}{a}\right)\) and its radius \(\frac{\sqrt{\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{ac}}}{|\mathrm{a}|}\).
Theorem: The equation of a circle having the line segment joining A(x1, y1) and B(x2, y2) as diameter is (x – x1) (x – x2) + (y – y1) (y – y2) = 0.
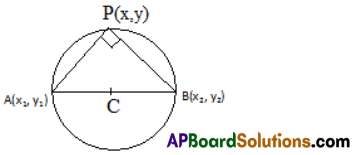
Let P(x, y) be any point on the circle. Given points A(x1, y1) and B(x2, y2).
Now ∠APB = \(\frac{\pi}{2}\). (Angle in a semi circle.)
Slope of AP. Slope of BP = – 1
⇒ \(\frac{y-y_{1}}{x-x_{1}} \frac{y-y_{2}}{x-x_{2}}\) = – 1
⇒ (y – y2) (y – y1) = – (x – x2) (x – x1) = 0
⇒ (x – x2) (x – x1) + (y – y2) (y – y1) = 0
Definition: Two circles are said to be concentric if they have same center.

The equation of the circle concentric with the circle x2 + y2 + 2gx + 2fy + c = 0 is of the form x2 + y2 + 2gx + 2fy + k = 0.
The equation of the concentric circles differs by constant only.
Parametric Equations of A Circle:
Theorem: If P(x, y) is a point on the circle with centre C(α, β) and radius r, then x = α + r cosθ, y = β + r sin θ where 0 ≤ θ < 2π.
Note: The equations x = α + r cos θ, y = + r sin θ, 0 ≤ θ < 2π are called parametric equations of the circle with centre (α, β) and radius r.
Note: A point on the circle x2 + y2 = r2 is taken in the form (r cos θ, r sin θ). The point (r cos θ, r sin θ) is simply denoted as point θ.
Theorem:
(1) If g2 – c > 0 then the intercept made on the x axis by the circle x2 + y2 + 2gx + 2fy + c = 0 is 2\(\sqrt{g^{2}-a c}\)
(2) If f2 – c >0 then the intercept made on the y axis by the circle x2 + y2 + 2gx + 2fy + c = 0 is 2\(\sqrt{f^{2}-b c}\)
Note: The condition for the x-axis to touch the circle
x2 + y2 + 2gx + 2fy + c = 0 (c > 0) is g2 = c.
Note: The condition of the y-axis to touch the circle
x2 + y2 + 2gx + 2fy + c = 0 (c > 0) is f2 = c.
Position of Point:
Let S = 0 be a circle and P(x1, y1) be a point I in the plane of the circle. Then
- P lies inside the circle S = 0 ⇔ S11 < 0
- P lies in the circle S = 0 ⇔ S11 = 0
- Plies outside the circle S = 0 ⇔ S11 = 0
Power of a Point:
Let S = 0 be a circle with centre C and radius r. Let P be a point. Then CP2 – r2 is called power of P with respect to the circle S = 0.
Theorem: The power of a point P(x1, y1) with respect to the circle S = 0 is S11.
Theorem: The length of the tangent drawn from an external point P(x1, y1) to the circle s = 0 is \(\sqrt{\mathrm{S}_{11}}\).
![]()
Theorem: The equation of the tangent to the circle S = 0 at P(x1, y1) is S1 = 0.
Theorem: The equation of the normal to the circle S = x2 + y2 + 2gx + 2fy + c = 0 at P(x1, y1) is
(y1 + f) (x – x1) – (x1 + g) (y – y1) = 0.
Corollary: The equation of the normal to the circle x2 + y2 = a2 at P(x1, y1) is y1x – x1y = 0.
Theorem: The condition that the straight line lx + my + n = 0 may touch the circle x2 + y2 = a2 is n2 = a2(l2 + m2) and the point of contact is \(\left(\frac{-a^{2} 1}{n}, \frac{-a^{2} m}{n}\right)\).
Proof:
The given line is lx + my + n = 0 …… (1)
The given circle is x2 + y2 = r2 ……. (2)
Centre C = (0, 0), radius = r
Line (1) is a tangent to the circle (2)
⇔ The perpendicular distance from the centre C to the line (1) is equal to the radius r.
⇔ \(\left|\frac{0-n}{\sqrt{1^{2}+m^{2}}}\right|\) = r
⇔ (n)2 = r2 (l2 + m2)
Let P(x1, y1) be the point of contact.
Equation of the tangent is S1 = 0, ⇒ x1x + y1y – r2 = 0. —- (3)
Equations (1) and (3) are representing the same line, therefore, \(\frac{x_{1}}{l}=\frac{y_{1}}{m}=\frac{-a^{2}}{n}\) ⇒ x1 = \(\frac{-a^{2} l}{n}\), y1 = \(\frac{-a^{2} m}{n}\)
Therefore, point of contact is \(\left(\frac{-a^{2} l}{n}, \frac{-a^{2} m}{n}\right)\)
Theorem: The condition for the straight line lx + my + n = 0 may be a tangent to the circle
x2 + y2 + 2gx + 2fy + c = 0 is (g2 + f2 – c) (l2 + m2) = (lg + mf – n)2.
Proof:
The given line is lx + my + n = 0 …….. (1)
The given circle is x2 + y2 + 2gx + 2fy + c = 0 …….. (2)

Centre C = (- g, – f), radius r = \(\sqrt{\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{c}}\)
Line (1) is a tangent to the circle (2)
⇔ The perpendicular distance from the centre C to the line (1) is equal to the radius r.
⇔ \(\left|\frac{-\lg -m f+c}{\sqrt{1^{2}+m^{2}}}\right|\) = \(\sqrt{\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{c}}\)
⇔ (lg + mf -n)2 = (g2 + f2 – c) (l2 + m2)
![]()
Corollary: The condition for the straight line y = mx + c to touch the circle
x2 + y2 = r2 is c2 = r2(1 + m2).
The given line is y = mx + c i.e., mx – y + c = 0 … (1)
The given circle is S = x2 + y2 = r2
Centre C = (0,0), radius = r.
If (1) is a tangent to the circle, then
Radius of the circle = perpendicular distance from centre of the circle to the line.

⇒ r = \(\frac{|c|}{\sqrt{m^{2}+1}}\) ⇒ r2 = \(\frac{c^{2}}{m^{2}+1}\) ⇒ r2 (m2 + 1) = c2
Corollary: If the straight line y = mx + c touches the circle x2 + y2 = r2, then their point of contact is \(\left(-\frac{r^{2} m}{c}, \frac{r^{2}}{c}\right)\).
Proof:
The given line is y = mx + c i.e., mx – y + c = 0 ……. (1)
The given circle is S = x2 + y2 = r2 ……. (2)
Centre C = (0, 0), radius = r
Let P(x1, y1) be the point of contact.
Equation of the tangent is S1 = 0, ⇒ x1x + y1y – r2 = 0. ………. (3)

Equations (1) and (3) are representing the same line, therefore, \(\frac{x_{1}}{m}=\frac{y_{1}}{-1}=\frac{-r^{2}}{c}\) ⇒ x1 = \(\frac{-r^{2} m}{c}\), y1 = \(\frac{r^{2}}{c}\)
Point of contact is (x1, y1) = \(\left(-\frac{\mathrm{r}^{2} \mathrm{~m}}{\mathrm{c}}, \frac{\mathrm{r}^{2}}{\mathrm{c}}\right)\)
Theorem: If P(x, y) is a point on the circle with centre C(α, β) and radius r, then x = α + r cos θ, y = β + r sin θ where 0 ≤ θ < 2π.
Note 1: The equations x = α + r cos θ, y = β + r sin θ, 0 ≤ θ < 2π are called parametric equations of the circle with centre (α, β) and radius r.
Note 2: A point on the circle x2 + y2 = r2 is taken in the form (r cosθ, r sin θ). The point (r cosθ, r sin θ) is simply denoted as point θ.
![]()
Theorem: The equation of the chord joining two points θ1 and θ2 on the circle
x2 + y2 + 2gx + 2fy + c = 0 is (x + g)cos\(\frac{\theta_{1}+\theta_{2}}{2}\) + (y + f) sin \(\frac{\theta_{1}+\theta_{2}}{2}\) = r cos \(\frac{\theta_{1}+\theta_{2}}{2}\) where r is the radius of the circle.
Note 1: The equation of the chord joining the points θ1 and θ2 on the circle x2 + y2 = r2 is x cos\(\frac{\theta_{1}+\theta_{2}}{2}\) + y sin\(\frac{\theta_{1}+\theta_{2}}{2}\) = r cos\(\frac{\theta_{1}-\theta_{2}}{2}\)
Note 2: The equation of the tangent at P(θ) on the circle (x + g) cos θ + (y + f) sin θ = \(\sqrt{g^{2}+f^{2}-c}\).
Note 3: The equation of the tangent at P(θ) on the circle x2 + y2 = r2 is x cos θ + y sin θ = r.
Note 4: The equation of the normal at P(θ) on the circle x2 + y2 = r2 is x sin θ – y cos θ = r.
Theorem:
If a line passing through a point P(x1, y1) intersects the circle S = 0 at the points A and B then PA.PB = |S11|.
Corollary:
If the two lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 meet the coordinate axes in four distinct points then those points are concyclic ⇔ a1a2 = b1b2.
Corollary:
If the lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 meet the coordinate axes in four distinct concyclic points then the equation of the circle passing through these concyclic points is (a1x + b1y + c1) (a2x + b2y + c2) – (a1b2 + a2b1)xy = 0.
![]()
Theorem:
Two tangents can be drawn to a circle from an external point.
Note:
If m1, m1 are the slopes of tangents drawn to the circle x2 + y2 = a2 from an external point (x1, y1) then m1 + m2 = \(\frac{2 x_{1} y_{1}}{x_{1}^{2}-a^{2}}\), m1m2 = \(\frac{y_{1}^{2}-a^{2}}{x_{1}^{2}-a^{2}}\).
Theorem:
If θ is the angle between the tangents through a point P to the circle S = 0 then tan = \(\frac{\theta}{2}=\frac{r}{\sqrt{S_{11}}}\) where r is the radius of the circle.
Proof:
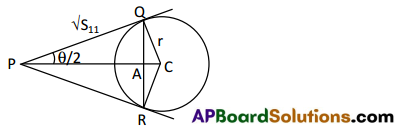
Let the two tangents from P to the circle S = 0 touch the circle at Q, R and θ be the angle between
these two tangents. Let C be the centre of the circle. Now QC = r, PQ = \(\sqrt{S_{11}}\) and ∆PQC is a right angled triangle at Q.
∴ tan \(\frac{\theta}{2}=\frac{\mathrm{QC}}{\mathrm{PQ}}=\frac{\mathrm{r}}{\sqrt{\mathrm{S}_{11}}}\)
Theorem: The equation to the chord of contact of P(x1, y1) with respect to the circle S = 0 is S1 = 0.
Theorem: The equation of the polar of the point P(x1, y1) with respect to the circle S = 0 is S1 = 0.
Theorem: The pole of the line lx + my + n = 0 (n ≠ 0) with respect to x2 + y2 = a2 is \(\left(-\frac{1 a^{2}}{n},-\frac{m a^{2}}{n}\right)\)
Proof :
Let P(x1, y1) be the pole of lx + my + n = 0 ……. (1)
The polar of P with respect to the circle is:
xx1 + yy1 – a2 = 0
Now (1) and (2) represent the same line
∴ \(\frac{\mathrm{x}_{1}}{\ell}=\frac{\mathrm{y}_{1}}{\mathrm{~m}}=\frac{-\mathrm{a}^{2}}{\mathrm{n}}\) ⇒ x1 = \(\frac{-\mathrm{la}^{2}}{\mathrm{n}}\), y1 = \(\frac{-\mathrm{ma}^{2}}{\mathrm{n}}\)
∴ Pole P = \(\left(-\frac{1 a^{2}}{n},-\frac{m a^{2}}{n}\right)\)
![]()
Theorem: If the pole of the line lx + my + n = 0 with respect to the circle x2 + y2 + 2gx + 21y + c = 0 is (x1, y1) then \(\frac{x_{1}+g}{\ell}=\frac{y_{1}+f}{m}=\frac{r^{2}}{\lg +\mathrm{mf}-\mathrm{n}}\) where r is the radius of the circle.
Proof:
Let P(x1, y1) be the pole of the line lx + my + n = 0 ……. (1)
The poiar of P with respect to S = 0 is S1 = 0
xx1 + yy1 + g(x + x1) + f(y + y1) + c = 0
⇒ (x1 + g)x + (y1 + f) + gx1 + fy1 + c = 0 …….. (2)
Now (1) and (2) represent the same line.
∴ \(\frac{\mathrm{x}_{1}+\mathrm{g}}{\ell}=\frac{\mathrm{y}_{1}+\mathrm{f}}{\mathrm{m}}=\frac{\mathrm{gx} \mathrm{x}_{1}+\mathrm{gy} \mathrm{y}_{1}+\mathrm{c}}{\mathrm{n}}\) = k(say)
\(\frac{\mathrm{x}_{1}+\mathrm{g}}{\ell}\) = k ⇒ x1 + g = l k ⇒ x1 = lk – g
\(\frac{\mathrm{y}_{1}+\mathrm{f}}{\mathrm{m}}\) = k ⇒ y1 + f = m k ⇒ y1 = mk – f
\(\frac{g x_{1}+g y_{1}+c}{n}\) = k ⇒ gx1 + gy1 + c = nk
⇒ g(lk – g) + f(mk – f) + c = nk
⇒ k (lg + mf – n) = g2 + f2 – c = r2 Where r is the radius of the circle ⇒ k = \(\frac{r^{2}}{\lg +\mathrm{mf}-\mathrm{n}}\)
∴ \(\frac{\mathrm{x}_{1}+\mathrm{g}}{\ell}=\frac{\mathrm{y}_{1}+\mathrm{f}}{\mathrm{m}}=\frac{\mathrm{r}^{2}}{\lg +\mathrm{mf}-\mathrm{n}}\)
Theorem: The lines l1x + m1y + n1 = 0 and l2x + m2y + n1y = 0 are conjugate with respect to the circle x2 + y1 + 2gx + 2fy + c = 0 iffr1 (l1l2 + m1m2) = (l1g + m1f – n1) (l2g + m2f – n2).
Theorem: The condition for the lines l1x + m1y + n1 = 0 and l2x + m2y + n2 = 0 to be conjugate with respect to the circle x2 + y2 = a2 is a2(l1l2 + m1m2) = n1n2.
Theorem: The equation of the chord of the circle S = 0 having P(x1, y1) as its midpoint is S1 = S11.
Theorem: The length of the chord of the circle S = 0 having P(x1, y1) as its midpoint is 2\(\sqrt{\left|S_{11}\right|}\).
Theorem: The equation to the pair of tangents to the circle
S = 0 from P(x1, y1) is S21 = S11S.
Proof:
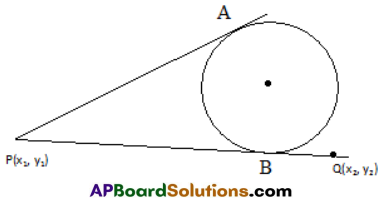
Let the tangents from P to the circle S = 0 touch the circle at A and B.
Equation of AB is S1 = 0.
i.e., x1x + y1y + g(x + x1) + f(y + y1) + c = 0 ———- (i)
Let Q(x2, y2) be any point on these tangents. Now locus of Q will be the equation of the pair of tangents drawn from P.
The line segment PQ is divided by the line AB in the ratio – S11:S22
⇒ \(\frac{P B}{Q B}=\left|\frac{S_{11}}{S_{22}}\right|\) ———— (ii)
But PB = \(\sqrt{S_{11}}\), QB = \(\sqrt{S_{22}}\) ⇒ \(\frac{P B}{Q B}=\frac{\sqrt{S_{11}}}{\sqrt{S_{22}}}\) ———— (iii)
From (ii) and (iii) ⇒ \(\frac{s_{11}^{2}}{s_{22}^{2}}=\frac{S_{11}}{S_{22}}\)
⇒ S11S22 = S212
Hence locus of Q(x2, y2) is S11S = S212
![]()
Touching Circles: Two circles S = 0 and S’ = 0 are said to touch each other if they have a unique point P in common. The common point P is called point of contact of the circles S = 0 and S’ = 0.
Circle – Circle Properties: Let S = 0, S’ = 0 be two circle with centres C1, C2 and radii r1, r2 respectively.
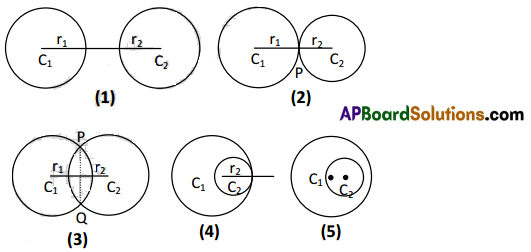
- If C1C2 > r1 + r2 then each circle lies completely outside the other circle.
- If C1C2 = r1 + r2 then the two circles touch each other externally. The point of contact divides C1C2 in the ratio r1 : r2 internally.
- If |r1 – r2| < C1C2 < r1 + r2 then the two circles intersect at two points P and Q. The chord \(\overline{\mathrm{PQ}}\) is called common chord of the circles.
- If C1C2 = |r1 – r2| then the two circles touch each other internally. The point of contact divides C1C2 in the ratio r1: r2 externally.
- If C1C1 < |r1 – r2] then one circle lies completely inside the other circle.
Common Tangents: A line L = 0 is said to be a common tangent to the circle S = 0, S’ = 0 if L = 0 touches both the circles.
Definition: A common tangent L = 0 of the circles S = 0, S’= 0 is said to be a direct common tangent of the circles if the two circles S = 0, S’ = 0 lie on the same side of L = 0.
Centres of Similitude:
Let S = 0, S’ = 0 be two circles.
- The point of intersection of direct common tangents of S = 0, S’ = 0 is called external centre of similitude.
- The point of intersection of transverse common tangents of S = 0, S’ = 0 is called internal centre of similitude.
Theorem:
Let S = 0, S’ = 0 be two circles with centres C1, C2 and radii r1, r2 respectively. If A1 and A2 are respectively the internal and external centres of similitude circles s = 0, S’ = 0 then
- A1 divides C1C2 in the ratio r1 : r2 internally.
- A2 divides C1C2 in the ratio r1 : r2 internally.