Use these Inter 1st Year Maths 1B Formulas PDF Chapter 6 Direction Cosines and Direction Ratios to solve questions creatively.
Intermediate 1st Year Maths 1B Direction Cosines and Direction Ratios Formulas
Formulae and Synopsis :
If a line PQ makes angles α, β, γ with the co – ordinate axes, then cos α, cos β, cos γ are called
direction cosines of the line PQ. We take
l = cos α, m = cos β and n = cos γ
Relation between direction cosines is l2 + m2 + n2 = 1
Direction Ratios :
An ordered triple of numbers proportional to the direction cosines of a line are defined as ‘Direction ratios’ of that fine.
→ If \(\frac{1}{a}=\frac{m}{b}=\frac{n}{c}\) then a, b, c are called direction ratios of the line.
→ If a, b, c are the direction ratios of a line, then its direction cosines are \(\left(\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}}\right)\)
→ Direction ratios of the line joining P(x1, y1, z1) and Q (x2, y2, z2) are (x2 – x1, y2 – y1, z2 – z1) or (x1 – x2, y1 – y2, z1 – z2)
→ D.cs of the above line \(\frac{x_{2}-x_{1}}{P Q}, \frac{y_{2}-y_{1}}{P Q}, \frac{z_{2}-z_{1}}{P Q}\) or \(\frac{x_{1}-x_{2}}{P Q}, \frac{y_{1}-y_{2}}{P Q}, \frac{z_{1}-z_{2}}{P Q}\)
→ Angle between the lines whose D.cs are (l1 m1, n1) and (l2, m2, n2) is given by cos θ = l1l2 + m1m2 + n1n2
→ If these lines are perpendicular, then l1l2 + m1m2 + n1n2 = 0
![]()
Angle Between Two Lines:
The angle between two skew lines is the angle between two lines drawn parallel to them through any point in space.
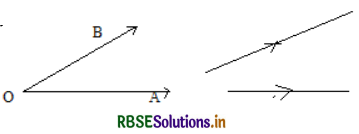
Direction Cosines:
If α, β, γ are the angles made by a directed line segment with the positive directions of the coordinate axes respectively, then cos α, cos β, cos γ are called the direction cosines of the given line and they are denoted by l, m, n respectively Thus l = cos α, m = cos β, n = cos γ
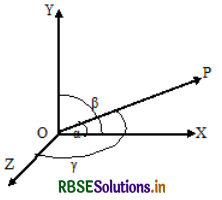
The direction cosines of \(\overline{o p}\) are l = cos α, m = cos β, n = cos γ.
If l, m, n are the d.c’s of a line L is one direction then the d.c’s of the same line in the opposite direction are -l, -m, -n.
Note :
- The angles α, β, γ are known as the direction angles and satisfy the condition 0 < α, β, γ < π.
- The sum of the angles α, β, γ is not equal to 2β because they do not lie in the same plane.
- Direction cosines of coordinate axes.
The direction cosines of the x-axis are cos0, cos\(\frac{\pi}{2}\), cos\(\frac{\pi}{2}\) i.e., 1, 0, 0
Similarly the direction cosines of the y-axis are (0, 1, 0) and z-axis are (0, 0, 1)
Theorem:
If P(x, y, z) is any point in space such that OP = r and if l, m, n are direction cosines of \(\overline{O P}\) then x = lr,y = mr, z = nr.
Note: If P(x, y, z) is any point in space such that OP = r then the direction cosines of \(\overline{O P}\) are
Note: If P is any point in space such that OP =r and direction cosines of OP are l,m,n then the point P =(lr,mr,nr)
Note: If P(x,y,z) is any point in space then the direction cosines of OP are \(\frac{x}{\sqrt{x^{2+} y^{2}+z^{2}}}, \frac{y}{\sqrt{x^{2+} y^{2}+z^{2}}}, \frac{z}{\sqrt{x^{2+} y^{2}+z^{2}}}\)
Theorem:
If l, m, n are the direction cosines of a line L then l2 + m2 + n2 = 1.
Proof:
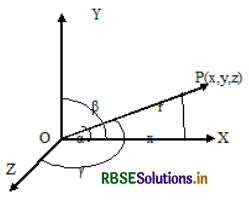
l = cos α = \(\frac{x}{r}\), m = cos β = \(\frac{y}{r}\), n = cos γ = \(\frac{z}{r}\) ⇒ cos2α + cos2β + cos2γ = \(\frac{x^{2}}{r^{2}}+\frac{y^{2}}{r^{2}}+\frac{z^{2}}{r^{2}}\)
= \(\frac{x^{2}+y^{2}+z^{2}}{r^{2}}=\frac{r^{2}}{r^{2}}\)
∴ l2 + m2 + n2 = 1
Theorem:
The direction cosines of the line joining the points P(x1, y1, z1),Q(x2, y2, z2) are
\(\left(\frac{x_{2}-x_{1}}{r}, \frac{y_{2}-y_{1}}{r}, \frac{z_{2}-z_{1}}{r}\right)\) where r = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\)
Direction Ratios:
A set of three numbers a,b,c which are proportional to the direction cosines l,m,n respectively are called DIRECTION RATIOS (d.r’s) of a line.
Note : If (a, b, c) are the direction ratios of a line then for any non-zero real number λ , (λa, λb, λc) are also the direction ratios of the same line.
Direction cosines of a line in terms of its direction ratios
If (a, b, c) are direction ratios of a line then the direction cosines of the line are ±\(\left(\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}}\right)\)
Theorem:
The direction ratios of the line joining the points are (x2 – x1, y2 – y1, z2 – z1)
![]()
Angle Between Two Lines:
If (l1, m1, n1) and (l2, m2, n2) are the direction cosines of two lines θ and is the acute angle between them, then cos θ = |l1l2 + m1m2 + n1n2|
Note.
If θ is the angle between two lines having d.c’s (l1, m1, n1) and (l2, m2, n2) then
sin θ = \(\sqrt{\sum\left(l_{1} m_{2}-l_{2} m_{1}\right)^{2}}\) and tan θ = \(\frac{\sqrt{\sum\left(l_{1} m_{2}-l_{2} m_{1}\right)^{2}}}{\left|l_{1} l_{2}+m_{1} m_{2}+n_{1} n_{2}\right|}\) where θ ≠ \(\frac{\pi}{2}\)
Note :
The condition for the lines to be perpendicular is l1l2 + m1m2 + n1n2 = 0
The condition for the lines to be parallel is \(\frac{l_{1}}{l_{2}}=\frac{m_{1}}{m_{2}}=\frac{n_{1}}{n_{2}}\)
Theorem:
If (a1, b1, c1) and (a2, b2, c2) are direction ratios of two lines and θ is the angle
between them then cos θ = \(\frac{a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\)
Note:
- If the two lines are perpendicular then a1a2 + b1b2 + c1c2 = 0
- If the two lines are parallel then \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
- If one of the angle between the two lines is 0 then other angle is 180° – θ
