Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Trigonometric Equations Solutions Exercise 7(a) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1A Trigonometric Equations Solutions Exercise 7(a)
I.
Question 1.
Find the principal solutions of the angles in the equations
(i) 2 cos2θ = 1
Solution:
cos2θ = \(\frac{1}{2}\)
θ = 45°, 135°
(ii) √3 sec θ + 2 = 0
Solution:
sec θ = \(\frac{-2}{\sqrt{3}}\)
⇒ cos θ = \(\frac{-\sqrt{3}}{2}\)
⇒ θ = 150°
(iii) 3 tan2θ = 1
Solution:
tan2θ = \(\frac{1}{3}\)
θ = ±\(\frac{\pi}{6}\)
![]()
Question 2.
Solve the following equations.
(i) cos 2θ = \(\frac{\sqrt{5}+1}{4}\), θ ∈ [0, 2π]
Solution:
cos 2θ = \(\frac{\sqrt{5}+1}{4}\)
⇒ cos 2θ = cos 36° = cos (\(\frac{\pi}{5}\))
and \(\frac{\pi}{5}\) ∈ [0, 2π]
2θ = \(\frac{\pi}{5}\) ⇒ θ = \(\frac{\pi}{10}\) is the principal solution
and 2θ = 2nπ ± \(\frac{\pi}{5}\) where n ∈ Z is the general solution
⇒ θ = nπ ± \(\frac{\pi}{10}\)
The values of θ in [0, 2π] are \(\left\{\frac{\pi}{10}, \frac{9 \pi}{10}, \frac{11 \pi}{10}, \frac{19 \pi}{10}\right\}\)
(ii) tan2θ = 1, θ ∈ [-π, π]
Solution:
tan2θ = 1 ⇒ tan θ = ±1
tan θ = ±1 = tan (\(\pm \frac{\pi}{4}\))
The principal solutions are θ = \(\pm \frac{\pi}{4}\)
and the general solution is given by nπ ± \(\frac{\pi}{4}\), n ∈ Z
Put n = -1, 0, 1
\(\left\{\frac{-3 \pi}{4}, \frac{-\pi}{4}, \frac{\pi}{4}, \frac{3 \pi}{4}\right\}\) is the solution set for the given equation in [-π, π]
(iii) sin 3θ = \(\frac{\sqrt{3}}{2}\), θ ∈ [-π, π]
Solution:
sin 3θ = \(\frac{\sqrt{3}}{2}\) = sin \(\frac{\pi}{3}\)
and \(\frac{\pi}{3}\) ∈ [-π, π]
∴ 3θ = \(\frac{\pi}{3}\) is the principal solution
and 3θ = \(n \pi+(-1)^{n} \frac{\pi}{3}\), n ∈ Z
⇒ θ = \(\frac{n \pi}{3}+(-1)^{n} \cdot \frac{\pi}{9}\), n ∈ Z is the general solution.
The solution of θ in [-π, π] are \(\left\{\frac{-5 \pi}{9}, \frac{-4 \pi}{9}, \frac{\pi}{9}, \frac{2 \pi}{9}, \frac{7 \pi}{9}, \frac{8 \pi}{9}\right\}\)
(iv) cos2θ = \(\frac{3}{4}\), θ ∈ [0, π]
Solution:
cos2θ = \(\frac{3}{4}\)
⇒ cos θ = ±\(\frac{\sqrt{3}}{4}\)
The general solution is given by
θ = nπ ± \(\frac{\pi}{6}\), n ∈ Z
Put n = 0, 1
The solution set for the given equation in [0, π] is \(\left\{\frac{\pi}{6}, \frac{5 \pi}{6}\right\}\)
(v) 2 sin2θ = sin θ, θ ∈ (0, π)
Solution:
2 sin2θ – sin θ = 0
sin θ (2 sin θ – 1) = 0
sin θ = 0 or sin θ = \(\frac{1}{2}\)
since θ ∈ (0, π)
∴ The solution of θ = \(\left\{\frac{\pi}{6}+\frac{5 \pi}{6}\right\}\)
![]()
Question 3.
Find general solutions to the following equations.
(i) sin θ = \(\frac{\sqrt{3}}{2}\), cos θ = \(\frac{-1}{2}\)
Solution:
sin θ = \(\frac{\sqrt{3}}{2}\), cos θ = \(\frac{-1}{2}\)
∵ sin θ is +ve and cos θ is -ve
⇒ θ lies in II quadrant
sin θ = \(\frac{\sqrt{3}}{2}=\sin \left(\frac{2 \pi}{3}\right)\)
cos θ = \(\frac{-1}{2}=\cos \left(\frac{2 \pi}{3}\right)\)
⇒ θ = 2nπ ± \(\frac{2 \pi}{3}\), n ∈ Z is the general solution.
(ii) tan x = \(\frac{-1}{\sqrt{3}}\), sec x = \(\frac{2}{\sqrt{3}}\)
Solution:
∵ tan x = \(\frac{-1}{\sqrt{3}}\) and sec x = \(\frac{2}{\sqrt{3}}\)
⇒ x lies in IV quadrant
tan x = \(\frac{-1}{\sqrt{3}}=\tan \left(\frac{-\pi}{6}\right)\)
sec x = \(\frac{2}{\sqrt{3}}=\sec \left(\frac{-\pi}{6}\right)\)
∴ θ = 2nπ + \(\left(\frac{-\pi}{6}\right)\), n ∈ Z is the general solution.
(iii) cosec θ = -2, cot θ = -√3
Solution:
cosec θ = -2, cot θ = -√3
⇒ θ lies in IV quadrant
cosec θ = -2
⇒ sin θ = \(-\frac{1}{2}=\sin \left(-\frac{\pi}{6}\right)\)
cot θ = -√3
⇒ tan θ = \(-\frac{1}{\sqrt{3}}=\tan \left(-\frac{\pi}{6}\right)\)
∴ θ = 2nπ + \(\left(\frac{-\pi}{6}\right)\), n ∈ Z is the general solution.
Question 4.
(i) If sin (270° – x) = cos 292°, then find x in (0, 360°).
Solution:
sin (270° – x) = cos (292°)
⇒ -cos x = cos (180° + 112°)
⇒ -cos x = -cos 112°
⇒ cos x = cos 112°
⇒ x = 112° or x = 360° – 112° = 248°
(ii) If x < 90°and sin (x + 28°) = cos (3x – 78°), then find x.
Solution:
sin (x + 28°) = cos (3x – 78°)
= sin (90° – 3x + 78°)
= sin (168° – 3x)
x + 28° = 168° – 3x + 28° (180°) or
= 180° – (168° – 3x) + 2x (180°)
⇔ there exists n ∈ Z such that
4x = 140° + 2x (180°)
2x = 16° – 2x (180°)
⇔ there exists n ∈ z such that
x = 35° + x(90°) or x = 8° – x (180°)
Hence x = 8° and x = 35° are the only values of x that lie (0, 90°) and satisfy the given equation.
![]()
Question 5.
Find general solutions to the following equations.
(i) 2 sin2θ = 3 cos θ
Solution:
2 sin2θ = 3 cos θ
⇒ 2(1 – cos2θ) = 3 cos θ
⇒ 2 cos2θ + 3 cos θ – 2 = 0
⇒ 2 cos2θ + 4 cos θ – cos θ – 2 = 0
⇒ 2 cos θ (cos θ + 2) – 1 (cos θ + 2) = 0
⇒ (2 cos θ – 1) (cos θ + 2) = 0
⇒ cos θ = \(\frac{1}{2}\) (or) cos θ = -2
∴ The range of cos θ is [-1, 1]
cos θ = -2 is not admissible
∴ cos θ = \(\frac{1}{2}=\cos \frac{\pi}{3}\)
⇒ θ = \(\frac{\pi}{3}\) is the principal solution and
θ = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z is the general solution.
(ii) sin2θ – cos θ = \(\frac{1}{4}\)
Solution:
sin2θ – cos θ = \(\frac{1}{4}\)
⇒ 4(1 – cos2θ) – 4 cos θ = 1
⇒ 4 cos2θ + 4 cos θ – 3 = 0
⇒ 4 cos2θ + 6 cos θ – 2 cos θ – 3 = 0
⇒ 2 cos θ (2 cos θ + 3) – (2 cos θ + 3) = 0
⇒ (2 cos θ – 1) (2 cos θ + 3) = 0
∴ cos θ = \(\frac{1}{2}\) (or) cos θ = \(\frac{-3}{2}\)
∵ The range of cos θ is [-1, 1]
cos θ = \(\frac{-3}{2}\) is not admisable
∴ cos θ = \(\frac{1}{2}=\cos \left(\frac{\pi}{3}\right)\)
θ = \(\frac{\pi}{3}\) is the principal solution and
θ = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z is the general solution.
(iii) 5 cos2θ + 7 sin2θ = 6
Solution:
5 cos2θ + 7 sin2θ = 6
Dividing by cos2θ
⇒ 5 + 7 tan2θ = 6 sec2θ
⇒ 5 + 7 tan2θ = 6(1 + tan2θ)
⇒ tan2θ = 1
⇒ tan θ = ±1
∴ θ = nπ ± \(\frac{\pi}{4}\), n ∈ Z is the general solution.
(iv) 3 sin4x + cos4x = 1
Solution:
3 sin4x + cos4x = 1
⇒ 3 sin4x + (cos2x)2 = 1
⇒ 3 sin4x + (1 – sin2x)2 = 1
⇒ 3 sin4x + 1 + sin4x – 2 sin2x = 1
⇒ 4 sin4x – 2 sin2x = 0
⇒ 2 sin2x (2 sin2x – 1) = 0
⇒ sin x = 0 (or) sin x = ±\(\frac{1}{\sqrt{2}}\)
If sin x = 0
⇔ x = nπ, n ∈ Z is the general solution.
If sin x = ±\(\frac{1}{\sqrt{2}}\)
⇒ x = nπ ± \(\frac{\pi}{4}\), n ∈ Z is the general solution.
∴ General solution is x = nπ (or) nπ ± \(\frac{\pi}{4}\), n ∈ Z.
![]()
II.
Question 1.
Solve the following equations and write a general solution.
(i) 2 sin2θ – 4 = 5 cos θ
Solution:
2(1 – cos2θ) – 4 = 5 cos θ
2 – 2cos2θ – 4 = 5 cos θ
2 cos2θ + 5 cos θ + 2 = 0
2 cos2θ + 4 cos θ + cos θ + 2 = 0
2 cos θ (cos θ + 2) + 1 (cos θ + 2) = 0
(cos θ + 2) (2 cos θ + 1) = 0
cos θ = -2 or cos θ = \(-\frac{1}{2}\)
cos θ = -2 is not possible
∴ cos θ = \(-\frac{1}{2}\) = cos \(\frac{2 \pi}{3}\)
∴ General solution is θ = 2nπ ± \(\frac{2 \pi}{3}\), n ∈ Z
(ii) 2 + √3 sec x – 4 cos x = 2√3
Solution:
2 + √3 sec x – 4 cos x = 2√3
\(\frac{2 \cos x+\sqrt{3}-4 \cos ^{2} x}{\cos x}\) = 2√3
2 cos x + √3 – 4 cos2x = 2√3 cos x
4 cos2x + 2√3 cos x – 2 cos x – √3 = 0
2 cos x (2 cos x + √3) – 1 (2 cos x + √3) = 0
(2 cos x – 1) (2 cos x + √3) = 0
cos x = \(\frac{1}{2}\) (or) cos x = \(\frac{-\sqrt{3}}{2}\)
If cos x = \(\frac{1}{2}\) = cos \(\frac{\pi}{3}\), n ∈ Z
General solution x = 2nπ ± \(\frac{\pi}{3}\)
If cos x = \(\frac{-\sqrt{3}}{2}\) = cos \(\frac{5 \pi}{3}\)
General solution x = 2nπ ± \(\frac{5 \pi}{3}\), n ∈ Z
(iii) 2 cos2θ + 11 sin θ = 7
Solution:
2 (1 – sin2θ) + 11 sin θ = 7
2 – 2 sin2θ + 11 sin θ = 7
2 sin2θ – 11 sin θ + 5 = 0
2 sin2θ – 10 sin θ – sin θ + 5 = 0
2 sin θ (sin θ – 5) – 1(sin θ – 5) = 0
(sin θ – 5) (2 sin θ – 1) = 0
sin θ = 5 or sin θ = \(\frac{1}{2}\)
If sin θ = 5 is not possible
∴ sin θ = \(\frac{1}{2}\) = sin \(\frac{\pi}{6}\)
General solultion θ = nπ + (-1)n \(\frac{\pi}{6}\), n ∈ Z
![]()
(iv) 6 tan2x – 2 cos2x = cos 2x
Solution:
6 tan2x – 2 cos2x = cos 2x
⇒ 6(sec2x – 1) – 2 cos2x = 2 cos2x – 1
⇒ 6 sec2x – 6 – 4 cos2x + 1 = 0
⇒ 6 sec2x – 4 cos2x – 5 = 0
⇒ \(\frac{6}{\cos ^{2} x}\) – 4 cos2x – 5 = 0
⇒ 6 – 4 cos4x – 5 cos2x = 0
⇒ 4 cos4x + 5 cos2x – 6 = 0
⇒ 4 cos4x + 8 cos2x – 3 cos2x – 6 = 0
⇒ 4 cos2x (cos2x + 2) – 3(cos2x + 2) = 0
⇒ (4 cos2x – 3) (cos2x + 2) = 0
⇒ 4 cos2x = 3, cos2x ≠ -2
⇒ cos x = ±\(\frac{\sqrt{3}}{2}\)
∴ x = nπ ± \(\frac{\pi}{6}\), n ∈ Z is the general solution.
(v) 4 cos2θ + √3 = 2(√3 + 1) cos θ
Solution:
4 cos2θ – 2(√3 + 1) cos θ + √3 = 0
⇒ 4 cos2θ – 2√3 cos θ – 2 cos θ + √3 = 0
⇒ 2 cos θ (2 cos θ – √3) – 1(2 cos θ – √3) = 0
⇒ (2 cos θ – 1) (2 cos θ – √3) = 0
⇒ cos θ = \(\frac{1}{2}\) (or) cos θ = \(\frac{\sqrt{3}}{2}\)
If cos θ = \(\frac{1}{2}\) = cos \(\left(\frac{\pi}{3}\right)\)
∴ θ = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z is the general solution.
If cos θ = \(\frac{\sqrt{3}}{2}\) = cos \(\left(\frac{\pi}{6}\right)\)
∴ θ = 2nπ ± \(\frac{\pi}{6}\), n ∈ Z is the general solution.
(vi) 1 + sin 2x – (sin 3x – cos 3x)2
Solution:
1 + sin 2x = (sin 3x – cos 3x)2
⇒ 1 + sin 2x = sin23x + cos23x – 2 sin 3x cos 3x
⇒ 1 + sin 2x = 1 – sin (2 × 3x)
⇒ sin 6x + sin 2x = 0
⇒ \(2 \sin \left(\frac{6 x+2 x}{2}\right) \cdot \cos \left(\frac{6 x-2 x}{2}\right)=0\)
⇒ sin (4x) . cos (2x) = 0
⇒ cos 2x = 0 (or) sin 4x = 0
If cos 2x = 0 = cos \(\frac{\pi}{2}\)
⇒ 2x = \(\frac{\pi}{2}\) is the principal solution and
2x = (2n + 1) \(\frac{\pi}{2}\), n ∈ Z is the general solution,
so that x = \(\frac{n \pi}{2}+\frac{\pi}{4}\), n ∈ Z
If sin 4x = 0 = sin(nπ), n ∈ Z
4x = nπ, n ∈ Z is the general solution.
So that 4x = nπ
⇒ x = \(\frac{n \pi}{4}\), n ∈ Z
∴ x = \(\frac{n \pi}{4}\); \(\frac{n \pi}{2}+\frac{\pi}{4}\), n ∈ Z is the general solution.
(vii) 2 sin2x + sin22x = 2
Solution:
2 sin2x + sin2(2x) = 2
⇒ 2 sin2x + (2 sin x cos x)2 – 2 = 0
⇒ sin2x + 2 sin2x cos2x – 1 = 0
⇒ 2 sin2x cos2x – (1 – sin2x) = 0
⇒ 2 sin2x cos2x – cos2x = 0
⇒ cos2x (2 sin2x – 1) = 0
⇒ cos x = 0 (or) sin x = ±\(\frac{1}{\sqrt{2}}\)
If cos x = 0 = cos \(\frac{\pi}{2}\)
⇒ x = \(\frac{\pi}{2}\) is the principal solution
and cos x = 0 ⇔ \(\sin \left(x-\frac{\pi}{2}\right)=0\)
⇔ x – \(\frac{\pi}{2}\) = nπ, n ∈ Z
⇔ x = nπ + \(\frac{\pi}{2}\)
⇔ x = (2n + 1) \(\frac{\pi}{2}\), n ∈ Z
∴ x = (2n + 1) \(\frac{\pi}{2}\), n ∈ Z is the general solution of cos x = 0
If sin x = ±\(\frac{1}{\sqrt{2}}\) = sin(±\(\frac{\pi}{4}\))
x = ±\(\frac{\pi}{4}\) are principal solutions
and x = nπ ± \(\frac{\pi}{4}\), n ∈ Z is the general solution
∴ The general solutions are \(\left[\left\{(2 n+1) \frac{\pi}{2}\right\},\left\{n \pi \pm \frac{\pi}{4}\right\} n \in Z\right]\)
![]()
Question 2.
Solve the following equations.
(i) √3 sin θ – cos θ = √2
Solution:

(ii) cot x + cosec x = √3
Solution:
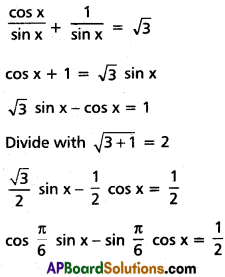

(iii) sin x + √3 cos x = √2
Solution:

Question 3.
Solve the following equations:
(i) tan θ + sec θ = √3, 0 ≤ θ ≤ 2π
Solution:


(ii) cos 3x + cos 2x = sin \(\frac{3 x}{2}\) + sin \(\frac{x}{2}\), 0 ≤ x ≤ 2π
Solution:


(iii) cot2x – (√3 + 1) cot x + √3 = 0, 0 < x < \(\frac{\pi}{2}\)
Solution:
cot2x – (√3 + 1) cot x + √3 = 0
⇔ cot2x – √3 cot x – cot x + √3 = 0
⇔ cot x (cot x – √3) – 1(cot x – √3) = 0
⇔ cot x = √3 (or) cot x = 1
case (i): cot x = 1 ⇒ tan x = 1
∴ x = \(\left\{\frac{\pi}{4}\right\}\)
case (ii): cot x = √3 ⇒ tan x = \(\frac{1}{\sqrt{3}}\)
∴ x = \(\left\{\frac{\pi}{6}\right\}\)
∴ Solutions are \(\left\{\frac{\pi}{6}, \frac{\pi}{4}\right\}\)
![]()
(iv) sec x . cos 5x + 1 = 0; 0 < x < 2π
Solution:

III.
Question 1.
(i) Solve sin x + sin 2x + sin 3x = cos x + cos 2x + cos 3x
Solution:
(sin 3x + sin x) + sin 2x = (cos 3x + cos x) + cos 2x
⇔ 2 . sin(\(\frac{3 x+x}{2}\)) . cos (\(\frac{3 x-x}{2}\)) + sin 2x = 2 . cos (\(\frac{3 x+x}{2}\)) . cos (\(\frac{3 x-x}{2}\)) + cos 2x
⇔ 2 sin 2x cos x + sin 2x = 2 cos 2x cos x + cos 2x
⇔ sin 2x (2 cos x + 1) = cos 2x (2 cos x + 1)
⇔ (2 cos x + 1) (sin 2x – cos 2x ) = 0
⇔ cos x = \(-\frac{1}{2}\) (or) sin 2x = cos 2x (i.e.,) tan (2x) = 1
Case (i):
cos x = \(-\frac{1}{2}\) = cos (\(\frac{2 \pi}{3}\))
Principal solution is x = \(\frac{2 \pi}{3}\)
and General solution is x = 2nπ ± \(\frac{2 \pi}{3}\), n ∈ z
Case (ii):
tan 2x = 1 = tan \(\frac{\pi}{4}\)
∴ Principal solution is 2x = \(\frac{\pi}{4}\) (i.e.,) x = \(\frac{\pi}{2}\)
General solution is 2x = nπ + \(\frac{\pi}{4}\), n ∈ z
⇒ x = \(\frac{\mathrm{n} \pi}{2}+\frac{\pi}{8}\), n ∈ Z
∴ General solution is \(\left.\left[\left\{2 n \pi \pm \frac{2 \pi}{3}\right\},\left\{\frac{n \pi}{2}+\frac{\pi}{8}\right\} / n \in Z\right\}\right]\)
(ii) If x + y = \(\frac{2 \pi}{3}\) and sin x + sin y = \(\frac{3}{2}\), find x and y.
Solution:

(iii) If sin 3x + sin x + 2 cos x = sin 2x + 2 cos2x, find the general solution.
Solution:
Given sin 3x + sin x + 2 cos x = sin 2x + 2 cos2x
⇒ 2 . sin (\(\frac{3 x+x}{2}\)) . cos (\(\frac{3 x-x}{2}\)) + 2 cos x = 2 sin x cos x + 2 cos2x
⇒ 2 . sin 2x . cos x + 2 cos x = 2 cos x (sin x + cos x)
⇒ 2 cos x (sin 2x + 1) = 2 cos x (sin x + cos x)
⇒ 2 cos x [sin 2x + 1 – sin x – cos x] = 0
⇒ cos x = 0 (or) sin 2x – sin x + 1 – cos x = 0


(iv) Solve cos 3x – cos 4x = cos 5x – cos 6x
Solution:
-2 sin 5x . sin x = -2 sin 4x . sin x
⇒ 2 sin x [sin 5x – sin 4x] = 0
⇒ 4 sin x . cos \(\frac{9 x}{2}\) . sin \(\frac{x}{2}\) = 0
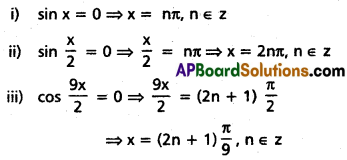
Question 2.
Solve the following equations.
(i) cos 2θ + cos 8θ = cos 5θ
Solution:
cos 2θ + cos 8θ = cos 5θ
2 cos (\(\frac{2 \theta+8 \theta}{2}\)) cos (\(\frac{2 \theta-8 \theta}{2}\)) – cos 5θ = 0
2 cos 5θ . cos 3θ – cos 5θ = 0
cos 5θ (2 cos 3θ – 1) = 0
If cos 5θ = 0
Solution is 5θ = (2n + 1) \(\frac{\pi}{2}\)
θ = (2n + 1) \(\frac{\pi}{10}\), n ∈ z
If 2 cos 3θ – 1 = 0
cos 3θ = \(\frac{1}{2}\) = cos \(\frac{\pi}{3}\)
Solution is 3θ = 2nπ ± \(\frac{\pi}{3}\)
θ = \(\frac{2 n \pi}{3} \pm \frac{\pi}{9}\), n ∈ Z
(ii) cos θ – cos 7θ = sin 4θ
Solution:
-2 sin (\(\frac{\theta+7 \theta}{2}\)) sin (\(\frac{\theta-7 \theta}{2}\)) – sin 4θ = 0
2 sin 4θ sin 3θ – sin 4θ = 0
sin 4θ (2 sin 3θ – 1) = 0
If sin 4θ = 0
∴ Solution is 4θ = nπ
θ = \(\frac{n \pi}{4}\), n ∈ z
If 2 sin 3θ – 1 = 0
sin 3θ = \(\frac{1}{2}\) = sin \(\frac{\pi}{6}\)
Solution is 3θ = nπ + (-1)n \(\frac{\pi}{6}\)
θ = \(\frac{n \pi}{3}+(-1)^{n} \frac{\pi}{18}\), n ∈ z
![]()
(iii) sin θ + sin 5θ = sin 3θ, 0 < θ < π
Solution:
sin θ + sin 5θ = sin 3θ
sin θ + sin 5θ – sin 3θ = 0
sin θ + 2 cos (\(\frac{5 \theta+3 \theta}{2}\)) sin (\(\frac{5 \theta-3 \theta}{2}\)) = 0
sin θ + 2 cos 4θ . sin θ = 0
sin θ (1 + 2 cos 4θ) = 0
sin θ = 0, cos 4θ = \(\frac{-1}{2}\)
If sin θ = 0, solution is θ = nπ, n ∈ Z
If cos 4θ = \(\frac{-1}{2}\) = cos(\(\frac{2 \pi}{3}\))
Solution is 4θ = 2nπ ± \(\frac{2 \pi}{3}\)
θ = \(\frac{2 n \pi}{4} \pm \frac{2 \pi}{12}\), n ∈ Z
θ = \(\frac{n \pi}{2} \pm \frac{\pi}{6}\), n ∈ Z
Since 0 < θ < π
Then π = \(\frac{\pi}{6}, \frac{\pi}{3}, \frac{2 \pi}{3}, \frac{5 \pi}{6}\)
Question 3.
(i) If tan pθ = cot qθ and p ≠ -q show that the solutions are in A.P. with common difference \(\frac{\pi}{p+q}\)
Solution:
tan pθ = cot qθ = tan \(\frac{\pi}{2}\) – qθ
pθ = nπ + \(\frac{\pi}{2}\) – qθ
(p + q) θ = (2n + 1) \(\frac{\pi}{2}\)
θ = \(\frac{(2 n+1)}{p+q} \frac{\pi}{2}\), n is an integer
The Solutions \(\frac{\pi}{2(p+q)}, \frac{3 \pi}{2(p+q)}, \frac{5 \pi}{2(p+q)}\) + …………
∴ The solution form an Arithematical proportion With common difference \(\frac{2 \pi}{2(p+q)}=\frac{\pi}{p+q}\)
(ii) Show that the solutions of cos pθ = sin qθ form two series each of which is an A.P. Find also the common difference of each A.P. (p ≠ ±q).
Solution:
cos pθ = sin qθ
cos pθ – sin qθ = 0
cos pθ + \(\cos \left[\frac{\pi}{2}+9 \theta\right]\) = 0

(iii) Find the number of solutions of the equation tan x + sec x = 2 cos x; cos x ≠ 0, lying in the interival (0, π).
Solution:
tan x + sec x = 2 cos x
\(\frac{\sin x}{\cos x}+\frac{1}{\cos x}\) = 2 cos x
sin x + 1 = 2 cos2x
sin x + 1 = 2(1 – sin2x)
sin x + 1 = (2 – 2 sin2x)
2 sin2x + sin x – 1 = 0
2 sin2x + 2 sin x – sin x – 1 = 0
2 sin x (sin x + 1) – 1 (sin x + 1) = 0
(sin x + 1)(2 sin x – 1) = 0
sin x = -1 (or) sin x = \(\frac{1}{2}\)
If sin x = -1
x = \(\frac{-\pi}{2} \text { (or) } \frac{3 \pi}{2}\)
If sin x = \(\frac{1}{2}\)
x = \(\frac{\pi}{6} \text { (or) } \frac{5 \pi}{6}\)
In the interval (0, π)
Number of solutions = 2
(iv) Solve sin 3α = 4 sin α sin(x + α) sin(x – α) where α ≠ nπ, n ∈ Z
Solution:
3 sin α – 4 sin3α = 4 sin α (sin2x – sin2α)
Dividing with sin α
3 – 4 sin2α = 4 (sin2x – sin2α)
3 – 4 sin2α = 4 sin2x – 4 sin2α
4 sin2x = 3
2 sin2x = \(\frac{3}{2}\)
1 – cos 2x = \(\frac{3}{2}\)
cos 2x = \(-\frac{1}{2}=\cos \frac{2 \pi}{3}\)
2x = 2nπ ± \(\frac{2 \pi}{3}\), ∀ n ∈ Z
x = nπ ± \(\frac{\pi}{3}\), n ∈ Z
![]()
Question 4.
(i) If tan(π cos θ) = cot(π sin θ), then prove that \(\cos \left(\theta-\frac{\pi}{4}\right)=\pm \frac{1}{2 \sqrt{2}}\)
Solution:

(ii) Find the range of θ if cos θ + sin θ is positive.
Solution:
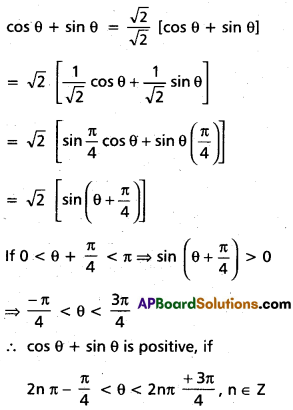
Question 5.
If α, β are the solutions of the equation a cos θ + b sin θ = c, where a, b, c ∈ R and if a2 + b2 > 0, cos α ≠ cos β and sin α ≠ sin β, then show that
(i) sin α + sin β = \(\frac{2 b c}{a^{2}+b^{2}}\)
(ii) cos α + cos β = \(\frac{2 a c}{a^{2}+b^{2}}\)
(iii) cos α . cos β = \(\frac{c^{2}-b^{2}}{a^{2}+b^{2}}\)
(iv) sin α . sin β = \(\frac{c^{2}-a^{2}}{a^{2}+b^{2}}\)
Solution:
a cos θ = b sin θ = c
First write this as a quadratic equation in sin θ
⇔ a cos θ = c – b sin θ
By squaring on both sides, we get
a2 cos2θ = (c – b sin θ)2
⇔ a2 (1 – sin2θ) = c2 + b2 sin2θ – 2 bc sin θ
⇔ (a2 + b2) sin2θ – 2bc sin θ + (c2 – a2) = 0
It is a quadratic equation in sin θ,
It has sin α and sin β as roots since α and β are solutions for the given equation
(i) Sum of the roots = sin α + sin β = \(\frac{2 b c}{a^{2}+b^{2}}\)
Again a cos θ + b sin θ = c
Write this as a quadratic equation in cos θ
⇔ b sin θ = c – a cos θ
By squaring on both sides
⇔ b2 sin2θ = (c – a cos θ)2
⇔ b2(1 – cos2θ) = c2 + a2 cos2θ – 2 ca cos θ
⇔ (a2 + b2) cos2θ – 2 ca cos θ + (c2 – b2) = 0
It is a quadratic equation in cos θ. It has cos α, cos β be its roots.
(ii) Sum of the roots = cos α + cos β = \(\frac{2 c a}{a^{2}+b^{2}}\)
(iii) Product of the roots = cos α . cos β = \(\frac{c^{2}-b^{2}}{a^{2}+b^{2}}\)
(iv) Product of the roots = sin α . sin β = \(\frac{c^{2}-a^{2}}{a^{2}+b^{2}}\)
![]()
Question 6.
(i) Find the common roots of the equations cos 2x + sin 2x = cot x and 2 cos2x + cos22x = 1.
Solution:
Let tan x = A
Given that cos 2x + sin 2x = cot x
⇔ \(\frac{1-\tan ^{2} x}{1+\tan ^{2} x}+\frac{2 \tan x}{1+\tan ^{2} x}=\frac{1}{\tan x}\)
⇔ \(\frac{1-A^{2}}{1+A^{2}}+\frac{2 A}{1+A^{2}}=\frac{1}{A}\)
⇔ (1 – A2 + 2A) A = (1 + A2)
⇔ A – A3 + 2A2 = 1 + A2
⇔ A3 – A2 – A + 1 = 0
⇔ A = 1
A = 1 satisfy this equation

∴ A3 – A2 – A + 1 = 0
⇔ (A – 1) (A2 – 1) = 0
⇔ (A – 1) (A – 1) (A + 1) = 0
⇔ A = 1, A = -1
∴ tan x = ±1
⇒ x = (2n + 1) \(\frac{\pi}{4}\), n ∈ z
Given 2 cos2x + cos2 2x = 1
⇔ (2 cos2x – 1) + cos2(2x) = 0
⇔ cos 2x + cos2(2x) = 0
⇔ cos 2x (1 + cos 2x) = 0
⇔ cos 2x = 0 (or) cos 2x = -1
Case (i): cos 2x = 0
⇔ 2x = (2n + 1) \(\frac{\pi}{2}\)
∴ x = (2n + 1) \(\frac{\pi}{4}\), n ∈ z
∴ (2n + 1) \(\frac{\pi}{4}\), n ∈ z is the common root for the given two trigonometric equations.
(ii) Solve the equation \(\sqrt{6-\cos x+7 \sin ^{2} x}+\cos x=0\)
Solution:
\(\sqrt{6-\cos x+7 \sin ^{2} x}+\cos x=0\)
6 – cos x + 7 sin2x ≥ 0
⇒ 7(1 – cos2x) – cos x + 6 ≥ 0
⇒ 7 – 7 cos2x – cos x + 6 ≥ 0
⇒ 7 cos2x + cos x – 13 ≤ 0
Consider 7 cos2x + cos x – 13 = 0
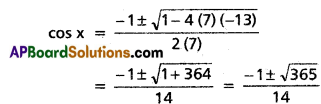
cos x values do not lie in [-1, 1]
Hence the given equation has no solution.
(iii) If |tan x| = tan x + \(\frac{1}{\cos x}\) and x ∈ [0, 2π], find the value of x.
Solution:
Case (i):
|tan x| = tan x, if x lies either in I (or) in III quadrant
Then |tan x| = tan x + \(\frac{1}{\cos x}\)
⇒ tan x = tan x + sin x
⇒ sec x = 0 which is impossible, since sec x ∉ (-1, 1)
Case (ii):
|tan x| = -tan x, if x lies in II & IV quadrants
Then |tan x| = tan x + \(\frac{1}{\cos x}\)
⇒ -tan x = tan x + sec x
⇒ -2 tan x = sec x
⇒ \(-2 \frac{\sin x}{\cos x}-\frac{1}{\cos x}\) = 0
⇒ -2 sin x – 1 = 0
⇒ sin x = \(\frac{-1}{2}=\sin \left(\frac{-\pi}{6}\right)=\sin \left(2 \pi-\frac{\pi}{6}\right)\)
∴ x = \(\frac{11 \pi}{6}\)