AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 3 Polynomials Ex 3.2 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 3rd Lesson Polynomials Exercise 3.2
10th Class Maths 3rd Lesson Polynomials Ex 3.2 Textbook Questions and Answers
Question 1.
The graphs of y = p(x) are given in the figure below, for some polynomials p(x). In each case, find the number of zeroes of p(x).
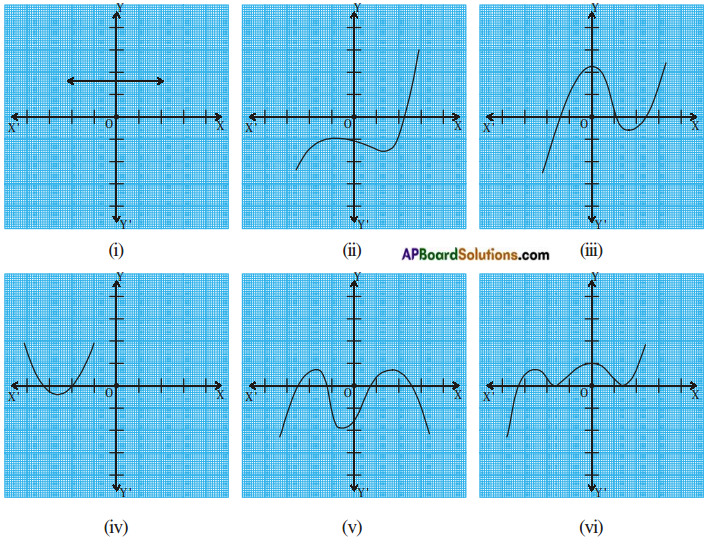
Answer:
i) There are no zeroes as the graph does not intersect the X – axis.
ii) The number of zeroes is one as the graph intersects the X – axis at one point only.
iii) The number of zeroes is three as the graph intersects the X – axis at three points.
iv) The number of zeroes is two as the graph intersects the X – axis at two points.
v) The number of zeroes is four as the graph intersects the X – axis at four points.
vi) The number of zeroes is three as the graph intersects the X – axis at three points.
![]()
Question 2.
Find the zeroes of the given polynomials,
(i) p(x) = 3x
(ii) p(x) = x2 + 5x + 6
(iii) p(x) = (x + 2) (x + 3)
(iv) p(x) = x4 – 16
Answer:
i) Given p(x) = 3x
Let p(x) = 0
So, 3x = 0
x = \(\frac{0}{3}\) = 0,
Zeroes of p(x) = 3x is zero.
∴ No. of zeroes is one.
ii) Given p(x) = x2 + 5x + 6 is a quadratic polynomial.
It has atmost two zeroes.
To find zeroes, let p(x) = 0
⇒ x2 + 5x + 6 = 0
⇒ x2 + 3x + 2x + 6 = 0
⇒ x(x + 3) + 2 (x + 3) = 0
⇒ (x + 3) (x + 2) = 0
⇒ x + 3 = 0 or x + 2 = 0
⇒ x = -3 or x = -2
Therefore the zeroes of the polynomial are -3 and -2.
iii) Given p(x) = (x + 2) (x + 3)
It is a quadratic polynomial.
It has atmost two zeroes.
Let p(x) = 0
⇒ (x + 2) (x + 3) = 0
⇒ (x + 2) = 0 or (x + 3) = 0
⇒ x = -2 or x = -3
Therefore the zeroes of the polynomial are -2 and – 3.
iv) Given p(x) = x4 – 16 is a biquadratic polynomial. It has atmost two zeroes.
Let p(x) = 0
⇒ x4 – 16 = 0
⇒ (x2)2 – 42 = 0
⇒ (x2 – 4) (x2 + 4) = 0
⇒ (x + 2) (x – 2) (x2 + 4) = 0
⇒ (x + 2) = 0 or (x – 2) = 0 or (x2 + 4) = 0
⇒ x = -2 (or) x = 2 (or) x2 = -4
Therefore the zeroes of the polynomial are 2, – 2, we do not consider √-4 since it is not real.
![]()
Question 3.
Draw the graphs of the given polynomial and find the zeroes. Justify the answers,
i) p(x) = x2 – x – 12
ii) p(x) = x2 – 6x + 9
iii) p(x) = x2 – 4x + 5
iv) p(x) = x2 + 3x – 4
v) p(x) = x2 – 1
Answer:
i) Given polynomial p(x) = x2 – x – 12.
List of values of p(x):

Now, let’s locate the points listed above on a graph paper and draw the graph.
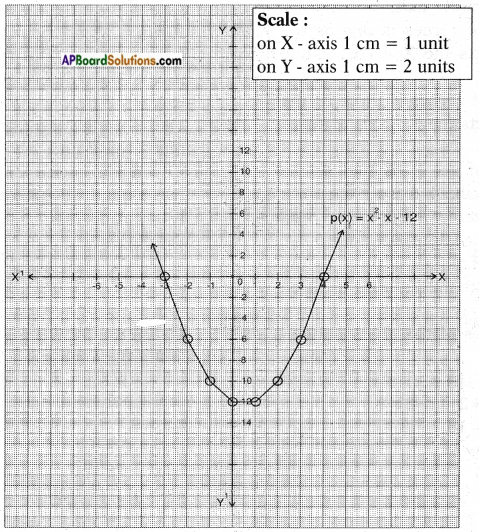
Result: We observe that the graph cuts the X – axis at (-3, 0) and (4, 0).
So, the zeroes of the polynomial are -3 and 4.
Justification:
Given p(x) = x2 – x – 12 = 0
⇒ x2 – 4x + 3x – 12 = 0
⇒ x(x – 4) + 3(x – 4) = 0
⇒ (x – 4) (x + 3) = 0
⇒ x – 4 = 0 and x + 3 = 0
x = 4 and x = – 3
ii) Given polynomial p(x) = x2 – 6x + 9
List of values of p(x):
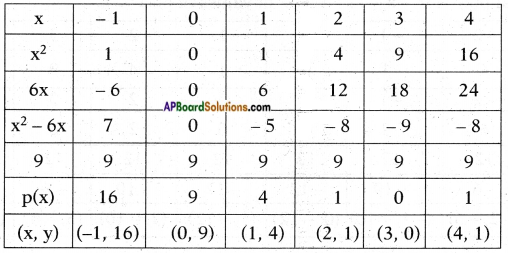
Now, let’s locate the points listed above on a graph paper and draw the graph.
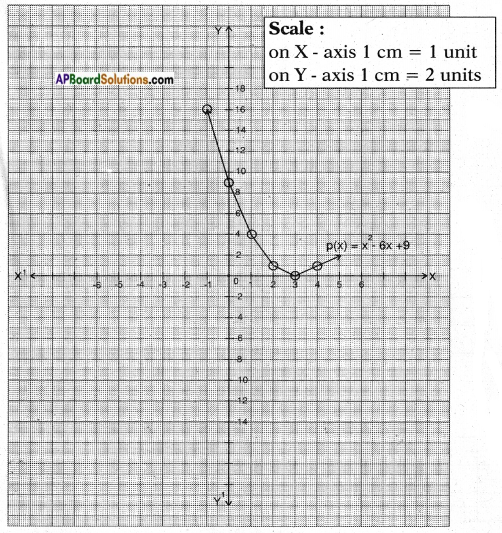
Result: We observe that the graph cuts the X – axis at (3, 0).
So, the zeroes of the given polynomial are same i.e., 3.
Justification:
Given p(x) = x2 – 6x + 9
⇒ x2 – 3x – 3x + 9 = 0
⇒ x(x – 3) – 3(x – 3) = 0
⇒ (x – 3) (x – 3) = 0
⇒ x – 3 = 0 and x – 3 = 0
x = 3 and x = 3
![]()
iii) Given polynomial p(x) = x2 – 4x + 5
List of values of p(x):
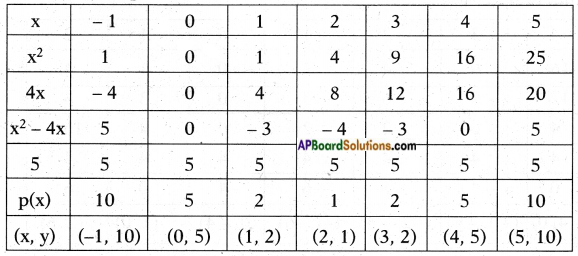
Now, let’s locate the points listed above on a graph paper and draw the graph.
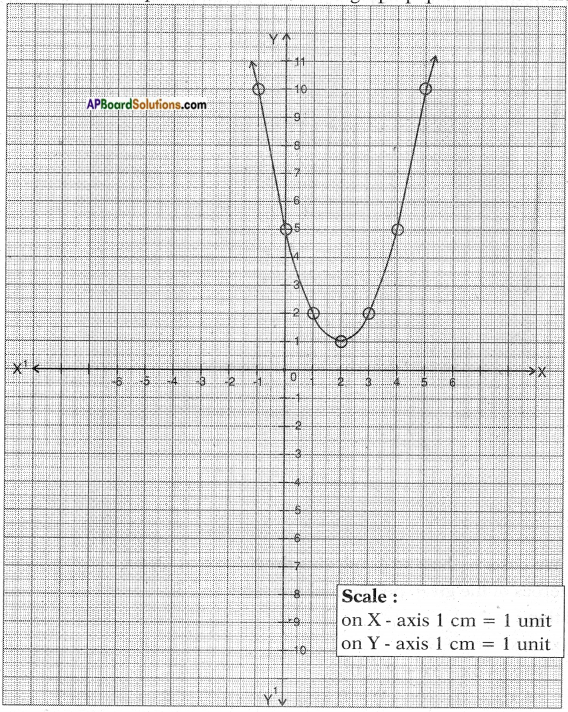
Result: We observe that the graph does not cut the X – axis at any point.
So, the quadratic polynomial p(x) has no zeroes.
Justification: For the given p(x) = x2 – 4x + 5 not possible to split in factors.
iv) Given polynomial p(x) = x2 + 3x – 4.
List of values of p(x):
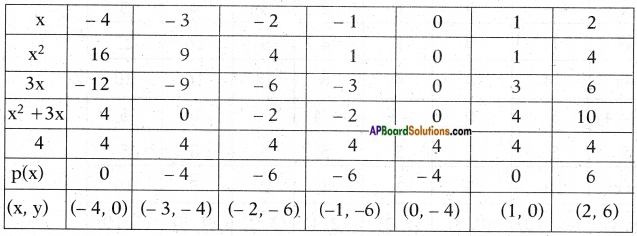
Now, let’s locate the points listed above on a graph paper and draw the graph.
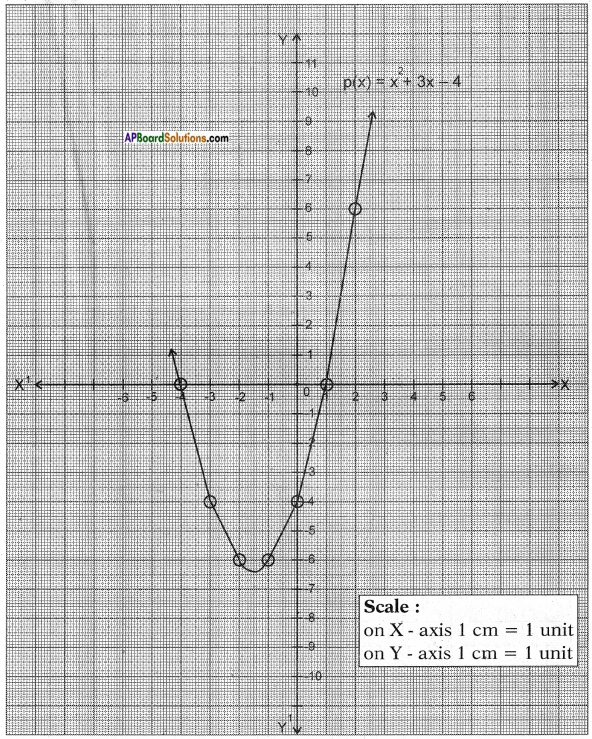
Result: We observe that the graph cuts the X – axis at (-4, 0) and (1, 0).
So, the zeroes of the polynomial are -4 and 1.
Justification:
Given p(x) = x2 + 3x – 4 = 0
⇒ x2 + 4x – x – 4 = 0
⇒ x(x + 4)- 1(x + 4) = 0
⇒ (x + 4) (x – 1) = 0
⇒ x + 4 = 0 and x – 1 = 0
x = – 4 and x = 1
![]()
v) Given polynomial p(x) = x2 – 1
List of values of p(x):
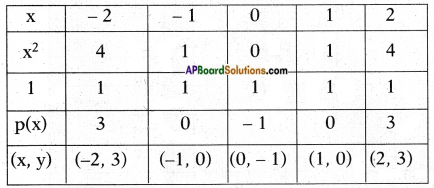
Now, let’s locate the points listed above on a graph paper and draw the graph.
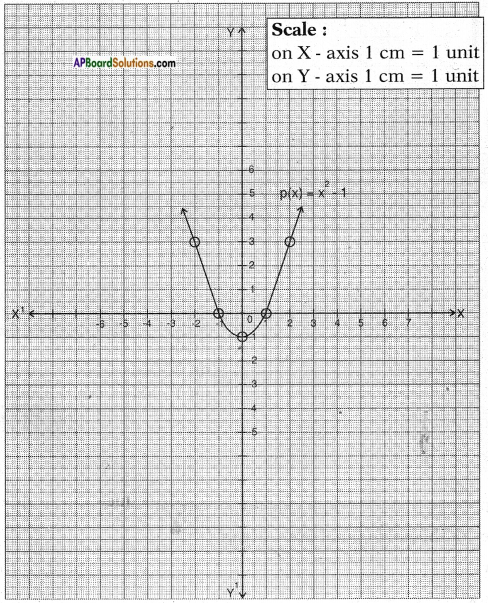
Result: We observe that the graph cuts the X – axis at (-1, 0) and (1,0).
So, the zeroes of the polynomial are – 1 and 1.
Justification:
Given p(x) = x2 – 1 = 0
⇒ p(x) = (x + 1) (x – 1) = 0 [∵ a2 – b2 = (a + b) (a – b)]
⇒ x + 1 = 0 and x – 1 = 0
x = -1 and x = 1
Question 4.
Why are \(\frac{1}{4}\) and -1 zeroes of the polynomial p(x) = 4x2 + 3x – 1 ?
Answer:
Given polynomial p(x) = 4x2 + 3x – 1
Given zeroes are \(\frac{1}{4}\) and -1
Let x = \(\frac{1}{4}\)

Let x = -1
⇒ p(-1) = 4(-1)2 + 3(-1)-1 = 4 – 3 – 1 = 4 – 4 = 0
∴ P(\(\frac{1}{4}\)) = 0 and p(-1) = 0
So these values are zeroes of the polynomial p(x).
