AP SSC 10th Class Maths Solutions Chapter 10 Mensuration Ex 10.3

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 10 Mensuration Ex 10.3 Textbook Questions and Answers.

AP State Syllabus SSC 10th Class Maths Solutions 10th Lesson Mensuration Exercise 10.3

10th Class Maths 10th Lesson Mensuration Ex 10.3 Textbook Questions and Answers

Question 1.
An iron pillar consists of a Cylindrical portion of 2.8 m. height and 20 cm. in diameter and a cone of 42 cm. height surmounting it. Find the weight of the pillar if 1 cm³ of iron weighs 7.5 g.
Answer:
Volume of the iron pillar = Volume of the cylinder + Volume of the cone
Cylinder:

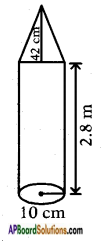
Radius = \(\frac{d}{2}\) = \(\frac{20}{2}\) = 10 cm
Height = 2.8 m = 280 cm
Volume = πr²h
= \(\frac{22}{7}\) × 10 × 10 × 280
= 88000 cm³
Cone:
Radius ‘r’ = \(\frac{d}{2}\) = \(\frac{20}{2}\) = 10 cm
height ‘h’ = 42 cm
Volume = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 10 × 10 × 42
= 4400 cm³
∴ Total volume = 88000 + 4400 = 92400 cm³
∴ Total weight of the pillar at a weight of 7.5 g per 1 cm³ = 92400 × 7.5
= 693000 gms
= \(\frac{693000}{1000}\) kg
= 693 kg.

Question 2.
A toy is made in the form of hemisphere surmounted by a right cone whose circular base is joined with the plane surface of the hemisphere. The radius of the base of the cone is 7 cm. and its volume is 3/2 of the hemisphere. Calculate the height of the cone and the surface area of the toy correct to 2 places of decimal.
(Take π = \(3 \frac{1}{7}\))
Answer:

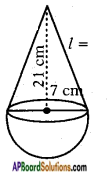
Given r = 7 cm and
Volume of the cone = \(\frac{3}{2}\) volume of the hemisphere
\(\frac{1}{3}\)πr²h = \(\frac{3}{2}\) × \(\frac{2}{3}\) × πr³
∴ h = 3r
= 3 × 7 = 21 cm
Surface area of the toy = C.S.A. of the cone + C.S.A. of hemisphere
Cone:
Radius (r) = 7 cm
Height (h) = 21 cm
Slant height l = \(\sqrt{r^{2}+h^{2}}\)
= \(\sqrt{7^{2}+21^{2}}\)
= \(\sqrt{49+441}\)
= √490
= 22.135 cm.
∴ C.S.A. = πrl
= \(\frac{22}{7}\) × 7 × 22.135 = 486.990 cm²
Hemisphere:
Radius (r) = 7 cm
C.S.A. = 2πr²
= 2 × \(\frac{22}{7}\) × 7 × 7
= 308 cm²
C.S.A. of the toy = 486.990 + 308 = 794.990 cm²

Question 3.
Find the volume of the largest right circular cone that can be cut out of a cube whose edge is 7 cm.
Answer:
Radius of the cone with the largest volume that can be cut out from a cube of edge 7 cm = \(\frac{7}{2}\) cm

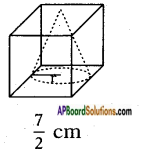
Height of the cone = edge of the cube = 7 cm
∴ Volume of the cone V = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) × 7
= 89.83 cm³.

Question 4.
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of right circular cone mounted on a hemisphere is immersed into the tub. The radius of the hemi¬sphere is 3.5 cm and height of cone outside the hemisphere is 5 cm. Find the volume of water left in the tub. (Take π = \(\frac{22}{7}\))
Answer:

The tub is in the shape of a cylinder, thus
Radius of the cylinder (r) = 5 cm
Length of the cylinder (h) = 9.8 cm
Volume of the cylinder (V) = πr²h
= \(\frac{22}{7}\) × 5 × 5 × 9.8
Volume of the tub = 770 cm³.
Radius of the hemisphere (r) = 3.5 cm
Volume of the hemisphere = \(\frac{2}{3}\)πr³
= \(\frac{2}{3}\) × \(\frac{22}{7}\) × 3.5 × 3.5 × 3.5
= \(\frac{22 \times 12.25}{3}\)
= \(\frac{269.5}{3}\)
Radius of the cone (r) = 3.5 cm
Height of the Cone (h) = 5 cm
Volume of the cone V = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 3.5 × 3.5 × 5
= \(\frac{192.5}{3}\)
Volume of the solid = Volume of the hemisphere + Volume of the cone
= \(\frac{269.5}{3}\) + \(\frac{192.5}{3}\) = \(\frac{462}{3}\) = 154 cm³
Now, when the solid is immersed in the tub, it replaces the water whose volume is equal to volume of the solid itself.
Thus the volume of the water replaced = 154 cm³.
∴ Volume of the water left in the tub = Volume of the tub – Volume of the solid = 770 – 154 = 616 cm³.

Question 5.
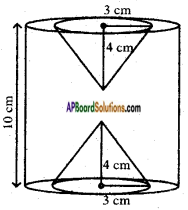
In the adjacent figure, the height of a solid cylinder is 10 cm and diameter 7 cm. Two equal conical holes of radius 3 cm and height 4 cm are cut off as shown in the figure. Find the volume of the remaining solid.

Answer:
Volume of the remaining solid = Volume of the given solid – Total volume of the two conical holes
Radius of the given cylinder (r) = \(\frac{d}{2}\) = \(\frac{7}{2}\) = 3.5 cm
Height of the cylinder (h) = 10 cm
Volume of the cylinder (V) = πr²h
= \(\frac{22}{7}\) × 3.5 × 3.5 × 10
= \(\frac{2695}{7}\)
= 385 cm³.
Radius of each conical hole, ‘r’ = 3 cm
Height of the conical hole, h = 4 cm
Volume of each conical hole,
V = \(\frac{1}{3}\)πr²h = \(\frac{1}{3}\) × \(\frac{22}{7}\) × 3 × 3 × 4
= \(\frac{792}{21}\)
= \(\frac{264}{7}\)
Total volume of two conical holes = 2 × \(\frac{264}{7}\) = \(\frac{528}{7}\) cm³
Hence, the remaining volume of the solid

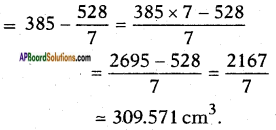
Question 6.
Spherical marbles of diameter 1.4 cm. are dropped into a cylindrical beaker of diameter 7 cm., which contains some water. Find the number of marbles that should be dropped into the beaker, so that water level rises by 5.6 cm.
Answer:
Rise in the water level is seen in cylindrical shape of Radius = Beaker radius
= \(\frac{d}{2}\) = \(\frac{7}{2}\) = 3.5 cm

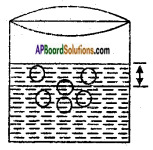
Height ‘h’ of the rise = 5.6 cm.
∴ Volume of the ‘water rise’ = πr²h
= \(\frac{22}{7}\) × 3.5 × 3.5 × 5.6
= \(\frac{22 \times 12.25 \times 5.6}{7}\)
= 215.6
Volume of each marble dropped = \(\frac{4}{3}\)πr³
Where radius r = \(\frac{d}{2}\) = \(\frac{1.4}{2}\) = 0.7 cm
∴ V = \(\frac{4}{3}\) × \(\frac{22}{7}\) × 0.7 × 0.7 × 0.7
= 1.4373 cm³
∴ Volume of the ‘rise’ = Total volume of the marbles.
Let the number of marbles be ‘n’ then n × volume of each marble = volume of the rise.
n × 1.4373 = 215.6
= \(\frac{215.6}{1.4373}\)
∴ Number of marbles = 150.

Question 7.
A pen stand is made of wood in the shape of cuboid with three conical depressions to hold the pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depression is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand.

Answer:
Volume of the wood in the pen stand = Volume of cuboid – Total volume of three depressions.
Length of the cuboid (l) = 15 cm
Breadth of the cuboid (b) = 10 cm
Height of the cuboid (h) = 3.5 cm
Volume of the cuboid (V) = lbh = 15 × 10 × 3.5 = 525 cm³.
Radius of each depression (r) = 0.5 cm
Height / depth (h) = 1.4 cm
Volume of each depressions V = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 0.5 × 0.5 × 1.4
= \(\frac{7.7}{3 \times 7}\) = \(\frac{1.1}{3}\) cm³
Total volume of the three depressions = 3 × \(\frac{1.1}{3}\)
= 1.1 cm³
∴ Volume of the wood = 525 – 1.1 = 523.9 cm³