Andhra Pradesh BIEAP AP Inter 2nd Year Chemistry Study Material 1st Lesson Solid State Textbook Questions and Answers.
AP Inter 2nd Year Chemistry Study Material 1st Lesson Solid State
Very Short Answer Questions
Question 1.
Define the term amorphous.
Answer:
An amorphous (no form) solid is the compound which does not have orderly arrangement of particles. In amorphous solids the constituent particles, atoms, molecules has short range order only.
E.g.: Glass, rubber, plastics etc.,
![]()
Question 2.
What makes a glass different from quartz ?
Answer:
- Glass is an amorphous solid in which the constituent particles have only a short range order.
- Quartz is a crystalline form of silica in which constituent particles have long range order.
Question 3.
Classify the following solids as ionic, metallic, molecular, covalent network or amorphous.
i) Si
ii) I2
iii) P4
iv) Rb
v) SiC
vi) LiBr
vii) Ammonium .Phosphate (NH4)3 PO4
viii) Plastic
ix) graphite
x) Tetra phosphorous decoxide
xi) brass
Answer:
i) Si – Covalent network solid
ii) I2 – Molecular solid with covalent bonds
iii) P4 – Molecular solid with covalent bonds ,
iv) Rb – Metallic solid
v) SiC – Giant molecular Network Solid with covalent bonds
vi) LiBr – Ionic solids
vii) Ammonium Phsophate (NH4)3 PO4 – Ionic Solids
viii) Plastic – Amorphous solid
ix) Graphite – Hexagonal network solid with covalent bonds (giant molecule)
x) Tetra phosphorous decoxide (P4O6) – Molecular solid with covalent bonds.
xi) Brass – Metallic solid
Question 4.
What is meant by the term coordination number ?
Answer:
The number of nearest neighbouring particles of a particle is defined as the co-ordination number.
(Or)
The number of nearest oppositely charged ions surrounding a particular ion is also called as co-ordination number.
E.g.: Co-ordination no. of Na+ in NaCl lattice is ‘6’.
Question 5.
What is the co-ordination number of atoms in a cubic close – pack structure ?
Answer:
The co-ordination number of atoms in a cubic close pack structure is ’12’.
![]()
Question 6.
What is the co-ordination number of atoms in a body – centered cubic structure ?
Answer:
The co-ordination number of atoms in a body – centered cubic structure is ‘8’.
Question 7.
Stability of a crystal is reflected in the magnitude of its melting point. Comment.
Answer:
Stability of a crystal is reflected in the magnitude of its melting point.
Explanation :
- The stability of a crystal mainly depends upon the magnitude of forces of attraction between the constituent particles.
- As the attractive forces between the constituent particles increases stability of the crystal aslo increases.
- As the stability of crystal increases melting point of solid will be higher.
Question 8.
How are the intermolecular forces amonj the molecules affect the melting point ?
Answer:
- As the intermolecular forces between constituent particles of solid increases, stability of the compound increases.
- As the stability of crystal increases belting point of solid also increases (high).
Question 9.
How do you distinguish between hexagonal close – packing and cubic close – packing structures ?
Answer:
Hexagonal close packing : The spheres of the 3rd layer are exactly aligned with those of first layer. This pattern of spheres is repeated in alternate layers. Tetrahedral voids of the 2nd layer may be covered by the spheres of 3rd layer. This structure is called hexagonal close packed (hep) structure.
Cubic close packing : The spheres of 3rd layer cover the octahedral voids of 2nd layer. But the spheres of 4th layers are aligned with those of first layer. This structure is called cubic close packing.
![]()
Question 10.
How do you distinguish between crystal lattice and unit cell ?
Answer:
Crystal lattice : A regular arrangement of the constituent particles of a crystal in the three dimensional space is called crystal lattice.
Unit cell: The simple unit of crystal lattice which when repeated again and again gives the entire crystal of a given substance is called unit cell.
Question 11.
How many lattice points are there in one unit cell of face centered cubic lattice ?
Answer:
In face centered cubic unit cell.
The number of comer atoms per unit cell.
= 8 comer atoms × \(\frac{1}{8}\) atom per unit cell = 8 × \(\frac{1}{8}\) =1 atom
Number of face centered atoms per unit cell
= 6 face centered atoms × \(\frac{1}{2}\) atom per unit cell
= 6 × \(\frac{1}{8}\) = 3 atoms
∴ Total no. of lattice points = 1 + 3 = 4.
Question 12.
How many lattice points are there in one unit cell of face – centered tetragonal lattice ?
Answer:
In face centered tetragonal unit cell
Number of face centered atoms per unit cell
= 6 face centered atoms × \(\frac{1}{2}\) atom per unit cell
= 6 × \(\frac{1}{2}\) = 3 atoms
∴ Total no. of lattice points = 1 + 3 = 4.
![]()
Question 13.
How many lattice points are there in one unit cell of body centered cubic lattice ?
Answer:
In body – centered cubic unit cell
The number of comer atoms per unit cell
= 8 comers × \(\frac{1}{8}\) per comer atom
= 8 × \(\frac{1}{8}\) = 1 atom
Number of atoms at body center = 1 × 1 = 1 atom
∴ Total no. of lattice points = 1 + 1 = 2.
Question 14.
What is a semi conductor ?
Answer:
The solids which are having moderate conductivity between insulators and conductors are called semi conductors.
These have the conductivity range from 10-6 to 104 Ohm-1 m-1.
By doping process the conductivity of semi conductors increases.
E.g. : Si, Ge crystal.
Question 15.
What is Schottky defect ?
Answer:
Schottky defect:
- It is a point defect in which an atom or ion is missing from its normal site in the lattice”.
- In order to maintain electrical neutrality, the number of missing cations and anions are equal.
- This sort of defect occurs mainly in highly ionic compounds, where cationic and anionic sizes are similar.
In such compounds the co-ordination number in high.
Ex.: NaCl, CsCl etc. - Illustration:
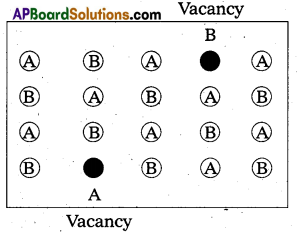
- This defect decreases the density of the substance.
Question 16.
What is Frenkel defect ?
Answer:
Frenkel defect:
- “It is a point defect in which an atom or ion is shifted from its normal lattice position”. The ion or the atom now occupies an interstitial position in the lattice.
- This type of a defect is favoured by a large difference in sizes between the cation and anion. In these compounds co-ordination number is low.
E.g.: Ag – halides, ZnS etc. - Illustration:
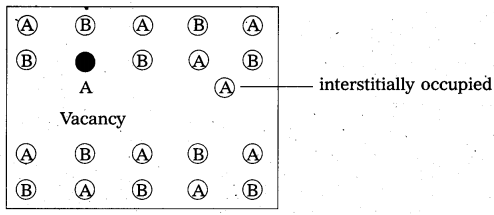
- Frenkel defect do not change the density of the solids significantly.
![]()
Question 17.
What is interstitial defect ?
Answer:
- Some of the constituent particles of solid compound occupy an interstitial site, the crystal is said to have interstitial defect.
- This defect shown by ionic solid, non-ionic solids which are maintaining electrical neutrality.
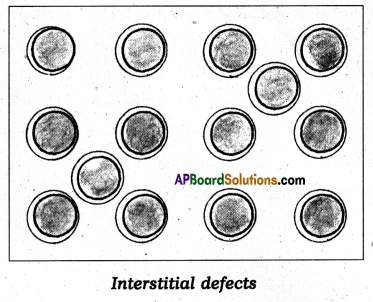
Question 18.
What are f – centers ?
Answer:
- f – centers are the anionic sites occupied by unpaired electrons.
- These impart colour to cyrstals. This colour is due to the excitation of electrons when they absorb energy from the visible light.
- f – centres are formed by heating alkyl halide with excess of alkali metal.
E.g.: NaCl crystals heated in presence of Na – vapour yellow colour is produced due to f – centres.
Question 19.
Explain Ferromagnetism with suitable example.
Answer:
Ferromagnetic Substances : Some substances containing more number of unpaired electrons are very strongly attracted by the external magrietic field. In Ferromagnetic substances the Magnetic moments in individual atoms are all alligned in the same direction. Such substances are called Ferromagnetic Substances. In ferromagnetic substances the field strength B > > > H.
E.g. : Fe, Co and Ni.
![]()
Question 20.
Explain paramagnetism with suitable example.
Answer:
Paramagnetic Substances : If the magnetic lines of forces are drawn into the substance the field (B) in the substances is greater than the applied field (H) i.e., B > H. Such a substance is called paramagnetic substance. Paramagnetic substance moves from a weaker part of the field to a stronger part of the field. Paramagnetic substances are weakly attracted in a external Magnetic field. They exhibit paramagnetism due to the presence of unpaired electrons.
E.g. : Cr+3, Sc+2, K3 [Fe (CN)6].
Question 21.
Explain Ferrimagnetisms with suitable example.
Answer:
Ferrimagnetism is observed when the magnetic moments of the domains in the substance are aligned in parallel and anti parallel directions in unequal numbers.
- These are weakly attracted by magnetic field as compared to ferromagnetic substances.
- These lose ferrimagnetism on heating and becomes paramagnetic.
Question 22.
Explain Antiferromagnetism with suitable example.
Answer:
Substances like Mno showing anti-ferromagnetism having domain structure similar to ferromagnetic substance, but their domains are oppositely oriented and cancel out each others magnetic moment.
Question 23.
Why X – rays are needed to probe the crystal structure ?
Answer:
According to the principles of optics, the wavelength of light used to observe an object must be no greater than the twice the length of the object it self. It is impossible to see atom s using even the finest optical microscope. To see the atoms we must use light with a wavelength of approximately 10-10 m. X – rays are present with in this region of electromagnetic spectrum. So X – rays are used to probe crystal structure.
Short Answer Questions
Question 1.
Explain similarities and differences between metallic and ionic crystals.
Ans:
Similarities between ionic and metallic crystals :
- Both ionic and metallic crystals have electrostatic force of attraction.
- The bond present in ionic crystals and metallic crystals is non-directional.
Differences between ionic and metallic crystals :
Ionic Crystals
- In ionic crystals electrostatic force is in between oppositely charged ions.
- These are good conductors of electricity.
- Ionic bond in ionic crystals is strong.
Metallic Crystals
- In metallic crystals electrostatic force is in between the valency electrons.
- These are goods conductors of electricity in solid state.
- Metallic bond in metallic crystals is weak (or) strong.
![]()
Question 2.
Explain why ionic solids are hard and brittle.
Answer:
In ionic solids the formation of solid compound is due to the arrangements of cations and anions bound by strong coloumbic force i.e., electro static force. So ionic solids are hard and brittle in nature. These have high melting and boiling points.
Question 3.
Calculate the efficiency of packing in case of a metal of simple cubic crystal.
Answer:
Packing efficiency in case of metal of simple cubic crystal:
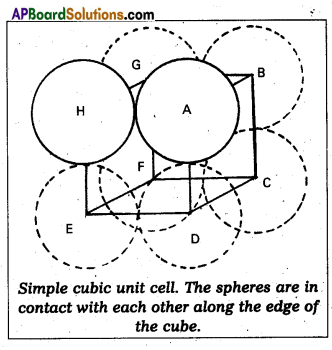
The edge length of the cube
a = 2r. (r = radius of particle)
Volume of the cubic unit cell = a3 = (2r)3
= 8r3
∵ A simple cubic unit cell contains only one atom
The volume of space occupied = \(\frac{4}{3}\) πr3
∴ Packing efficiency
= \(\frac{\text { Volume of one atom }}{\text { Volume of cubic unit cell }}\) × 100
= \(\frac{4 / 3 \pi r^{3}}{8 r^{3}}\) × 100 = \(\frac{\pi}{6}\) × 100 = 52.36%.
Question 4.
Calculate the efficiency of packing in case of a metal of body centered cubic crystal.
Answer:
Packing efficiency in case of a metal of body centred cubic crystal:
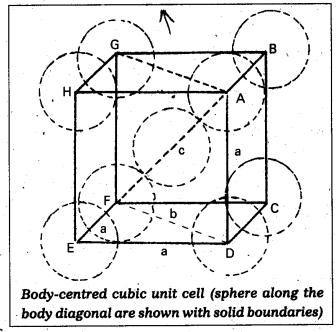
in B.C.C. Crystal
\(\sqrt{3}\)a = 4r
a = \(\frac{4 \mathrm{r}}{\sqrt{3}}\)
In this structure total no. of atoms is ‘2’ and their volume = 2 × (\(\frac{4}{3}\)) πr3
Volume of the cube = a3 = (\(\frac{4}{\sqrt{3}}\)r)3
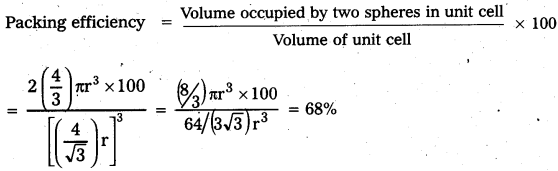
![]()
Question 5.
Calculate the efficiency of the packing incase of face – centered cubic crystal.
Answer:
Packing efficiency of face centered cubic crystal:
In fcc lattice assume that atoms are touching each other. Here unit cell edge length
a = 2\(\sqrt{2}\) r
Each unit cell as effectively four spheres.
Total volume of four spheres = 4 × (\(\frac{4}{3}\)) πr3
Volume of cube = a3 = (2\(\sqrt{2}\)r)3

Question 6.
A cubic solid is made of two elements P and Q. Atoms of Q are at the corners of the cube and P at the body – centre. What is the formula of the compound ? What are the coordination numbers of P and Q?
Answer:
The contribution of atoms Q present at 8 corners of the cube = \(\frac{1}{8}\) × 8 = 1
The contribution of atoms P present at the body centre = 1
Therefore ratio of P and Q = 1 : 1
So, the formula of the compound is PQ.
Co-ordination number of atoms P and Q = 8.
Question 7.
If the radius of the octahedral void is ‘r and radius of the atoms in close packing is ‘R’, derive relation between r and R.
Answer:
Derivation of relation between r and R:
Octahedral void is shown in the following diagram as a shaded circle.
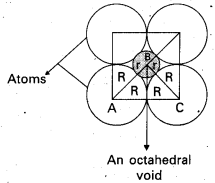
∴ ∆ ABC is a right angled triangle.
∴ We apply pythagoras theorem.
AC2 = AB2 + BC2
(2R)2 = (R + r)2 + (R + r)2 = 2 (R + r)2
4R2 = 2 (R + r)2
2R2 = (R + r)2
(\(\sqrt{2}\) R)P = (R + r)2
\(\sqrt{2}\) R = R + r
r = \(\sqrt{2}\) R – R
r = (\(\sqrt{2}\) – 1)R
r = (1.414- 1) R
r = 0.414 R.
![]()
Question 8.
Describe the two main types of semiconductors and contrast their conduction mechanism. [A.P. Mar. 19]
Answer:
The solids which are having moderate conductivity between insulators and conductors are called semi conductors.
These have the conductivity range from 10-6 to 104 Ohm-1m-1.
By doping process the conductivity of semi conductors increases. E.g.: Si, Ge, crystal.
Semi conductors are Of two types. They are :
1. Intrinsic semi-conductors : In case of semi-conductors, the gap between the valence band and conduction band is small. Therefore, some electrons may jump to conduction band and show some conductivity. Electrical conductivity of semi-conductors increases with rise in “temperature”, since more electrons can jump to the conduction band. Substances like silicon and germanium show this type of behaviour and are called intrinsic semi-conductors.
2. Extrinsic semi – conductors : Their conductivity is due to the presence of impurities.
They are formed by “doping”. ,
Doping: Conductivity of semi-conductors is too low to be of pratical use. Their conductivity is increased by adding an appropriate amount of suitable impurity. This process is called “doping”.
Doping can be done with an impurity which is electron rich or electron deficient.
Extrinsic semi-conductors are of two types.
a) n-type semi-conductors : It is obtained by adding trace amount of V group element (P, As, Sb) to pure Si or Ge by doping.
When P, As, Sb (Or) Bi is added to Si or Ge some of the Si or Ge in the crystal are replaced by P or As atoms and four out of five electrons of P or As atom will be used for bonding with Si or Ge atoms while the fifth electron serve to conduct electricity.
b) p-type semi-conductors : It is obtained by doping with impurity atoms containing less electrons i.e., III group elements (B, Al, Ga or In).
When B or Al is added to pure Si or Ge some of the Si or Ge in the crystal are replaced by B or AZ atoms and four out of three electrons of B or Al atom will be used for bonding with “Si” or Ge atoms while the fourth valence electron is missing is called electron hole (or) electron vacancy. This vacancy on an atom in the structure migrates from one atom to another. Hence it facilitates the electrical conductivity.
Question 9.
Classify each of the following as either a p – type or a n – type semiconductor.
1. Ge doped with In
2. Si doped with B.
Answer:
Both (1) and (2) come under “p – type semiconductors”.
Reason: In both the cases dopants (i.e.,) Indium in case – (1) and Boron in case – (2) belong to III (or) 13th group. Si (or) Ge doped with III group element is known as p-type semi- conductor.
Explanation : Doping the silicon or germanium element with III or 13th group element like “B”, Al, Ga or “In” results in the substitution of some silicon atoms in its structure by the dopant. The dopant has only three valency electrons. The fourth valency electron is required. It is left as a vacant place on the atom. It is known as an ‘electron vacancy’ (or) a ‘hole’. The electron vacancy on ah atom in the structure migrates from one atom to another. Hence it facilitates the electrical conductivity. Si (or) Ge, doped with elements that create a hole in the structure, is known as p- type semi-conductor.
![]()
Question 10.
Analysis shows that nickel oxide has the formula Ni0.980, 1.00, what fractions of nickel exist as Ni2+ and Ni3+ ions ?
Answer:
In pure nickel oxide (NiO) the ratio of Ni and O atoms = 1 : 1
Let x be the no. of Ni (II) atoms replaced by Ni (III) atoms in the oxide
∴ Number of Ni (II) atoms present = 0.98 – x
Total charge on Ni atoms = charge on oxygen atom (∵ the oxide is neutral)
2 (0.98 – x) + 3x = 2
1.96 – 2x + 3x = 2
x = 2 – 1.96 = 0.04
No. of Ni (iii) atoms
% of Ni (III) atoms in Nickel oxide = ![]() × 100
× 100
= \(\frac{0.04}{0.98}\) × 4.01%
% of Ni (II) atoms in nickel oxide = 100 – 4.01 = 95.99%
Question 11.
Gold (atomic radius = 0.144 nm) crystallizes in a face centered unit cell. What is the length of a side of the unit cell ?
Answer:
In a fee unit cell .
The edge length a = 2\(\sqrt{2}\) r
Given r = 0.144 nm
= 2 × 1.414 × 0.144 = 0.407 nm.
Question 12.
In terms of band theory, what is the difference between a conductor and an insulator ?
Answer:
In case of metals (conductors) the atomic orbitals forms molecular orbitals which are close in energy to each other as to form a band called valency band. If this band is partially filled (or) it overlaps with a higher energy unoccupied band called conduction band. Then electrons can flow easily under an applied electric field and the metal shows conductivity.
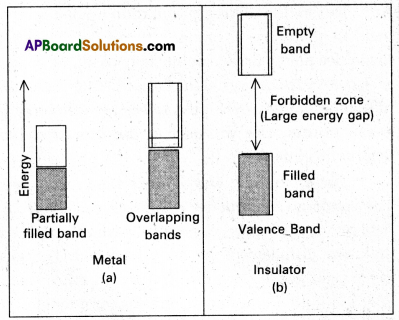
In case of insulators the gap between filled valence band and the next higher un occupied band is large, electrons cannot jump to it and such a substance has very small conductivity.
![]()
Question 13.
In terms of band theory, what is the difference between a conductor and a semiconductor?
Answer:
In case of metals (conductors) the atomic orbitals forms molecular orbitals which are close in energy to each other as to form a band called valency band. If this band is partially filled (or) it overlaps with a higher energy unoccupied band called conduction band. Then electrons can flow easily under an applied electric field and the metal shows conductivity.
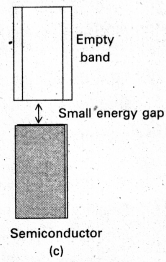
In case of semi conductors, the gap between the valence band and conduction band is small. So some of electrons may jump to conduction band and show some conductivity.
Question 14.
If NaCl is doped with 1 × 10-3 mol percent of SrCl2, what is the concentration of cation vacancies ?
Answer:
The addition of SrCl2 to NaCl , each Sr+2 ion replaces two Na+ ions and occupies only one lattice point in place of Na+. Due to this one cation vacancy arised.
The number of moles of cation vacancies in 100 moles of NaCl = 1 × 10-3
The number of moles of cation vacancies in 1 moles NaCl = \(\frac{1 \times 10^{-3}}{100}\) = 10-5 mole
Total number of cation vacancies = 10-5 × 6.023 × 1023 = 6.023 × 1018.
Question 15.
Derive Bragg’s equation. [T.S. Mar. 19, 16, 15; A.P. Mar. 17, 16, 15] [Mar. 14]
Answer:
Derivation of Bragg’s equation : When X-rays are incident on the crystal or plane, they are diffracted from the lattice points (lattice points may be atoms or ions or molecules). In the crystal the lattice points are arranged in regular pattern. When the waves are diffracted from these points, the waves may be constructive or destructive interference.
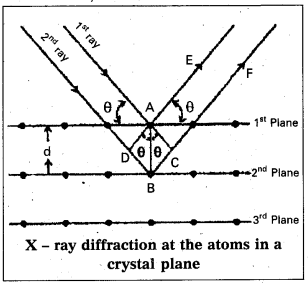
The 1st and 2nd waves reach the crystal surface. They undergo constructive interference. Then from the figure 1st and 2nd rays are parallel waves. So, they travel the same distance till the wave form AD. The second crystal plane
ray travels more than the first by an extra distance (DB + BC) after crossing the grating for it to interfere with the first ray in a constructive manner. Then only they can be in the same phase with one another. If the two waves are to be in phase, the path difference between the two ways must be equal to the wavelength Q.) or integral multiple of it (nλ, where n = 1, 2, 3 )
(i.e.,) nλ = (DB + BC) [where n = order of diffraction]
DB = BC = d sin θ [θ = angle of incident beam,]
(DB + BC) = 2d sin θ [d = distance between the planes]
nλ = 2d sin θ
This relation is known as Bragg’s equation.
Long Answer Questions
Question 1.
How do you determine the atomic mass of an unknown metal If you know Its density and dimension of its unit cell? Explain.
Answer:
Let the, Atomic weight of crystalline substance = M
Avogadros number = N0
No. of atoms present per unit cell = Z
Density of unit cell or of the substance = ρ
Unit cell length = a
So, volume of the unit cell = a3 (= V)
∴ Then, mass corresponding to each lattice point = M/N0
∴ Mass of ‘Z lattice points = \(\frac{\mathrm{ZM}}{\mathrm{N}_{0}}\)
∴ Density (p) of unit cell = \(\frac{\text { mass }}{\text { volume }}=\frac{\frac{\mathrm{Z} \cdot \mathrm{M}}{\mathrm{N}_{0}}}{\mathrm{a}^{3}}=\frac{\mathrm{ZM}}{\mathrm{N}_{0} \mathrm{a}^{3}}\)
Atomic weight M = \(\frac{\rho \times \mathrm{a}^{3} \mathrm{~N}_{0}}{\mathrm{Z}}\)
![]()
Question 2.
Silver crystallizes in FCC lattice. If edge of the cell is 4.07 × 10-8 and density is 10.5 g. cm-3. Calculate the atomic mass of silver.
Answer:
Given data
d = 10.5 g/cm3
a = 4.07 × 10-8 cm
Z = 4 atoms
NA = 6.023 × 1023
Formula M = \(\frac{\mathrm{d} \times \mathrm{a}^{3} \times \mathrm{N}_{\mathrm{A}}}{\mathrm{Z}}\)
= \(\frac{10.5 \times\left(4.07 \times 10^{-8}\right)^{3} \times 6.023 \times 10^{23}}{4}\)
= \(\frac{10.5 \cdot \times 67.767 \times 10^{-24} \times 6.023 \times 10^{23}}{4}\)
= 107.09 gm/mole.
Question 3.
Niobium crystallizes in body – centered cubic structure. If density is 8.55 g cm-3, calculate atomic radius of niobium using its atomic mass 93 U.
Answer:
Radius of unit cell in bcc structure = \(\frac{\sqrt{3}}{4}\) a
First we have to calculate edge length of unit cell ‘a’
Given Atomic mass of Niobium = 93 g/mole
No. of particles in bcc type unit cell (Z) = 2
mass of unit cell = \(\frac{\mathrm{ZM}}{\mathrm{N}_{\mathrm{A}}}=\frac{2 \times 93}{6.023 \times 10^{23}}\) = 30.89 × 1023 gms
Given Density (d) = 8.55 gm/cm3
Volume of unit cell (a3) = \(\frac{\text { mass }}{\text { density }}=\frac{30.89 \times 10^{23}}{8.55}\)
= 36.16 × 10-24 cm3.
Edge length of unit cell (a) = (36.13 × 10-24)1/3
= 3.31 × 10-8 cm
radius of Unit cell (r) = \(\frac{\sqrt{3}}{4}\) a
= \(\frac{\sqrt{3} \times 3.31 \times 10^{-8}}{4}\)
= 1.43 × 10-8 cm = 143 pm.
Question 4.
Copper crystallizes into a FCC lattice with edge length 3.61 × 10-8 cm. Show that the calculated density is in agreement with its measured value of 8.92 g.cm-3.
Answer:
Density d = \(\frac{\mathrm{ZM}}{\mathrm{a}^{3} \times \mathrm{N}_{\mathrm{A}}}\)
Given edge length 3.61 × 10-8 cm
For FCC lattice of copper, Z = 4
Atomic mass of copper M = 63.5 gms/mole
d = \(\frac{4 \times 63.5}{\left(3.61 \times 10^{-8}\right)^{3} \times 6.023 \times 10^{23}}\)
= 8.97 g/cm3
The calculated value is approximately in agreement with the measured value 8.92 g/cm3.
![]()
Question 5.
Ferric oxide crystallizes in a hexagonal close – packed array of oxide ions with two of every three octahedral holes occupied by ferric ions. Derive the formula of ferric oxide.
Answer:
Given ferric oxide crystallises in a hexagonal close packed array of oxide ions with two out of every three octahedral,holes occupied by ferric ions.
In hexagonal close – packed arrangement there is one octahedral hole for each atom. If the number of oxide ions (O-2) per unit cell is one, then the number of Fe+3 ions = 2/ 3 × octahedral holes.
= 2/3 × 1 = 2/3
The formula of the compound = Fe2/3 O1 (or) Fe2 O3.
Question 6.
Aluminium crystallizes in a cubic close packed structure. Its metallic radius is 125 pm.
i) What is the length of the side of the unit cell.
ii) how many unit cells are there in 1.00 cm3 of aluminium.
Answer:
i) Given radius = 125 pm
For a fcc lattice unit cell r = \(\frac{a}{2 \sqrt{2}}\)
a = 2\(\sqrt{2}\) × r
= 2 × 1.414 × 125 = 353.5 pm
∴ Length of the side of the unit cell = 353.5 pm
ii) Volume of unit cell = a3 = (353.5 × 10-10 cm)3
= 442 × 10-25 cm3
Number of unit cell = \(\frac{1}{4.42 \times 10^{-25}}\)
= 2.26 × 1022 unit cells.
Question 7.
How do you obtain the diffraction pattern for a crystalline substance ?
Answer:
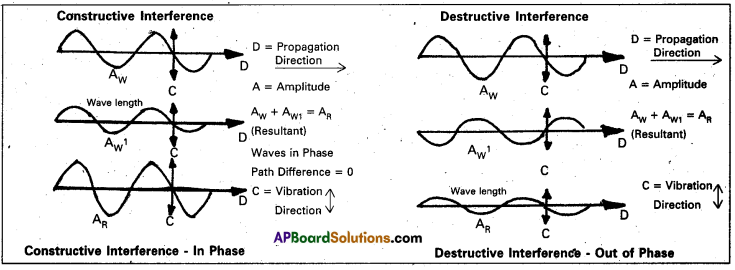
Diffraction of electromagnetic radiation takes place when a beam of light is scattered by an object containing regularly spaced lines (or) points. This scattering phenomenon can happen only if the spacing between the lines (of) points is comparable to the wave length of the radiation.
From the following figure diffraction is due to interface between two waves passing through the same region of space at the same time.
If the waves are in phase, peak to peak and trough to trough, the interference is constructive and the combined wave is increased intensity.
- If the waves are out of phase, the interference is destructive interference and the wave is cancelled.
- Constructive interference gives rise to intense spots observed on Laue’s photographic plate, while destructive interference causes the surrounding high) areas.
Derivation of Bragg’s equation : When X-rays are incident on the crystal or plane, they are diffracted from the lattice points (lattice points may be atoms or ions or molecules). In the crystal the lattice points are arranged in regular pattern. When the waves are diffracted from these points, the waves may be constructive or destructive interference.
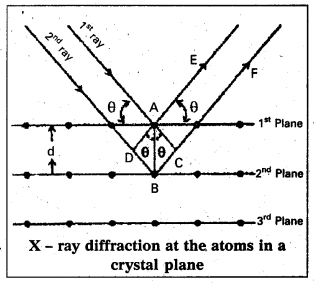
The 1st and 2nd waves reach the crystal surface. They undergo constructive interference. Then from the figure 1 and 2h1 rays are parallel waves. So, they travel the same distance till the wave front AD. The second ray travels more than the first by an extra distance (DB + BC) after crossing the grating for it to interfere with the first ray in a constructive manner. Then only they can be in the same phase with one another. If the two waves are to be in phase, the path difference between the two ways must be equal to the wavelength (λ) or integral multiple of it (nλ, where n = 1, 2, 3 )
(i.e.,) nλ = (DB + BC) [where n = order of diffraction]
DB = BC = d sin θ [θ = angle of incident beam,]
(DB + BC) = 2d sin θ [d = distance between the planes]
nλ = 2d sin θ
This relation is known as Bragg’s equation.
![]()
Textual Examples
Question 1.
A compound is formed by two elements X and Y. Atoms of the element Y (as anions) make ccp and those of the element X (as cations) occupy all the octahedral voids. What is the formula of the compound ?
Solution:
The ccp lattice is formed by the element Y. The number of octahedral voids generated would be equal to the number of atoms of Y present in it. Since all the octahedral voids are occupied by the atoms of X, their number would also be equal to that of the element Y. Thus, the atoms of elements X and Y are present in equal numbers or 1 : 1 ratio. Therefore, the formula of the compound is XY.
Question 2.
Atoms of element B form hep lattice and those of the element A occupy 2/3rd of tetrahedral voids. What is the formula of the compound formed by the elements A and B ?
Solution:
The number of tetrahedral voids formed is equal to twice the number of atoms of element B and only 2/3rd of these are occupied by the atoms of element A. Hence the ratio of the number of atoms of A and B is 2 × (2/3) : 1 or 4 : 3 and the formula of the compound is A4B3.
Question 3.
An element has a body-centred cubic (bcc) structure with a cell edge of 288 pm. The density of the element is 7.2 g/cm3. How many atoms are present in 208 g of the element ?
Solution:
Volume of the unit cell = (288 pm)3
= (288 × 10-12 m)3 = (288 × 10-10 cm)3 = 2.39 × 10-23 cm3.
Volume of 208 g of the element
= \(\frac{\text { mass }}{\text { density }}=\frac{208 \mathrm{~g}}{7.2 \mathrm{~g} \mathrm{~cm}^{-3}}\) = 28.88 cm3
Number of unit cells in this volume
= \(\frac{28.88 \mathrm{~cm}^{3}}{2.39 \times 10^{-23} \mathrm{~cm}^{3} / \text { Unit cell }}\) = 12.08 × 1023 unit cells
Since each bcc cubic unit cell contains 2 atoms, therefore, the total number of atoms in 208 g = 2 (atoms/unit cell) × 12.08 × 1023 unit cells
= 24.16 × 1023 atoms
![]()
Question 4.
X-ray diffraction studies show that copper crystallises in ah fee unit cell with cell edge of 3.608 x 10-8 cm. In a separate experiment, copper is determined to have a density of 8.92 g/cm3, calculate the atomic mass of copper.
Solution:
In case of fee lattice, number of atoms per unit cell, z = 4 atoms.
Therefore, M = \(\frac{\mathrm{dN}_{\mathrm{A}} \mathbf{a}^{3}}{z}\)
= \(\frac{8.92 \mathrm{~g} \mathrm{~cm}^{-3} \times 6.022 \times 10^{23} \text { atoms mol}^{-1} \times\left(3.608 \times 10^{-8} \mathrm{~cm}\right)^{3}}{4 \text { atoms }}\) = 63.1 g/mol
Atomic mass of copper = 63.1 u
Question 5.
Silver forms ccp lattice and X-ray studies of its ciystals show that the edge length of its unit cell is 408.6 pm. Calculate the density of silver (Atomic mass = 107.9 u).
Solution:
Since the lattice is ccp, the number of silver atoms per unit celll = z = 4
Molar mass of silver = 107.9 g mol-1 = 107.9 × 10-3 kg mol-1.
Edge length of unit cell = a = 408.6 pm = 408.6 × 10-12 m
Density, d = \(\frac{\mathrm{z} \cdot \mathrm{M}}{\mathrm{a}^{3} \cdot \mathrm{N}_{\mathrm{A}}}\)
= \(\frac{4 \times\left(107.9 \times 10^{-3} \mathrm{~kg} \mathrm{~mol}^{-1}\right)}{\left(408.6 \times 10^{-12} \mathrm{~m}\right)^{3}\left(6.022 \times 10^{23} \mathrm{~mol}^{-1}\right)}\)
= 10.5 × 103 kg m-3
= 10.5 g cm3.
Intext Questions
Question 1.
Why are solids rigid ?
Answer:
In solid state the constituent particles are not free to move. They can only oscillate about their mean positions due to strong attraction forces between the particles. That is why solids have a closely packed arrangement and rigid structure.
Question 2.
Why do solids have a definite volume ?
Answer:
The constituents particles in solids are bound to th.eir mean positions by strong forces of attraction. The interparticle distances remain unchanged even at increased or reduced pressure. Therefore, solids have a definite volume.
![]()
Question 3.
Classify the following as amorphous or crystalline solids : polyurethane, naphthalene, benzoic acid, teflon, potassium nitrate, cellophane, polyvinyl chloride, fibre glass, copper.
Answer:
Amorphous solids
Polyurethane
Naphthalene
Teflon
Cellophane
Polyvinyl chloride
Fibre glass
Crystalline solids
Benzoic acid
Potassium nitrate
Copper
Question 4.
Why is glass considered a supercooled liquid ?
Answer:
Liquids have the characteristic property i.e., the tendency to flow. Glass also shows this property, though it flows very slowly. Glass panes fixed to windows or doors of old buildings are invariably found to be slightly thicker at the bottom than the top. This is because the glass flows down very slowly and makes the bottom portion slightly thicker. Therefore, glass is considered as a supercooled liquid.
Question 5.
Refractive index of a solid is observed to have the same value along all directions. Comment on the nature of this solid. Would it show cleavage property ?
Answer:
A solid has same value of refractive index along all directions is isotropic and hence amorphous in nature. It would not show a clean cleavage when cut with a knife. Instead, it would break into pieces With irregular surface.
Question 6.
Classify the following solids in diff rent categories based on the nature of intermolecular forces operating in them :
Potassium sulphate, tin, benzene, urea, ammonia, water, zinc sulphide, graphite, rubidium, argon, silicon carbide.
Answer:
Ionic solids : Potassium sulphate, zinc sulphide (as they have iohic bonds).
Covalent solids : Graphite, silicon carbide (as they are covalent giant molecules).
Molecular solids : Benzene, urea, ammonia, water, argon (as they have covalent bond).
Metallic solids : Rubidium, tin (as these are metals).
![]()
Question 7.
Solid A’ is a very hard electrical insulator in solid as well as in molten state and melts at extremely high temperature. What type of solid is it ?
Answer:
Since, the solid ‘A’ is an insulator in solid as well as in molten state, it shows the absence of ions in it. Moreover it melts at extremly high temperature, so it is a giant molecule. These are the properties of covalent solids. So, it is a covalent solid.
Question 8.
Ionic solids conduct electricity in molten state but not in solid state. Explain.
Answer:
In ionic solids, electrical conductivity is due to the movement of ions. In solid state, ions cannot move and remain held together by strong electrostatic forces of attraction. Therefore, they behave as insulators.
Question 9.
What type of solids are electrical conductors, malleable and ductile ?
Answer:
Metallic solids.
Question 10.
Ire the significance of a ‘lattice point’.
Answer:
The lattice point denotes the position of a particular constituent (atom, ion or molecule) in a crystal lattice. The arrangement of the lattice points in space is responsible for the shape of a particular crystalline solid.
![]()
Question 11.
Name the parameters that characterise a unit cell.
Answer:
A unit cell is characterised by
- its dimensions along the three edges, a, b and c.
- angles between the edges, α (between b and c) β ( between a and c) and γ (between a and b).
Thus, a unit cell is characterised by six parameters, a, b, c, α, β and γ.
Question 12.
Distinguish between
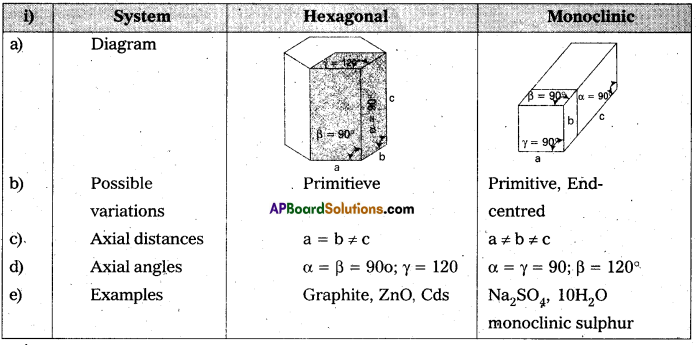
i) hexagonal and monoclinic unit cells.
ii) face-centered and end-centered unit cells.
Answer:

Question 13.
Explain how much portion of an atom located at
- Corner ?
- body-centre of a cubic unit cell is part of its neighbouring unit cell ?
Answer:
- A point lying at the corner of a unit cell is shared equally by eight unit cells and therefore,
- A body centred point belongs entirely to one unit cell since, it is not shared by any other unit cell.
Question 14.
What is the two dimensional coordination number of a molecule in square close packed layer ?
Answer:
Four (4),.as each atom is surrounded by four other atoms.
![]()
Question 15.
A compound forms hexagonal close-packed structure. What is the total number of voids in 0.5 mol of it ? How many of these are tetrahedral voids ?
Answer:
Total number of atoms (N) in a closed packed structure (0.5 mol)
= 0.5 × 6.022 × 1023 = 3.011 × 1023
Number of octahedral voids = N = 3.011 × 1023
Number of tetrahedral voids = 2N = 2 × 3.011 × 1023 = 6.022 × 1023
Total number of voids = 3.011 × 1023 + 6.022 × 1023
= 9.033 × 1023
Question 16.
A compound is formed by two elements M and N. The element N forms ccp and atoms of M occupy \(\frac{1}{3}\) rd of tetrahedral voids. What is the formula of the compound ?
i) Find the number of tetrahedral voids as number of tetrahedral voids = 2 × number of atoms present in the lattice.
ii) Calculate the number of atoms (or ratio) of elements M and N as a chemical formula represents the number of atoms of different elements presents in a compound.
iii) Derive the’ formula.
Answer:
Suppose atoms of element N present in ccp = x
Then number of tetrahedral voids = 2x
Since, \(\frac{1}{3}\) rd of the tetrahedral voids are occupied by atoms of elements M.
Therefore, number of atoms of element M = \(\frac{1}{3}\) × 2x = \(\frac{2x}{3}\)
Ratio of M : N = \(\frac{2x}{3}\) : x = 2 : 3
Hence, formula of the compound = M2N3.
Question 17.
Which of the following lattices has the highest packing efficiency ?
- Simple cubic
- Body-centred cubic
- Hexagonal close-packed lattice
Packing efficiency in .
- Simple cubic lattice = 52.4%
- body-centred cubic lattice = 68%
- hexagonal close-packed lattice = 74%
Answer:
Hexagonal closed packed lattice has the highest packing efficiency (74%)
![]()
Question 18.
An element with molar mass 2.7 × 10-2 kg mol-1 forms a cubic unit cell with edge length 405 pm. If its density is 2.7 × 103 kg m-3 what is the nature of the cubic unit cell ?
Answer:
Density (d) = \(\frac{\mathrm{Z} \times \mathrm{M}}{\mathrm{a}^{3} \times \mathrm{N}_{\mathrm{A}}}\) so, Z = \(\frac{\mathrm{d} \times \mathrm{a}^{3} \times \mathrm{N}_{\mathrm{A}}}{\mathrm{M}}\)
Given, M = 2.7 × 10-2 kg mol-1
a = 405 pm = 405 × 10-12 m = 4.05 × 10-10m
d = 2.7 × 103 kgm-3
NA = 6.022 × 1023 mol-1.
Hence.
Z = \(\frac{\left(2.7 \times 10^{3 .} \mathrm{kg} \mathrm{m}^{-3}\right)\left(4.05 \times 10^{-10} \mathrm{~m}\right)^{3} \times\left(6.022 \times 10^{23} \mathrm{~mol}^{-1}\right)}{\left(2.7 \times 10^{-2} \mathrm{~kg} \mathrm{~mol}^{-1}\right)}\)
= 3.99 = 4
Since, there are four atoms per unit cell, the cubic unit cell must be face – centred.
Question 19.
What type of defect can arise when a solid is heated ? physical property is affected by it and in what way ?
Answer:
When a solid is heated, a vacancy is created in the crystal. On heating, some of the lattice sites are vacant and the density of the solid decreases as the number of ions per unit volume decreases.
Question 20.
What type of stoichiometric defect is shown by
- ZnS
- AgBr
Answer:
- ZnS shows Frenkel defect because its ions have large difference in size.
- AgBr shows both Frenkel and Schottky defects.
Question 21.
Explain how vacancies are introduced in an ionic solid when a cation of higher valence is aded as an impurity in it ?
Answer:
When a cation of higher valence is added as an impurity to an ionic solid, some vacancies are created. This can be explained with the help of an example. When strontium, chloride (SrCl2) is added as an impurity to ionic solid sodium chloride (NaCl), two vacant sites are created by removal of one Na+ ion. One vacant site is replaced by Sr2+ ion but the other remains vacant. The reason is that the crystal as a whole is to remain electrically neutral. Note : [Cationic vacancies produced = No. of cations of higher valency × difference in ’ valencies of the original cation and cation of higher valency]
![]()
Question 22.
Ionic solids, which have anionic vacancies due to metal excess defect, develop colour. Explain with the help of a suitable example.
Answer:
We can explain the metal excess defect with the example of sodium chloride crystals. When NaCl crystals are heated in an atmosphere of sodium vapour, the Na atoms are deposited on the surface of the crystal. The Cl– ions diffuse to the surface of the crystal and combine with Na atoms to give NaCZ. This happens by loss of electron by Na atoms to form Na+ ions. The released electrons occupy anionic sites by diffusing into the crystals. These electrons absorb energy from visible light and emit radiations corresponding to yellow colour. These electrons are called F-centres (from the German word Farbenzenter meaning colour centre).
Question 23.
A group 14 elements is to be converted into n-type semiconductor by doping it with a suitable impurity. To which group should this impurity belong ?
Answer:
n-type semiconductor means increase in conductivity due to presence of excess of electrons. Therefore, a 14 group element should be doped with a 15-group element Eg : arsenic or phosphorus.
Question 24.
What type of substances would make better permanent magnets, ferromagnetic or ferrimagnetic ? Justify your answer
Answer:
Ferromagnetic substances make better permanent magnets than ferrimagnetic substances. The metal ions of a ferromagenetic substance are grouped into small regions known as domains and these are randomly oriented. When a magnetic field is applied, all domains are oriented in the direction of the magnetic field. Now the ferromagnetic substance behaves as a magnet. When the applied magnetic field is removed, the magnetic character is retained. Thus, the ferromagnetic substance becomes a permanent magnet.
This property (of being permanently magnetised) is not found in ferrimagnetic substances. They lose their magnetic property on heating.