AP State Syllabus AP Board 9th Class Maths Solutions Chapter 8 Quadrilaterals Ex 8.1 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 8th Lesson Quadrilaterals Exercise 8.1
Question 1.
State whether the statements are true or false.
i) Every parallelogram is a trapezium.
ii) All parallelograms are quadrilaterals.
iii) All trapeziums are parallelograms.
iv) A square is a rhombus.
v) Every rhombus is a square.
vi) All parallelograms are rectangles.
Solution:
i) True
ii) True
iii) False
iv) True
v) False
vi) False
![]()
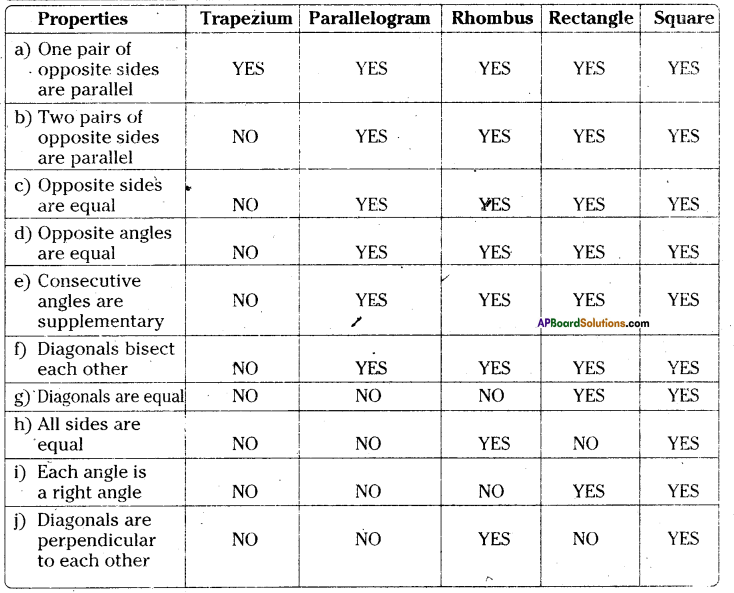
Question 2.
Complete the following table by writing YES if the property holds for the particular quadrilateral and NO if property does not holds.


Solution:
Question 3.
ABCD is a trapezium in which AB || CD. If AD = BC, show that ∠A = ∠B and ∠C = ∠D.
Solution:
Given that in □ABCD AB || CD; AD = BC
Mark a point ‘E’ on AB such DC = AE.
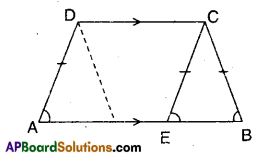
Join E, C.
Now in AECD quadrilateral
AE // DC and AE = DC
∴ □AECD is a parallelogram.
∴ AD//EC
∠DAE = ∠CEB (corresponding angles) ……………..(1)
In ΔCEB; CE = CB (∵ CE = AD)
∴ ∠CEB = ∠CBE (angles opp. to equal sides) …………….. (2)
From (1) & (2)
∠DAE = ∠CBE
⇒ ∠A = ∠B
Also ∠D = ∠AEC (∵ Opp. angles of a parallelogram)
= ∠ECB + ∠CBE [ ∵ ∠AEC is ext. angle of ΔBCE] |
= ∠ECB + ∠CEB [ ∵∠CBE = ∠CEB]
= ∠ECB + ∠ECD [∵ ∠ECD = ∠CEB alt. int. angles]
= ∠BCD = ∠C
∴ ∠C = ∠D
![]()
Question 4.
The four angles of a quadrilateral are in the ratio of 1 : 2 : 3 : 4. Find the measure of each angle of the quadri-lateral.
Solution:
Given that, the ratio of angles of a quad-rilateral = 1 : 2 : 3 : 4
Sum of the terms of the ratio
= 1 +2 + 3 + 4= 10
Sum of the four interior angles of a quadrilateral = 360°
∴ The measure of first angle
= \(\frac{1}{10}\) × 360° = 36°
The measure of second angle
= \(\frac{2}{10}\) × 360° = 72°
The measure of third angle
= \(\frac{3}{10}\) × 360° = 108°
The measure of fourth angle
= \(\frac{4}{10}\) × 360° = 144°
![]()
Question 5.
ABCD is a rectangle, AC is diagonal. Find the angles of ΔACD. Give reasons.
Solution:
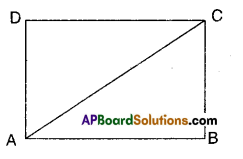
Given that □ABCD is a rectangle;
AC is its diagonal.
In ΔACD; ∠D = 90° [ ∵ ∠D is also angle of the rectangle]
∠A + ∠C = 90° [ ∵ ∠D = 90° ⇒ ∠A + ∠C = 180°-90° = 90°]
(i.e,,) ∠D right angle and
∠A, ∠C are complementary angles.
