AP State Syllabus AP Board 9th Class Maths Solutions Chapter 7 Triangles Ex 7.3 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 7th Lesson Triangles Exercise 7.3
![]()
Question 1.
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
Solution:
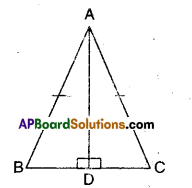
Given that in ΔABC, AB = AC
and AD ⊥ BC
i) Now in ΔABD and ΔACD
AB = AC (given)
∠ADB = ADC (given AD ⊥ BC)
AD = AD (common)
∴ ΔABD ≅ ΔACD (∵ RHS congruence)
⇒ BD = CD (CPCT)
⇒ AD, bisects BC.
ii) Also ∠BAD = ∠CAD
(CPCT of ΔABD ≅ ΔACD )
∴ AD bisects ∠A.
![]()
Question 2.
Two sides AB, BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see figure). Show that:
(i) ΔABM ≅ ΔPQN
ii) ΔABC ≅ ΔPQR
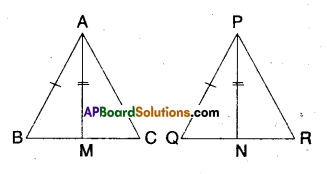
Solution:
Given that
AB = PQ
AM = PN
i) Now in ΔABM and ΔPQN
AB = PQ (given)
AM = PN (given)
BM = QN (∵ BC = QR ⇒ \(\frac { 1 }{ 2 }\)BC = \(\frac { 1 }{ 2 }\)QR ⇒ BM = QN)
∴ ΔABM ≅ ΔPQN
(∵ SSS congruence)
ii) In ΔABC and ΔPQR
AB = PQ (given)
BC = QR (given)
∠ABC = ∠PQN [∵ CPCT of ΔABM and ΔPQN from (i)]
∴ ΔABC ≅ ΔPQR
(∵ SAS congruence)
![]()
Question 3.
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Solution:
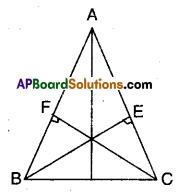
In ΔABC altitude BE and CF are equal.
Now in ΔBCE and ΔCBF
∠BEC = ∠CFB (∵ given 90°)
BC = BC (common; hypotenuse)
CF = BE (given)
∴ ΔBEC ≅ ΔCBF
⇒ ∠EBC = ∠FCB (∵ CPCT)
But these are also the interior angles opposite to sides AC and AB of ΔABC.
⇒ AC = AB
Hence proved.
![]()
Question 4.
ΔABC is an isosceles triangle in which AB = AC. Show that ∠B = ∠C.
(Hint : Draw AP ⊥ BQ (Using RHS congruence rule)
Solution:
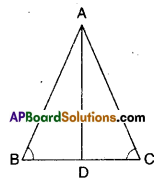
Given the ΔABC is an isosceles triangle and AB = AC
Let D be the mid point of BC; Join A, D.
Now in ΔABD and ΔACD
AB = AC (given)
BD = DC (construction)
AD = AD (common)
∴ ΔABD ≅ ΔACD (∵ SSS congruence)
⇒ ∠B = ∠C [∵ CPCT]
Question 5.
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see figure). Show that ∠BCD is a right angle.
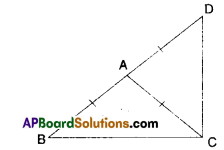
Solution:
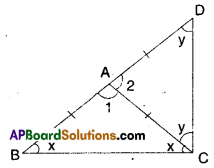
Given that in ΔDBC; AB = AC; AD = AB
In ΔABC
∠ABC + ∠ACB = ∠DAC …………… (1)
[∵ exterior angle]
In ΔACD
∠ADC + ∠ACD = ∠BAC ………………(2)
Adding (1) & (2)
∠DAC + ∠BAC = 2 ∠ACB + 2∠ACD
[∵ ∠ABC = ∠ACB
∠ADC = ∠ACD]
180° = 2 [∠ACB + ∠ACD]
180° = 2[∠BCD]
∴ ∠BCD = \(\frac{180^{\circ}}{2}\) = 90°
(or)
From the figure
∠2 = x + x = 2x
∠1 = y + y = 2y
∠1 + ∠2 = 2x + 2y
180° = 2 = (x + y)
∴ x + y = \(\frac{180^{\circ}}{2}\) = 90°
Hence proved.
![]()
Question 6.
ABC is a right angled triangle in which ∠A = 90° and AB = AC, Show that ∠B = ∠C.
Solution:
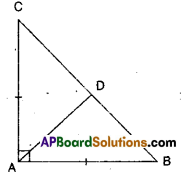
Given ΔABC; AB – AC
Join the mid point D of BC to A.
Now in ΔADC and ΔADB
AD = AD (common)
AC = AB (giyen)
DC = DB (construction)
⇒ ΔADC ≅ ΔADB
⇒ ∠C = ∠B (CPCT)
![]()
Question 7.
Show that the angles of an equilateral triangle are 60° each.
Solution:
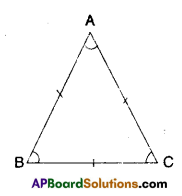
Given ΔABC is an equilateral triangle
AB = BC = CA
∠A = ∠B (∵ angles opposite to equal sides)
∠B = ∠C (∵ angles opposite to equal sides)
⇒ ∠A = ∠B = ∠C = x say
Also ∠A+∠B + ∠C =180°
⇒ x + x + x = 180°
3x = 180°
⇒ x = \(\frac{180}{3}\) = 60°
Hence proved.
