AP State Syllabus AP Board 9th Class Maths Solutions Chapter 4 Lines and Angles Ex 4.2 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 4th Lesson Lines and Angles Exercise 4.2
![]()
Question 1.
In the given figure three lines \(\overline{\mathrm{AB}}\) , \(\overline{\mathrm{CD}}\) and \(\overline{\mathrm{EF}}\) intersecting at ‘O’. Find the values of x, y and z, it is being given that x : y : z = 2 : 3 : 5
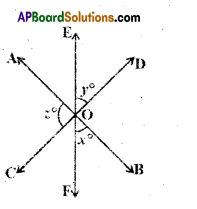
Solution:
From the figure
2x + 2y + 2z = 360°
⇒ x + y + z = 180°
x : y : z = 2 : 3 : 5
Sum of the terms of the ratio
= 2 + 3 + 5 = 10

![]()
Question 2.
Find the value of x in the following figures.
i)
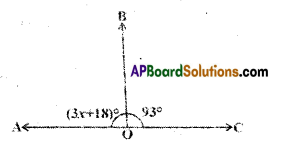
Solution:
From the figure
3x + 18= 180° – 93° (∵ linear pair )
3x + 18 = 87
3x = 87- 18 = 69
∴ x = \(\frac{69}{3}\) = 23
ii)
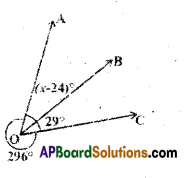
Solution:
From the figure
(x – 24)° + 29° + 296° = 360“
(∵ complete angle)
x + 301° = 360°
∴ x = 360° – 301° = 59°
iii)
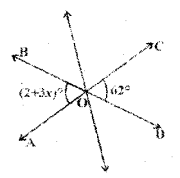
Solution:
From the figure
2 + 3x = 62
(∵ vertically opposite angles)
3x = 62 – 2
∴ 3x = 60° ⇒ x = \(\frac{60}{3}\)
∴ x = 20°
![]()
iv)
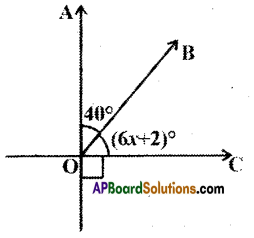
Solution:
From the figure
40 + (6x + 2) = 90°
(∵ complementary angles)
6x = 90° – 42°
6x = 48
x = \(\frac{48}{6}\) = 8°
Question 3.
In the given figure lines \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{CD}}\) intersect at ’O’. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.
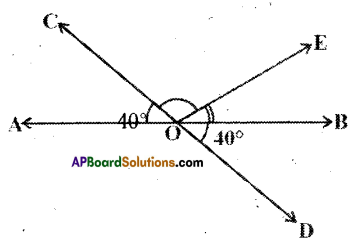
Solution:
Given that ∠AOC +∠BOE = 70°
∠BOD = 40°
∠AOC = 40°
(∵ ∠AOC, ∠BOD are vertically opposite angles)
∴ 40° + ∠BOE = 70°
⇒ ∠BOE = 70° – 40° = 30°
Also ∠AOC + ∠COE +∠BOE = 180°
( ∵ AB is a line)
⇒ 40° + ∠COE + 30° = 180°
⇒ ∠COE = 180° -70° = 110°
∴ Reflex ∠COE = 110°
![]()
Question 4.
In the given figure lines \(\overline{\mathrm{XY}}\) and \(\overline{\mathrm{MN}}\) . intersect at O. If ∠POY = 90° and a : b = 2:3, find c.
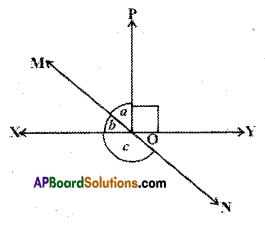
Solution:
Given that XY and MN are lines.
∠POY = 90°
a : b = 2 : 3
From the figure a + b = 90°
Sum of the terms of the ratio a : b
= 2 + 3 = 5
∴ b = \(\frac{3}{5}\) x 90° = 54°
From the figure b + c = 180°
(∵ linear pair of angles)
54° + c = 180°
c = 180°-54° = 126°
![]()
Question 5.
In the given figure ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.
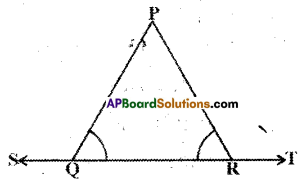
Solution:
Given that ∠PQR = ∠PRQ
From the figure
∠PQR + ∠PQS = 180° ………….. (1)
∠PRQ + ∠PRT = 180° …………..(2)
From (1) and (2)
∠PQR + ∠PQS = ∠PRQ + ∠PRT
But ∠PQR = ∠PRQ
So ∠PQS = ∠PRT
Hence proved.
Question 6.
In the given figure, if x + y = w + z, then prove that AOB is a line.
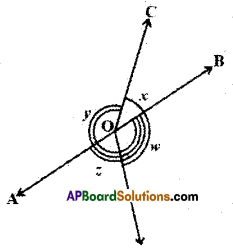
Solution:
Given that x + y = w + z = k say
From the figure
x + y + z + w = 360°
(∵ Angle around a point)
Also x + y = z + w
∴ x + y = z + w = \(\frac{360^{\circ}}{2}\)
∴ x + y = z + w = 180°
OR
k + k = 360°
2k = 360°
k = \(\frac{360^{\circ}}{2}\)
(i.e.) (x,y) and (z, w) are pairs of adjacent angles whose sum is 180°.
In other words (x, y) and (z, w) are linear pair of angles ⇒ AOB is a line.
![]()
Question 7.
In the given figure \(\overline{\mathrm{PQ}}\) is a line. Ray \(\overline{\mathrm{OR}}\) is perpendicular to line \(\overline{\mathrm{PQ}}\).\(\overline{\mathrm{OS}}\) os is another ray lying between rays \(\overline{\mathrm{OP}}\) and \(\overline{\mathrm{OR}}\) Prove that
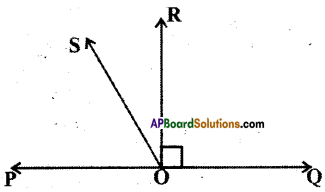
Solution:
Given : OR ⊥ PQ ⇒ ∠ROQ = 90°
To prove: ∠ROS = \(\frac{1}{2}\) (∠QOS – ∠POS)
Solution:
Proof: From the figure
∠ROS = ∠QOS – ∠QOR ……………(1)
∠ROS = ∠ROP – ∠POS ……………..(2)
Adding (1) and (2)
∠ROS + ∠ROS = ∠QOS – ∠QOR +∠ROP – ∠POS [ ∵ ∠QOR = ∠ROP = 90° given]
⇒ 2∠ROS = ∠QOS – ∠POS
⇒ ∠ROS = \(\frac{1}{2}\) [∠QOS – ∠POS]
Hence proved.
![]()
Question 8.
It is given that ∠XYZ = 64° and XY is produced to point P. A ray \(\overline{\mathrm{YQ}}\) bisects ∠ZYP. Dräw a figure from the given Information. Find ∠XYQ and reflex ∠QYP.
Solution:
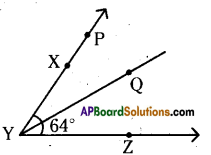
∠XYQ = 32°
∠QYP = 32°
