AP State Syllabus AP Board 9th Class Maths Solutions Chapter 2 Polynomials and Factorisation InText Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 2nd Lesson Polynomials and Factorisation InText Questions
![]()
Think, Discuss and Write
Question
Which of the following expressions are polynomials ? Which are not ? Give reasons. [Page No. 28]
Solution:
i) 4x2 + 5x – 2 is a polynomial.
ii) y2 – 8 is a polynomial.
iii) 5 is a constant polynomial.
iv) \(2 x^{2}+\frac{3}{x}-5\) is not a polynomial as x is in denominator.
v) √3x2 + 5y is a polynomial.
vi) \(\frac{1}{x+1}\) is not a polynomial as the variable x is in denominator.
vii) √x is not a polynomial as its exponent is not an integer.
viii) 3xyz is a polynomial.
![]()
Do These
Question
Write two polynomials with variable ‘x’. [Page No. 29]
Solution:
5x2 + 2x – 8 and 3x2 – 2x + 6.
Question
Write three polynomials with variable ‘y’.
Solution:
y3 – y2 + y ; 2y2 + 7y – 9 + 3y3; y4 – y + 6 + 2y2.
Question
Is the polynomial 2x2 + 3xy + 5y2 in one variable ?
Solution:
No. It is in two variables x and y.
![]()
Question
Write the formulae of area and volume of different solid shapes. Find out the variables and constants in them. [Page No. 29]
Solution:
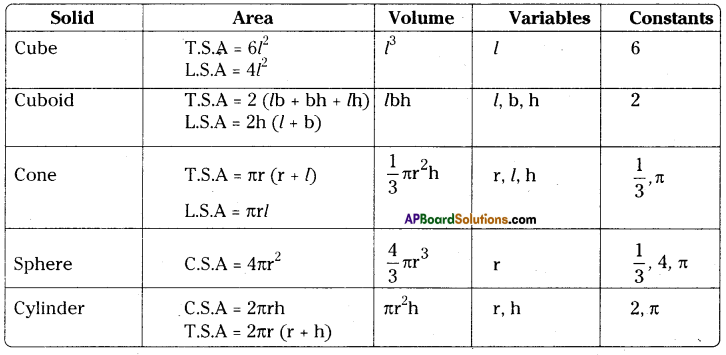
Question 1.
Write the degree of each of the following polynomials. [Page No. 30]
Solution:
i) 7x3 + 5x2 + 2x – 6 – degree 3
ii) 7 – x + 3x2 – degree 2
iii) 5p – √3 – degree 1
iv) 2 – degree 0
v) – 5 xy2 – degree 3
![]()
Question 2.
Write the co-efficient of x2 in each of the following. [Page No. 30]
Solution:
i) 15 – 3x + 2x2 : co-efficient of x2 is 2
ii) 1 -x2 : co-efficient of x2 is -1
iii) πx2 – 3x + 5 : co-efficient of x2 is π
iv) √2x2 + 5x – 1 : co-efficient of x2 is √2
Think, Discuss and Write
Question
How many terms a cubic (degree 3) polynomial with one variable can have? Give examples. [Page No. 31]
Solution:
A cubic polynomial can have atmost 4 terms.
E.g.: 5x3 + 3x2 – 8x + 4; x3 – 8
Try These
Question 1.
Write a polynomial with 2 terms in variable x. [Page No. 31]
Solution:
2x + 3x2
![]()
Question 2.
How can you write a polynomial with 15 terms in variable ‘x’. [Page No. 31]
Solution:
a14p14 + a13p13 + a12p12+ …………….+ a1p + a0
Do This
Question
Find the value of each of the follow ing polynomials for the indicated value of variables. [Page No. 33]
(i) p(x) = 4x2 – 3x + 7 at x = 1.
Solution:
The value of p(x) at x = 1 is
4(1)2 – 3(1) + 7 = 8
ii) q(y) = 2y3 – 4y + √11 at y = 1.
Solution:
The value of q(y) at y = 1 is
2(1)3 – 4(1) + √11 = -2 + √11
iii) r(t) = 4t4 + 3t3 – t2 + 6 at t = p, t ∈ R.
Solution:
The value of r(t) at t = p is
4p4 + 3p3 – p2 + 6
![]()
iv) s(z) = z3 – 1 at z – 1.
Solution:
The value of s(z) at z = 1 is 13 – 1 = 0
v) p(x) = 3x2 + 5x – 7 at x = 1.
Solution:
The value of p(x) at x = 1 is
3(1)2 + 5(1) — 7 = 1.
vi) q(z) = 5z3 – 4z + √2 at 7. = 2.
Solution:
The value of q(z) at z = 2 is
5(2)3 – 4(2) + √2 = 40 – 8 + √2
= 32 + √2
![]()
Try These
Question
Find zeroes of the following polyno¬mials. [Page No. 34]
1. 2x-3
Solution:
2x – 3 = 0
2x = 3
x = \(\frac{3}{2}\)
∴ x = \(\frac{3}{2}\) is the zero of 2x – 3.
2. x2 – 5x + 6
Solution:
x2 – 5x + 6 = 0
⇒ x2 – 3x – 2x + 6 = 0
⇒ x (x – 3) – 2 (x – 3) = 0
⇒ (x – 2) (x – 3) = 0
⇒ x – 2 = 0 or x – 3 = 0
⇒ x = 2 or x = 3
∴ x = 2 or 3 are the zeroes of x2 – 5x + 6.
![]()
3. x + 5
Solution:
x + 5 = 0
x = – 5
∴ x = – 5
Do This
Fill in the bianks : [Page No. 35]
| Linear polynomial | Zero of the polynomial |
| x + a | – a |
| x – a | a |
| ax + b | \( \frac{-b}{a} \) |
| ax – b | \( \frac{b}{a} \) |
Solution:
| Linear polynomial | Zero of the polynomial |
| x + a | – a |
| x – a | a |
| ax + b | \( \frac{-b}{a} \) |
| ax – b | \( \frac{b}{a} \) |
Think, and Discuss
Question 1.
x2 + 1 has no zeroes. Why ? [Page No. 36]
Solution:
x2 + 1 = 0 ⇒ x2 = -1
No real number exists such that whose root is – 1.
∴ x2 + 1 has no zeroes.
![]()
Question 2.
Can you tell the number of zeroes of a polynomial of degree ‘n’ will have? [Page No. 36]
Solution:
A polynomial of degree n will have n- zeroes.
Do These
Question 1.
Divide 3y3 + 2y2 + y by ‘y’ and write division fact. [Page No. 38]
Solution:
(3y3 + 2y2 + y) ÷ y = \(\frac{3 y^{3}}{y}+\frac{2 y^{2}}{y}+\frac{y}{y}\)
= 3y2 + 2y + 1
Division fact = (3y2 + 2y + 1) y
= 3y3 + 2y2 + y
![]()
Question 2.
Divide 4p2 + 2p + 2 by ‘2p’ and write division fact.
Solution:
4p2 + 2p ÷ 2 = \(\frac{4 p^{2}}{2 p}+\frac{2 p}{2 p}+\frac{2}{2 p}\)
= 2p + 1 + \(\frac{1}{\mathrm{P}}\)
Division fact:
(2p + 1 + \(\frac{1}{\mathrm{P}}\)).2p = 4p2 + 2p + 2
Try These
Show that (x – 1) is a factor of xn – 1. [Page No. 45]
Solution:
Let p(x) = xn – 1
Then p(1) = 1n – 1 = 1 – 1 = 0
As p(1) = 0, (x – 1) is a factor of p(x).
Do These
Question
Factorise the following. [Page No. 46]
1. 6x2 + 19x + 15
Solution:
6x2 + 19x + 15 = 6x2 + 10x + 9x + 15
= 2x (3x + 5) + 3 (3x + 5)
= (3x + 5) (2x + 3)
![]()
2. 10m2 – 31m – 132
Solution:
10m2 – 31m – 132
= 10m2 – 55m + 24m – 132
= 5m (2m- 11) + 12 (2m- 11)
= (2m – 11) (5m + 12)
3. 12x2 + 11x + 2
Solution:
12x2 + 11x + 2
= 12x2 + 8x + 3x + 2
= 4x (3x + 2) + 1 (3x + 2)
= (3x + 2) (4x + 1)
![]()
Try This
Question
Try to draw the geometrical figures for other identities. [Page No. 49]
i) (x + y)2 ≡ x2 + 2xy + y2
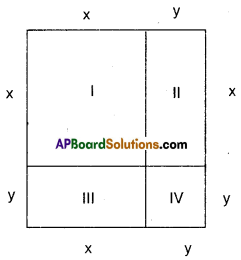
Step – 1 : Area of fig. I = x x = x2
Step – 2 : Area of fig. II = x y = xy
Step – 3 : Area of fig. III = x y = xy
Step – 4 : Area of fig. IV = y y = y2
Area of big square = sum of the areas of figures I, II, III and IV
∴ (x + y) (x + y) = x2 + xy + xy + y2
(x + y)2 = x2 + 2xy + y2
ii) (x + y) (x – y) ≡ x2 – y2
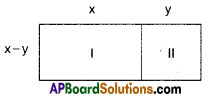
Step -1: Area of fig! I = x (x – y) = x2 – xy
Step – 2: Area of fig. II = (x – y) y = xy – y2
Area of big rectangle = sum of areas of figures I & II
(x + y) (x – y) = x2 – xy + xy – y2
= x2 – y2
∴ (x + y) (x-y) = x2-y2
![]()
iii) (x + a) (x + b) ≡ x2 + (a + b) x + ab

Step – 1 : Area of fig. I = x2
Step – 2 : Area of fig. II = ax
Step – 3 : Area of fig. Ill = bx
Step – 4 : Area of fig. IV = ab
∴ Area of big rectangle = Sum of areas of four small figures.
∴ (x + a) (x + b) = x2 + ax + bx + ab
(x + a) (x + b) = x2 + (a + b) x + ab
Do These
Question
Find the following product using appropriate identities. [Page No. 49]
i) (x + 5) (x + 5)
Solution:
(x + 5) (X + 5) = (x + 5)2
= x2 + 2(x) (5) + 52
= x2 + 10x + 25
ii) (p – 3) (p + 3)
Solution:
(p – 3) (p + 3)
= p2 – 32
= p2 – 9
iii) (y – 1) (y – 1)
Solution:
(y – 1) (y – 1)
= (y – 1)2
= y2 – 2y + 1
![]()
iv) (t + 2) (t + 4)
Solution:
(t + 2) (t + 4)
= t2 + t(2 + 4) + 2 x 4
= t2 + 6t + 8
v) 102 x 98
Solution:
102 x 98 = (100 + 2) (100 -2)
= 1002 – 22
= 10000 – 4
= 9996
![]()
Do These
Question
Factorise the following using appro-priate identities. [Page No. 50]
i) 49a2 + 70ab + 25b2
Solution:
49a2 + 70ab + 25b2
= (7a)2 + 2 (7a) (5b) + (5b)2
= (7a + 5b)2
= (7a + 5b)(7a + 5b)
ii) \(\frac{9}{16} x^{2}-\frac{y^{2}}{9}\)
Solution:

iii) t2 – 2t + 1
= (t)2 – 2(t) (1) + (1)2
= (t – 1)2 = (t – 1) (t – 1)
iv) x2 + 3x + 2
Solution:
x2 + 3x + 2 = x2 + (2 + 1) x + (2 x 1)
(x + 2) (x + 1)
![]()
Do These
Question i)
Write (p + 2q + r)2 in expanded form. [Page No. 52]
Solution:
(p + 2q + r)2 = (p)2 + (2q)2 + (r)2
+ 2 (P) (2q) + 2 (2q) (r) + 2(r) (p)
= p2 + 4q2 + r2 + 4pq + 4qr + 2rp
Question ii)
Expand (4x – 2y – 3z)2 using identity. [Page No. 52]
Solution:
(4x – 2y – 3z)2 = (4x)2 + (- 2y)2 + (- 3z)2 + 2 (4x) (- 2y) + 2 (- 2y) (- 3z) + 2 (- 3z) (4x)
= 16x2 + 4y2 + 9z2 – 16xy + 12yz – 24zx.
Question iii)
Factorise 4a2 + b2 + c2 – 4ab + 2bc – 4ca
using identity. [Page No. 52]
Solution:
4a2 + b2 + c2 – 4ab + 2bc – 4ca
= (2a)2 + (- b)2 + (- c)2 + 2(2a) (- b) + 2 (- b) (- c) + 2(- c) (2a)
= (2a – b – c)2 = (2a – b – c) (2a – b – c)
![]()
Try These
Question
How can you find (x – y)3 without actual multiplication ? Verify with actual multiplication. [Page No. 52]
Solution:
(x – y)3 = x3 – 3x2y + 3xy2 – 3y3 from identity.
By actual multiplication
(x – y)3 = (x – y)2 (x – y)
= (x2 – 2xy + y2) (x – y)
= x3 – 2x2y + xy2 – x2y + 2xy2 – y3
= x3 – 3x2 y + 3xy2 – y3
Both are equal.
Do These
Question 1.
Expand (x + 1)3 using an identity. [Page No. 54]
Solution:
(x + 1)3 = (x)3 + (1)3 + 3 (x) (1) (x + 1)
= x3 + 1 + 3x (x + 1)
= x3 + 1 + 3x2 + 3x = x3 + 3x2 + 3x + 1
Question 2.
Compute (3m – 2n)3. [Page No. 54]
Solution:
(3m-2n)3
=(3m)3 – 3 (3m)2 (2n) + 3 (3m) (2n)2 – (2n)3
= 27m3 – 54m2n + 36mn2 – 8n3
![]()
Question 3.
Factorise a3 – 3a2b + 3ab2 – b3. [Page No. 54]
Solution:
a3 – 3a2b + 3ab2 – b3
= (a)3 – 3 (a)2 (b) + 3 (a) (b)2 – (b)3
= (a – b)3
= (a – b) (a – b) (a – b)
Do These
Question 1.
Find the product (a – b – c) (a2 + b2 + c2 – ab + be – ca) without actual multi-plication. [Page No. 55]
Solution:
The problem is incorrect.
![]()
Question 2.
Factorise 27a3 + b3 + 8c3 – 18abc using identity. [Page No. 55]
Solution:
27a3 + b3 + 8c3 – 18abc
= (3a)3 + (b)3 + (2c)3 – 3(3a) (b) (2c)
= (3a + b + 2c) (9a2 + b2 + 4c2 – 3ab – 2be – 6ca)
