AP State Syllabus AP Board 9th Class Maths Solutions Chapter 2 Polynomials and Factorisation Ex 2.3 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 2nd Lesson Polynomials and Factorisation Exercise 2.3
Question 1.
Find the remainder when
x3 + 3x2 + 3x + 1 is divided by the following Linear polynomials i) x + 1 Each
Solution:
Let f(x) = x3 + 3x2 + 3x + 1
By remainder theorem, the remainder is f (- 1)
f (- 1) = (- 1)3 + 3(- 1)2 + 3(- 1) + 1
= – 1 + 3 – 3 + 1 = 0
![]()
ii) \(x-\frac{1}{2}\)
f(x) = x3 + 3x2 + 3x + 1
By remainder theorem, the remainder is \(\mathrm{f}\left(\frac{1}{2}\right)\)

iii) x
Solution:
f(x) = x3 + 3x2 + 3x + 1
The remainder is f(0)
∴ f(0) = 03 + 3(0)2 + 3(0) + 1 = 1
iv) x + π
Solution:
f(x) = x3 + 3x2 + 3x + 1
By remainder theorem, the remainder is f(- π)
f(- π) = (- π)3 + 3(-π)2 + 3 (-π) + 1 .
= – π3 + 3π2 – 3π + 1
v) 5 + 2x
f(x) = x3 + 3x2 + 3x + 1
The remainder is \(\mathrm{f}\left(\frac{-5}{2}\right)\)

![]()
Question 2.
Find the remainder when x3 – px2 + 6x – p is divided by x – p.
Solution:
Let f(x) = x3 – px2 + 6x – p
(x – a) = x – p)
By Remainder theorem, the remainder is f(p)
∴ f(P) = P3 – P(P)2 + 6p – p
= p3 – p3 + 5p = 5p
Question 3.
Find the remainder when 2x2 – 3x + 5 is divided by 2x – 3. Does it exactly divide the polynomial ? State reason.
Solution:
Let f(x) = 2x2 – 3x + 5 and
x – a = 2x – 3 = x – \(\frac{3}{2}\)
By Remainder theorem f(x) when divided by (x – \(\frac{3}{2}\) ) leaves a remainder \(\mathrm{f}\left(\frac{3}{2}\right)\)
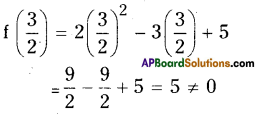
As the remainder is 5 we say that (2x – 3) is not a factor of f(x).
Question 4.
Find the remainder when 9x3 – 3x2 + x – 5 is divided by x – \(\frac{2}{3}\)
Solution:
Let f(x) = 9x3 – 3x2 + x – 5
x-a = x – \(\frac{2}{3}\)
Remainder theorem the remainder is \(\mathrm{f}\left(\frac{2}{3}\right)\)
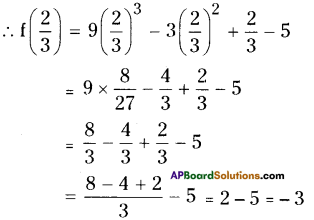
![]()
Question 5.
If the polynomials 2x3 + ax2 + 3x – 5 and x3 + x2 – 4x + a leave the same remainder, when divided by x – 2, find the value of a.
Solution:
Let f(x) = 2x3 + ax2 + 3x – 5
g(x) = x3 + x2 – 4x + a
Given that f(x) and g(x) divided x – 2
give same remainder.
i e., f(2) = g(2)
By Remainder theorem.
But f(2) = 2(2)3 + a(2)2 + 3(2) – 5
= 2 x 8 + 4a + 6 – 5
= 17 +4a
g(2) = 23 + 22 – 4(2) + a .
= 8 + 4 – 8 + a = 4 + a
i.e., 4 + a = 17 + 4a
∴ a – 4a = 17 – 4
– 3a = 13
a = -13/3
Question 6.
If the polynomials x3 + ax2 + 5 and x3 – 2x2 + a are divided by (x + 2) leave the same remainder, find the value of a.
Solution:
Let f(x) = x3 + ax2 + 5
g(x) = x3 – 2x2 + a
Given that when f(x) and g(x) divided by (x + 2) leaves the same remainder.
i.e.,f(-2) = g(-2)
By Remainder theorem
f(- 2) = (- 2)3 + a(- 2)2 + 5
= -8 + 4a + 5 = 4a – 3
g(- 2) = (- 2)3 – 2(- 2)2 + a
= -8 – 8 + a = a – 16
By problem,
4a – 3 = a – 16
4a – a = – 16 + 3
⇒ 3a = – 13 ⇒ a = -13/3
![]()
Question 7.
Find the remainder when f(x) = x4 – 3x2 + 4 is divided by g(x) = x – 2 and verify the result by actual division.
Solution:
Given f(x) = x4 – 3x2 + 4
g(x) = x – 2
The remainder when f(x) is divided by g(x) is f(2).
f(2) = 24 – 3(2)2 + 4
= 16 – 12 + 4
= 8
Actual division

∴ The remainder either by Remainder theorem or by actual division is the same.
Question 8.
Find the remainder when p(x) = x3 – 6x2 + 14x – 3 is divided by g(x) = 1 – 2x and verify the result by long division method.
Solution:
Given p(x) = x3 – 6x2 + 14x – 3
g(x) = 1 – 2x
By Remainder theorem when p(x) is divided by g(x) is p(1/2).

![]()
Question 9.
When a polynomial 2x3 + 3x2 + ax + b is divided by (x – 2) leaves remainder 2, and (x + 2) leaves remainder – 2. Find a and b.
Solution:Let f(x) = 2x3 + 3x2 + ax + b
The remainder when f(x) is divided by (x – 2) is 2.
i.e., f(2) = 2
⇒ 2(2)3 + 3(2)2+ a(2) + b = 2
⇒ 16 + 12 + 2a +b = 2
⇒ 2a + b = – 26 …………………..(1)
Also the remainder when f(x) is divided by (x + 2) is – 2.
i.e., f(- 2) = – 2
⇒ 2(- 2)3 + 3(- 2)2 + a (- 2) + b = – 2
⇒ -16 + 12 – 2a + b = – 2
– 2a + b = 2 ………………..(2)
Solving (1) and (2),
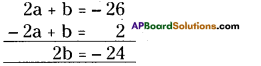
b = – 12
and 2a – 12 = – 26
2a = -26+ 12
a = -14/2 = -7,
a = -7, b = – 12
