Students can go through AP Board 9th Class Maths Notes Chapter 10 Surface Areas and Volumes to understand and remember the concepts easily.
AP State Board Syllabus 9th Class Maths Notes Chapter 10 Surface Areas and Volumes
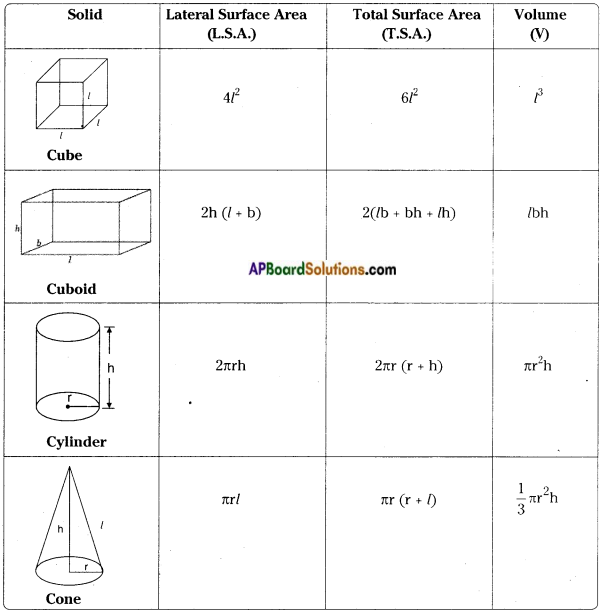
→ Cuboid and cube may be treated as regular prisms having six faces.

![]()
→ Solids whose lateral surfaces are parallelograms are called prisms,
→ Solids whole lateral surfaces are triangles are called pyramids.
→ Cube and cuboid are also prisms.
→ Volume of a pyramid = \(\frac{1}{3}\) Area of the base × height
= \(\frac{1}{3}\) of the volume of right prism.