AP State Syllabus AP Board 8th Class Maths Solutions Chapter 6 Square Roots and Cube Roots Ex 6.2 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 6th Lesson Square Roots and Cube Roots Exercise 6.2
![]()
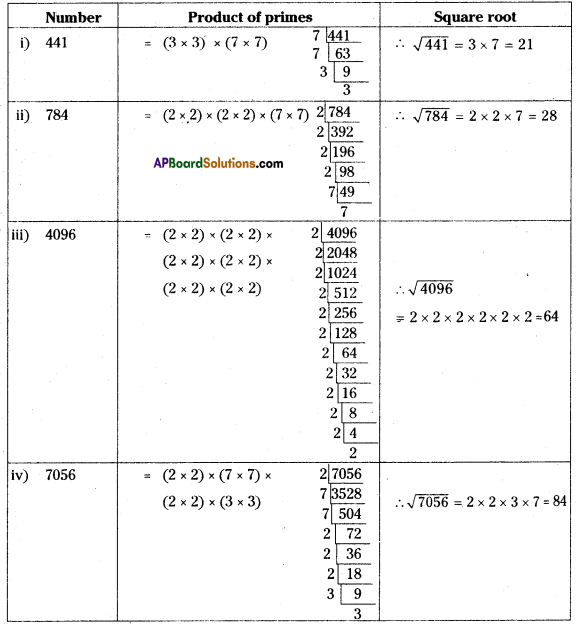
Question 1.
Find the square roots of the following numbers by Prime factorization method.
(1) 441
(ii) 784
(iii) 4096
(iv) 7056
Solution:
![]()
Question 2.
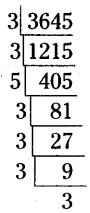
Find the smallest number by which 3645 must be multiplied to get a perfect square.
Solution:
The prime factorization of 3645
= (3 × 3) × (3 × 3) (3 × 3) × 5
∴ Deficiency of one ‘5’ is appeared in the above product.
∴ 3645 is multiplied with 5 then we will get a perfect square.
Question 3.
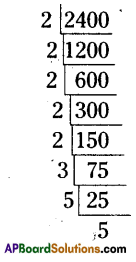
Find the smallest number by which 2400 is to be multiplied to get a perfect square and also find the square root of the resulting number.
Solution:
The prime factorization of 2400
=(2 × 2) × (2 × 2) × 2 × (5 × 5) × 3
∴ 2,3 are needed to form a pair
∴ 2 × 3 = 6
∴ 6 should be multiplied with 2400 then we will get a perfect square number.
∴ 2400 × 6 = 14400
∴ \(\sqrt{14400}\) = 120
![]()
Question 4.
Find the smallest number by which 7776 is to be divided to get a perfect square.
Solution:
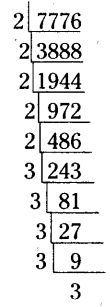
The prime factorization of 7776
=(2 × 2) × (2 × 2) × 2 × (3 × 3) × (3 × 3) × 3
∴ 2, 3 are needed to form a pair
∴ 2 × 3 = 6
∴ 7776 should be divided by 6 then we will get a perfect square number.
![]()
Question 5.
1521 trees are planted in a garden in such a way that there are as many trees in each row as there are rows in the garden. Find the number of rows and number of trees in each row.
Solution:
Let the no. of trees planted in a garden for each row = x say.
No. of rows in the garden = x
∴ Total no. of trees in the garden = x × x = x2
According to the sum x2 = 1521
x = \(\sqrt{1521}=\sqrt{39 \times 39}\) = 39
∴ No. of trees for each row = 39
No. of rows in the garden = 39
Question 6.
A school collected ₹ 2601 as fees from its students. If fee paid by each student and number students in the school were equal, how many students were there in the school?
Solution:
Let the no. of students in a school = x say
The (amount) fee paid by each student = ₹ x
Amount collected by all the students
= x × x = x2
According to the sum
∴ x2 = 2601
x = \(\sqrt{2601}=\sqrt{51 \times 51}\) = 51
∴ x = 51
∴ No. of students in the school = 51
Question 7.
The product of two numbers is 1296. If one number is 16 times the other, find the two numbers?
Solution:
Given that the product of two numbers = 1296.
Let the second number = x say
Then first number = 16 × x = 16x
∴ The product of two numbers
= x × 16x= 16x2
According to the sum
16x2 = 1296
⇒ x2 = \(\frac { 1296 }{ 16 }\) = 81
⇒ x2 = 81
⇒ x = \(\sqrt{8} \overline{1}=\sqrt{9 \times 9}\) = 9
⇒ x = 9
∴ The first number = 16x
= 16 × 9
=144
The second number = x = 9
![]()
Question 8.
7921 soldiers sat in an auditorium in such a way that there are as many soldiers in a row as there are rows in the auditorium. How many rows are there in the auditorium’?
Solution:
Let the number of soldiers sat in an auditorium for each row = x say
∴ No. of rows in an auditorium = x
∴ Total no. of soldiers = x × x = x2
According to the sum,
x2 = 7921
x = \(\sqrt{7921}=\sqrt{89 \times 89}\) = 89
∴ No. of rowS in an auditorium = 89
Question 9.
The area of a square field is 5184 m2. Find the area of a rectangular field, whose perimeter is equal to the perimeter of the square field and whose length is twice of its breadth.
Solution:
Area of a square field = 5184 m2
A = s2 = 5184
:. s = \(\sqrt{5184}=\sqrt{72 \times 72}\) = 72
∴ s = 72
∴ Perimeter of the square field = 4 × s
= 4 × 72
= 288 m
According to the sum,
Perimeter of a rectangular field
= Perimeter of a square field = 288 m
Let the breadth of a rectangular field
= x m say
∴ Length = 2 × x = 2 × m
∴ Perimeter of the rectangular field
= 2 (1 + b)
= 2 (2x + x)
= 2 × 3x
= 6x
∴ 6x = 288 .
x = \(\frac { 288 }{ 6 }\)
x = 48
∴ Breadth of the rectangular field
= x = 48 m
Length of the rectangular field = 2x
= 2 × 48
=96m
∴ Area of the rectangular field
= l × b
= 96 × 48
= 4608 m2
