AP State Syllabus AP Board 7th Class Maths Solutions Chapter 9 Construction of Triangles Ex 2 Textbook Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 9th Lesson Construction of Triangles Exercise 2
![]()
Question 1.
Draw ΔCAR in which CA = 8 cm, ∠A = 60° and AR = 8 cm. Measure CR, ∠R and ∠C. What kind of triangle is this?
Solution:
CA = 8 cm, ∠A = 60°, AR = 8 cm
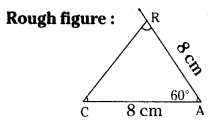
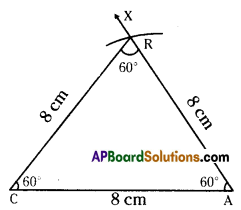
Step. -1: Draw a rough sketch of a triangle and label it with the given measurements.
Step -2: Draw a line segment CA of length 8 cm.
Step -3: Draw a ray \(\overrightarrow{\mathrm{AX}}\) making an angle 60° with CA.
Step -4: Draw an arc of radius 8 cm fromA which cuts \(\overrightarrow{\mathrm{AX}}\) at C.
Step -5: Join C, R to get the required
Δ CAR. CR = 8 cm, ∠C = 60° and ∠R = 60°.
∴ This is an equilateral triangle.
![]()
Question 2.
Construct ΔABC in which AB = 5cm, ∠B = 45° and BC = 6cm.
Solution:
AB = 5cm, ∠B = 45° and BC = 6cm.
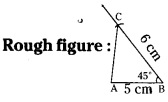
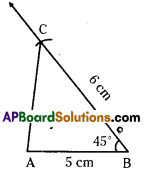
Step -1: Draw a rough sketch of a triangle and label it with the given measurements.
Step -2: Draw a line segment AB of length 5cm.
Step -3: Draw a ray \(\overrightarrow{\mathrm{BY}}\) making an angle 45° with AB.
Step -4: Draw an arc of radius 6 cm from B, which cuts \(\overrightarrow{\mathrm{BY}}\) at C.
Step -5: Join A, B to get the required ΔABC.
Question 3.
Construct ΔPQR such that ∠R = 100°, QR = RP = 5.4 cm.
Solution:
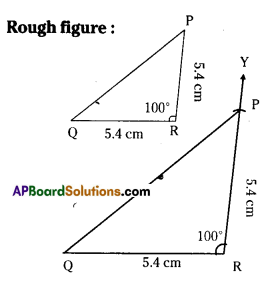
∠R= 100°,QR= RP = 5.4cm.
Step -1: Draw a rough sketch of a triangle and label it with the given measUrements.
Step -2: Draw a line segment QR of length 5.4 cm.
Step -3: Draw a ray \(\overrightarrow{\mathrm{RX}}\) making an angle 100° with QR.
Step -4: Draw an arc of radius 5.4 cm from R, which cuts \(\overrightarrow{\mathrm{RX}}\) at P.
Step -5: Join P, Q to get the required ΔPQR
![]()
Question 4.
Construct ΔTEN such that TE = 3 cm, ∠E = 90° and NE = 4 cm.
Solution:
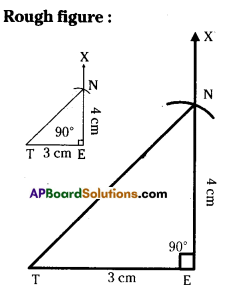
TE = 3cm, ∠E = 90°, NE = 4cm.
Step -1: Draw a rough sketch of the triangle and label it with the given measurements.
Step -2: Draw a line segment TE of length 3 cm.
Step -3: Draw a ray \(\overrightarrow{\mathrm{EX}}\) making an angle 90° with TE.
Step -4: Draw an arc of radius 4 cm from E, which cuts \(\overrightarrow{\mathrm{EX}}\) at N.
Step -5: Join N, T to get the required ΔTEN.
