AP State Syllabus 7th Class English Important Questions Unit 5
7th Class English Important Questions Unit 5
1. Read the following passage carefully.
In the evening, we boarded a ship for Port Blair, the capital of the Andaman and Nicobar Islands. The ship looked much bigger than our school building. It had four storeys. It set out after sounding a loud horn. People who had come to see off their friends and relatives cheered them up by waving their hands. My sister Amala and I too waved our hands while Mom and Dad smiled at us.
Now answer the following questions.
1) What is the capital of city of Andaman & Nicobar Islands?
2) Who were travelling to Andaman and Nicobar Islands?
3) What is the ship compared to?
4) Name two places where people come to see off their friends and relatives.
5) Why did the writer’s parents smile at him and Amala?
Answer:
1) Port Blair
2) The writer and his family.
3) A school building.
4) Airport, railway station, sea-port.
5) Because the writer and Amala enjoyed waving hands like other even though the people are unknown to them.

2. Read the following passage carefully.
Tall buildings, cell towers and factory chimneys began to vanish gradually. After a while, the twinkling lights of Chennai bade us farewell. Soon everything around us began to look dark and calm but inside the ship it was all bright and beautiful. When we closed the windows and doors of our cabin, we did not feel the movement of the ship.
On the second day, we came to know that we were in the middle of the sea. The weather was pleasant on the sea. The day was sunny and the sea was reflecting the clouds like a flat mirror. We saw Dolphins swimming along the ship. They sprang and dived again and again. It was quite amusing.
Now answer the following questions.
1) Where did the writer and his family board the ship?
2) How was it inside the ship even in the dark?
3) How was the weather in the sea?
4) Which sea animals are mentioned in the passage?
5) What was the amusing thing for the writer?
Answer:
1) The writer and his family boarded the ship at Chennai port.
2) Inside the ship it was all bright and beautiful.
3) The weather was pleasant on the sea.
4) Dolphins
5) The sprinihg and diving of Dolphins was amusing to the writer.
3. Read the following passage.
I was dUrious to know what other people were doing on the ship. So I went around. I saw some watching films and some others eating and drinking in the restaurants. A few were buying things in the fancy stores. I was surprised to see some in a saloon getting their hair cut.
The medical staff was busy treating the patients suffering mostly from sea-sickness. The sanitary workers were on their job of keeping the cabins, corridors and toilets neat and clean. The crew of the ship was very friendly and courteous. They gladly answered all my queries about the ship.
Now answer the following questions.
1) Who went around the ship?
2) Why did the speaker go round the ship?
3) What were the people doing on the ship?
4) How were the crew with the people on the ship?
5) What do we call the people who work on the ship?
Answer:
1) The writer
2) He was curious to know what qther people were doing on the ship.
3) Some were watching films, some were eating and drinking, some were buying things and others in the hair cutting saloon.
4) The crew of the ship was very friendly and courteous.
5) Crew

4. Read the following passage.
Dad said, “I know a little. There are about six hundred islands. They are located between India’s coast and Myanmar. Only 37 of them are inhabited. They have plant, animal and marine life in abundance.”
We learnt that the inhabitants of the islands were the aboriginal tribes. Some of them lived far away from the civilized society. Despite this, the islands today look like a miniature India. We saw people of different languages, cultures, and faiths living together happily.
We visited a famous national monument, the Cellular jail. We learnt that the Cellular jail was built by the British. It was nd longer a jail. It had been converted into a big hospital.
Now answer the following questions.
1) How many islands are there in the Andaman and Nicobar islands?
2) What is inhabitance?
3) How did the islands look like to the writer?
4) What is the famous monument in the islands?
5) What has the Cellular jail changed to?
Answer:
1) There are about six hundred islands.
2) The existence of plant, animal and marine life is called inhabitance.
3) The islands looked like a miniature India.
4) The Cellular jail
5) It was changed into a big hospital.
5. Read the following passage.
After a while, we reached an exciting place, the Mahatma Gandhi Marine National Park.
The park was spread over a wide area of 15 islands. Open creeks running through the park area were a special attraction. We watched coral reefs, fishes of different celours and sea turtles through glass-bottomed boats. For some time, we felt ourselves as a part of them. Amala and I cheered the fish and turtles.
We travelled by a ferry from Port Blair to a place called Havelock island. The ferries carry people, vehicles and goods. We enjoyed panipuri, samosas and gharam chai during the ferry journey.
Now answer the following questions.
1) What is the exciting place visited by the writer’s family?
2) What is the special attraction on the island?
3) Name some sea animals mentioned in the passage.
4) What is the means of transport to reach Havelock islands from Port Blair?
5) What is a ferry?
Answer:
1) Mahatma Gandhi Marine National Park
2) Open creeks running through the park area.
3) Fishes and turtles
4) Ferry
5) A ferry is a small boat to carry people, vehicles and goods.

6. Read the following passage.
A majestic lighthouse greeted us on our arrival at the Havelock Island. We felt as if the sandy beaches and greenish-blue sea were warmly welcoming us.
Some foreign tourists on the beaches were basking in the sun and enjoying themselves. We saw tourists enjoying swimming in the sea, and riding on elephants. Silky sands, foaming tides and cool breeze of the sea attracted us very much. We took lots of pictures of the beautiful scenery.
Now answer the following questions.
1) What looked very grand and royal in the Havelock Island?
2) What welcomed the tourists to the island?
3) What is the meaning of basking?
4) What was the most fun making and amusing activity for the tourists here?
5) The sea was attractive to the tourists. Why?
Answer:
1) Light house
2) The sandy beaches and greenish-blue sea
3) Drying up oneself in the sun.
4) Swimming in the sea and riding on elephants.
5) Because there was silky sand, foaming tides and cool breeze.
7. Read the following passage.
We visited the beach called Elephant beach. To our amazement, we saw some swimmers
diving into the sea from the motor boats. They were dressed in a different way. They put masks on their faces and carried air cylinders on their backs.
I asked Dad, “Why are the swimmers diving into the sea?”
Dad replied, “They want to watch the coral reefs and beautiful coloured fishes and sea turtles. They stay for a long time beneath the sea and swim along with them. lt is called Scuba diving.” The Scuba diving filled my heart with a spirit of adventure. I wished 1 could do it.
Now answer the following questions.
1) What is Scuba diving?
2) Why do swimmers dive into the sea?
3) Why do the swimmers carry air cylinders?
4) Name the place where the Scuba diving is done.
5) Can you name two adventurous acts?
Answer:
1) Diving deep into the sea and spending time watching the sea animals is called Scuba diving.
2) They want to watch the coral reefs and beautiful coloured fishes and sea turtles.
3) Because they stay for a long time under the sea and need air to breathe.
4) Elephant beach
5) Trekking, mountaineering, surfing on the sea.

B. Reading
1. Read the following lines.
I was sitting alone in my house,
Studying the structure of a mouse,
My exams were going on.
And science I hadn’t done.
Suddenly the lights went out,
Then I heard a loud burst,
Someone was there, outside,
I went out to look, full of fright.
Now answer the following questions
1) Who was ‘I’ in the poem?
2) What was the speaker doing?
3) What was the subject the speaker was not ready with?
4) Why did the speaker feel someone was outside?
5) How do you feel when you were alone at home?
Answer:
1) The boy/ the poet
2) He was preparing for science exam.
3) Science
4) Because he heard a loud burst.
5) A little scared if it is night.
2. Read the following stanza.
I saw a huge rocket,
And an astronaut in white,
He invited me on a flight to the moon,
We reached there by afternoon.
We jumped around
As we couldn’t walk on the ground.
Now answer the following questions.
1) Do you think the child really went on the moon?
2) Who is an astronaut?
3) Why couldn’t the speaker and the astronaut walk on the ground?
4) How did the speaker feel on the moon?
5) How would you feel if you were invited on the moon?
Answer:
1) No, it was his dream.
2) A person who studies about other planets/travels in space.
3) Because there was no air in the space.
4) It was exciting to the speaker to spend time on the moon.
5) I would feel very happy and delightful.

3. Read the following stanza.
We jumped around
As we couldn’t walk on the ground.
It was a lot of fun,
I reached home before the setting sun.
My science test went very well,
But no one knows the secret,
Which even now inside me dwells.
Now answer the following questions.
1) Who does ‘we’ refer to?
2) Where were they?
3) How did the speaker reach home?
4) What was the secret about the speaker?
5) If you were given a chance, which planet do you prefer to visit?
Answer:
1) The poet and the astronaut
2) They were on the moon.
3) By rocket
4) The secret was that the poet spent his time in the space. The speaker learnt everything by self experience.
5) Mars
C. Reading
1. Read the following passage.
I bought a substantial stock of goods to trade, and sailed on a ship with a number of my merchant friends. We placed ourselves in the care of Allah and set off. Soon we reached an island.
We decided to go ashore. My friends went to gather fruits and flowers, but I took my food packet to a place in the shade. I had a good meal and lay down to sleep under the trees. I don’t know how long I slept, but when I awoke and looked out to sea, the ship had gone. I was all alone. Not knowing what to do, I climbed up to the top of a tall tree and looked over the island on all sides. In the distance I could see something white, and decided to find out what it was.
Now answer the following questions.
1) Who does ‘I’ refer to?
2) Why do you think the speaker bought the stock of goods?
3) Who accompanied the speaker?
4) What did the speaker realise after he woke up?
5) What would you do if you were left alone in a place?
Answer:
1) ‘I’ refers to Sindbad.
2) The speaker bought the goods to trade.
3) His friends
4) The speaker realised that the ship had gone leaving him alone on the island.
5) I would search for a companion.

2. Read the following passage.
Suddenly, the sky above me became dark, as if a huge cloud was covering it. Looking up,
I saw that the darkness was caused by the shadow of a huge bird that was flying towards me.
I had often heard sailors talk of a great and wonderful bird, called a ‘roc’. This must be a roc,
1 thought, and this huge ball must be its egg!
The bird came nearer and sat on its egg. I soon crept close to the egg. Near me was one of the bird’s legs, which was as big as a tree. I decided to tie myself to the leg of this bird with my turban so that when it flew away from the island, it would carry me with it.
Now answer the following questions.
1) What made the sky dark?
2) How is the bird described?
3) What is the egg of the bird compared with?
4) How big was the bird’s leg?
5) What was the plan of escape made by the speaker?
Answer:
1) It was the shadow of a huge bird that came between the speaker and the sky.
2) Huge, great and wonderful.
3) Huge ball
4) The leg was as big as a tree.
5) The speaker tied himself to the leg of the bird with his turban.
3. Read the following passage.
At day break, the bird flew up so high that 1 was carried out of sight of the island. Then it came down again so fast that I lost my senses. When I found myself on the ground, I quickly untied the turban. The bird caught up a snake and flew away.
This time I found myself surrounded on all sides by immense mountains that seemed to reach above the clouds. The sides of the valley looked so steep that there was no possibility of climbing them. When I began to look around the valley, I found that there were large diamonds lying on the ground.
Now answer the following questions.
1) What happened to the speaker when the bird landed very fast?
2) Where did the bird leave the speaker?
3} How were the mountains?
4) Have you ever climbed mountains? What is mountain climbing called?
5} What did the speaker find in the valley?
Answer:
1) The speaker lost his senses.
2) In a valley
3) The mountains were immense/very big in size.
4) No, I did not climb a mountain. Mountain climbing is called Alpinism or Mountaineering.
5) Huge serpents
4. Read the following passage.
I was excited to find such riches lying around me. Then I saw something else that made
roe very frightened. All around the valley there were huge serpents, some of them big enough to even eat an elephant! These came out of their holes at nightfall. During the day, I suppose, they hid themselves from the rocs.
I found a small cave where I decided to spend the night. At the entrance I put a large stone to protect myself from the serpents, but the noise of their hissing outside made sleep impossible.
Now answer the following questions.
T) How would you feel if you find diamonds?
2) What is the valley inhabited with?
3) How did the speaker try to protect himself?
4) What made the speaker unable to sleep?
5) Did you ever face a serpent? What did you do to escape?
Answer:
1) Very excited
2) Huge serpents
3) The speaker protected himself by taking shelter in the rocks in the night.
4) The hissing noise of the serpents.
5) No. I never faced a serpent.

5. Read the following passage.
I had heard stories in the past about this valley of diamonds, but had not believed them. Now I saw with my own eyes what the local merchants did to obtain the jewels; they used huge eagles to carry up the diamonds for them!
When the eagles have young ones in their nests among the rocks, they fly down into the valley to get food for them. So, the merchants would throw down large pieces of raw meat; the diamonds stick to the meat, and in this way get carried to the eagles nests. Each merchant has his own nest, and considers its jewels his. The idea came to me that I too could use these eagles I myself could be lifted up from this deep valley, and thus escape from it! The eagles were so big and strong that my weight would seem little.
Now answer the following questions.
1) What did the merchants do to obtain jewels?
2) Why did the eagle fly down into the rocks?
3) What happens to the diamonds when the merchants throw meat into the valley?
4) How did the speaker try to escape from the valley?
5) What would you do with the diamonds if you get them?
Answer:
1) The merchants threw meat to make the diamonds stick to them. When the eagles pick them up as food, they separate the diamonds from the meat.
2) To pick the meat.
3) The diamonds stick to the meat.
4) The speaker tied a large piece of meat to his back and laid on the ground enabling the eagle to carry him.
5) I would keep some for my living and help the poor with others.
6. Read the following passage.
First, I collected a number of large diamonds. These I put in my wallet and tied the wallet
to my waist. Next, I tied one of the large pieces of meat to the middle of my back with my turban. I then lay down with my face to the ground, and waited there. There was the sound of huge wings around me. Then I felt myself lifted up and carried to the top of the rocky walls of the valley.
Soon I was in one of the nests. The merchants were surprised to see me there, and I when they heard my story, they helped me to find a ship to go home. When I got back to Baghdad.
I was a very wealthy man. I gave large amounts of money to the poor and lived peacefully in my own home.
Now answer the following questions.
1) Why did the speaker tie large pieces of meat to his back?
2) Who carried the speaker to the top of the valley?
3) Who helped the speaker reach home?
4) What good’work did the speaker do after reaching home?
5) What do you call the incidents that took place with the speaker?
Answer:
1) To attract the eagles
2) The eagle
3) The merchants
4) He gave large amounts of money to the poor.
5) Adventures

Unseen Comprehension
1. Read the following passage carefully.
From the architectural and cultural point of view, India is one of the most famous countries all over the world. Here is the variety in clothing, food, culture, tradition, language, living status etc. because of the presence of many religions all over the country. So, people become more interested to travel India more than once in their life time. India is the right place for the historical and peaceful scenery visits. India is most populated and multicultural country however
famous for unity in diversity. India is the motherland Of the worldwide famous legends such as Mahatma Gandhi, Gautama Buddha, Rani Lakshmi Bai, Ratan Tata and so many. India is the country having well-developed cities, heritages, monuments and other sight seeings such as Taj Mahal, Great Indian Himalayas, Bengal Tiger, etc. which are considered as the icons of India tourism.
Now answer the following questions
1) What made India one of the most famous country in the world?
Answer:
India is famous for its architecture and culture.
2) India has people following many religions. What is the effect of this feature?
Answer:
There will be variety of traditions, culture, food, clothing, languages, etc.
Choose the correct answer from the choices given.
3) Foreigners visit India more than once because
a) there are many forests.
b) there are many cities.
c) people are very beautiful.
d) the country has a great history and scenic beauty.
Answer:
d) the country has a great history and scenic beauty.
4) What do we call ‘Mahatma Gandhi’ nationwide ?
a) Gandhiji
b) Bapu
c) Mahan
d) Guruji
Answer:
b) Bapu
5) Where is Taj Mahal?
a) In Taj
b) In Telangana
c) In Delhi
d) In Agra
Answer:
d) In Agra

2. Read the following passage carefully.
A visit to an exhibition is a novel experience. An exhibition which I visited recently was very interesting. It was one of the largest exhibitions ever held. Being a Sunday there were many visitors that made it difficult to walk.
Men, women and children in their colourful and best dresses were there. At the booking counter there were long quees. I bought tickets and entered the exhibition ground. Our parents and I enjoyed the exhibition for a long time. The grounds were tastefully decorated. There were stalls and pavilion of ministries, companies and states.
There were hundreds of exhibits for the domestic use.. By the time we came out of the German pavilion, we were very tired. We went to a coffee-shop and had hot coffee. My mother bought a shawl. There was a village complex with many village singers, jugglers and folk artists. The puppet show was very amusing.
Now answer the following questions
1) What is necessary to visit the exhibition?
Answer:
An entrance ticket
2) Who is a juggler?
Answer:
One who does magic is a juggler.
Choose the correct answer:
3) When is it difficult to go around in exhibition? ( )
a) Sunday
b) Tuesday
c) Working day
d) In the morning
Answer:
a) Sunday
4) What was very entertaining for the author? ( )
a) Stalls
b) Coffee shop
c) Puppet show
d) Exhibition
Answer:
c) Puppet show
5) What did the writer’s family do when they were tired? ( )
a) They sat down and released.
b) They went to a coffee shop and had coffee.
c) They bought toys and shawl.
d) They went home.
Answer:
b) They went to a coffee shop and had coffee.
3. Read the following passage carefully.
Sally jumped up as soon as she saw the surgeon come out of the operating room. She said: “How is my little boy? Is he going to be all right? When can I see him?” The surgeon said, “I’m sorry. We did all we could, but your boy didn’t make it”. Sally said, “Why do little children get cancer? Doesn’t God care any more ? Where were you, God, when my son needed you?”
The surgeon asked, “would you like some time alone with your son? One of the nurses will be out in a few minutes, before he’s transported to the university”.
Sally asked the nurse to stay with her while she said goodbye to son. She ran her fingers through his curly hair. “Would you like a lock of his hair?” the nurse said. She cut a lock of the boy’s hair and gave it to Sally in a plastic bag. Sally said, “It was Jimmy’s idea to donate his body to the university for study. He said it might help somebody else. “She continued,” My Jimmy had a heart of gold. Always thinking of some one else. Always wanting to help others if he could”.
Now answer the following questions.
1) Who was admitted in the hospital?
Answer:
Sally’s son
2) What was the boy suffering from?
Answer:
Cancer
Choose the correct answer:
3) Where will the boy be taken after the surgery?
a) to his home
b) to hospital
c) to university
d) to a clinic
Answer:
c) to university
4) What did the nurse offer sally as a token of memory?
a) a gold win
b) a big chest of clothes
c) the boy’s clothes
d) a lock of hair of the boy
Answer:
d) a lock of hair of the boy
5) Why was the boy taken to the university?
a) to be operated
b) to get good treatment
c) to be helpful for the study of others
d) to help the doctors
Answer:
c) to be helpful for the study of others

4. Read the following passage carefully.
Gardening! It is a hard work. It is even a dirty work. You have to dig up the hard earth and make its heart soft. Not only this. You have to plan it well. You have to lay out beds for different kinds of plants. They require great care. They must get food and water in time. All this requires hard work and it fills your body with dirt and sweat.
A Gardener is like a mother to the garden. No, good mother leaves her children to a nurse. So as a gardener your garden requires food and water, love and affection. A plant is also a living being and has feelings like a human or an animals. The beauty of flowers, the medicinal value of some plants, the utility of the branches alre all the benefits of possessing a garden.
The hobby of gardening is good for health, fitness and recreation. It involves physical activities in open air. The study of plant life is very interesting.
Now answer the following questions.
1) Why should the hard earth be made soft?
Answer:
To sow the seeds or plant new saplings.
2) Why is gardening a hard work?
Answer:
Because the soil has to be dug, lay out beds, plants must be watered regularly, etc.
Choose the correct answer:
3) Who is the mother of the garden? ( )
a) you
b) plants
c) gardener
d) people
Answer:
c) gardener
4) Who has feelings of pain, love, affection, etc.? ( )
a) gardener
b) plants
c) animals
d) all the three
Answer:
d) all the three
5) What is the study of plant life called? ( )
a) gardening
b) biology
c) anatomy
d) plantology
Answer:
b) biology
5. Read the following passage carefully.
Mother Teresa is also known as ‘Blessed Teresa of Calcutta”. Her earlier name was ‘Anjeze Gonxhe Bojaxhier” She was born on 26th August, 1910 at the then Yugoslavia. She came to India in 1929. Mother Teresa was Roman Catholic nun moved to Calcutta’s slum “to serve God among the poorest of the poor”.
In 1950, she established the Missionaries of Charity to help the poor, helpless, disabled, diseased refugees and lepers. Today, the missionaries of charity are in more than 100 countries.
She was awarded the title of “Padma Shri” in 1962. She received the Nobel Peace Prize in 1979. Later in 1980, she received conferred the title of ‘Bharat Ratna”, the highest civilian award in India. She was the first citizen of India to win Nobel Peace Prize.
Now answer the following questions.
1) What is the other name for Mother Teresa?
Answer:
‘Blessed Teresa of Calcutta’
2) What was the birth place of Teresa?
Answer:
Yugoslavia
Choose the correct answer from the choices given.
3) When did Mother Teresa found the Missionaries of Charity?
a) 1980
b) 1929
c) 1950
d) 1919
Answer:
d) 1919
4) What was the award received by Teresa in 1979?
a) Nobel Prize
b) Padma Shri
c) Blessed Teresa
d) Bharat Ratna
Answer:
c) Blessed Teresa
5) Where did Mother Teresa find God?
a) in the city of Calcutta
b) in the school of charity
c) in Yugoslavia
d) in the poorest of the poor
Answer:
a) in the city of Calcutta

6. Read the following passage.
There was a Guru who had mastered the Scriptures. One day when he was teaching the] Vedas to his disciples, a cat started moving around. This did not disturb the Guru, but was a distraction to some of his disciples. So the Guru instructed his disciples to get hold of the cat and tie it to pillar. As the nuisance recurred on the following days, the cat was regularly tethered to the pillar before the Guru began his teaching.
Some years later the Guru died. One of his disciples became the new head. The practice of tethering the cat to the pillar continued. After a few months the cat died. When the Guru began his teaching the next day he noticed that the cat was missing. He said, “Don’t you know that a cat must be tied to the pillar during my teaching ? That is our tradition. Go and find a cat”. The disciples immediately obeyed the order. Blindly following traditions, thus, is foolish and serves no purpose.
Now, answer the following questions.
1) Why were the disciples distracted?
Answer:
A cat’s moving around distracted the disciples.
2) What was done to prevent the cat from roaming about?
Answer:
The cat was tied to the pillar.
Choose the correct answer from the choices given below.
3) Who became the new head? ( )
a) One of the disciples of the Guru
b) The cat
c) All the disciples
Answer:
a) One of the disciples of the Guru
4) What practice continued after the new Guru took charge? ( )
a) Keeping the cat near the Guru
b) Tethering the cat to the pillar
c) Making it go round the pillar
Answer:
b) Tethering the cat to the pillar
5) Choose the correct statement from the following. ( )
a) The new Guru was foolish because he was blindly following a practice.
b) The new Guru was foolish because he was fond of cats.
c) The new Guru was foolish because he disliked traditions.
Answer:
a) The new Guru was foolish because he was blindly following a practice.
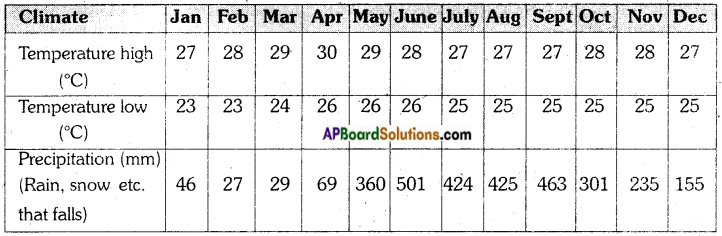
1. This table shows the climate of Port Blair from January to December 2015
Now answer the following questions.
1) What is the highest temperature recorded in 2015?
Answer:
April
2) Which months experience the lowest temperature?
Answer:
January and February
Choose the correct answer from the choices given.
3) In which month is the precipitation high? ( )
a) March
b) July
c) June
d) December
Answer:
c) June
4) Which months have a stable low temperature? ( )
a) Jan-May
b) May-Sept
c) Oct-Dec
d) July-Dee
Answer:
d) July-Dee
5) According to the table, which of the following statement proves to be true? ( )
a) The precipitation has been high in the middle of the year.
b) Port Blair is a beautiful city.
c) The minimum temperature has been decreasing from January to December.
Answer:
a) The precipitation has been high in the middle of the year.

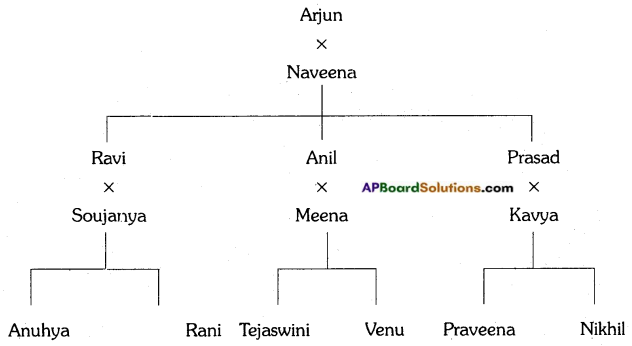
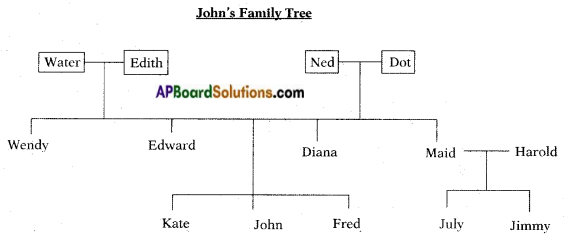
2. Given below is John’s family tree. Study and answer the questions.
Now answer the following questions.
1) Who are John’s parents?
Answer:
Edward and Diana
2) Who is the sibling of Diana?
Answer:
Maid
Choose the correct answer from the choices given.
3) Wendy and Edward are ( )
a) cousins
b) brother and sister
c) daughters
d) parents
Answer:
b) brother and sister
4) Who did Maid-marry? ( )
a) Edward
b) Fred
c) Harold
d) Jimmy
Answer:
c) Harold
5) How many people exist in 3rd generation of the family chart? ( )
a) 5 members
b) 10 members
c) 6 members
d) 4 members
Answer:
a) 5 members
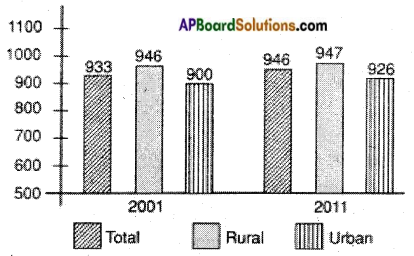
3. The bar graph below shows the Sex ratio of females per 1000 males. Study the graph and answer the questions.
Now answer the following questions.
1) What is the Rural female population during 2001?
Answer:
946 females
2) What is the difference in the population from 2001 to 2011?
Answer:
The population has increased in 10 years of time.
Choose the correct answer from the choices given.
3) How many females are existing in urban areas in 2011? ( )
a) 947
b) 900
c) 926
d) 947
Answer:
c) 926
4) The ratio of male : female in 2011 in rural area is ( )
a) 1000: 933
b) 1000 : 947
c) 900 : 1000
d) 946 : 1000
Answer:
b) 1000 : 947
5) Which of the following statement is true according to the graph representation? ( )
a) In 2011, the urban female population is lesser than the total population.
b) The female population decreased in 2011 when compared to 2001.
c) The male and female population is same in 2001 in rural areas.
Answer:
a) In 2011, the urban female population is lesser than the total population.

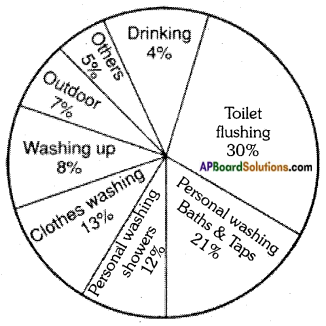
4. The pie chart below shows the usage of water for domestic purposes. Study it and answer the questions.
Now answer the following questions.
1) For which purpose is water mostly used on domestic front?
Answer:
Toilet flushing
2) What are the different kinds of washing mentioned in the pie chart?
Answer:
Washing up, clothes washing, personal washing showers, personal washing baths and taps
Choose the correct answer from the choices given.
3) Water used for is very less. ( )
a) personal washing showers
b) toilet flushing
c) drinking
d) washing hands
Answer:
c) drinking
4) What is the percentage of water used for outdoor purposes? ( )
a) 12%
b) 7%
c) 21%
d) 5%
Answer:
b) 7%
5) Pick out the true statement with reference to the details in the pie chart. ( )
a) Water is best utilized for clothes washing.
b) Consumption of water for various washing purposes can be minimised/reduced.
c) Water is the main source for keeping ourselves and surroundings clean.
Answer:
c) Water is the main source for keeping ourselves and surroundings clean.
5. Study the following tree diagram carefully.
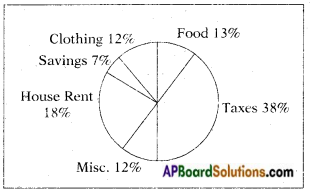
Distribution of annual income of Ramesh on savings and expenditure
Now, answer the following questions.
1) What does the above pie chart describe?
Answer:
Distribution of annual income of Ramesh on savings and expenditure
2) What is the second highest expenditure of Ramesh?
Answer:
House rent
Choose the correct answer from the choices given below.
3) Ramesh spends the most on ( )
a) taxes
b) clothes
c) miscellaneous
Answer:
a) taxes
4) Ramesh spends the least on ( )
a) taxes
b) clothing
c) food
Answer:
b) clothing
5) Which of the following statements is true with reference to the information given above? ( )
a) Ramesh spends equally on clothing and miscellaneous items.
b) Ramesh does not have any savings.
c) Ramesh spends more on clothing than food.
Answer:
a) Ramesh spends equally on clothing and miscellaneous items.

Section – B: Creative Writing
1. In the lesson A Trip to Andaman’, the writer’s Dad made it possible for the family on a trip to Andaman during summer vacation. Write a conversation between writer and his dad about planning during summer holidays.
Answer:
Writer: Hi Dad, a good news. Our summer vacation is from tomorrow.
Dad: Is it? Very good. I shall take leave from the office. Let’s plan to go somewhere.
Writer: That’s exciting! Where shall we go?
Dad: I have already thought about it. We shall plan for Andaman and Nicobar islands.
Writer: Are we flying?
Dad: No. let us make a trip by ship.
Writer: Wow, that’s wonderful.
Dad: Let us inform your mother. She will pack all the necessary things.
Writer: Is there anything specific to carry?
Dad: Nothing. But let us carry our sweaters and shawls.
Writer: Ok Dad. I shall help Mom do the arrangements.
Dad: Fine. Let us go and tell your mother and your sister Amala.
Writer : Yes.
2. Describe a journey you made with your family.
Answer:
Recently we planned a tour to Araku Valley. Dad said it’s a very pleasant and cool hill station that can be visited in summer. Charan and I were so excited and told our friends about our trip to Araku. Mom also said its a worthy sight seeing place.
We started early in the morning of Monday by a train to Vishakhapatnam. I enjoyed the climate and scenic beauty sitting by the window. Mom made some snacks and lunch for us to enjoy during the journey. We reached Vishakhapatnam in the afternoon. We took rest in a hotel and went to see R.K. Beach in the evening. First time, to go near the heavy waters scared me a lot. But my father held our hands and gave the courage to go near the waters. We enjoyed a lot with the on and off movements of tides.
We took rest for the night and started for Araku early in the morning by train. The journey was pleasant and exciting as we passed through forests and tunnels. Children in the train shouted with joy. We reached Araku, hired a room and got fresh. We hired a taxi to see some old temples. Borra caves, tea and coffee plantations and beautiful gardens. We enjoyed the trip. The garden was beautiful with flower beds, bushes and decorated trees.
The trip was a memorable experience in my life.
3. There was discipline maintained by the crew on the ship. Write a diary entry of the writer about his feelings on the behaviour of the crew on the ship.
Answer:
12th June, Tuesday.
We returned home yesterday after a joyful trip to Andaman and Nicobar islands. When Dad said we are going by ship 1 was afraid of the sea waters and journey by ship. But all my fears vanished when I saw the hospitality of the crew on the ship.
The crew on the ship took utmost care in making arrangements for the travellers. They wandered from one place to another giving right directions. They showed a lot of patience to explain the tourists about the utilization of facilities on the ship. They smiled at everyone and bore the naughty behaviour of children like us. They served at every door of the room and were very friendly and courteous. We liked them and became friends very soon. The crew < never wasted their time. They even worked in the night when everyone slept. The journey was comfortable and enjoyable because of them.
We thanked the crew before we left the port. They smiled and simply bowed in respect.

4. The Inhabitants of the Islands look like a miniature India because there are different languages, cultures and faiths living together. This is called Unity In Diversity. We find the same culture in India. Write a speech on Unity ¡n Diversity that
prevails in India.
Answer:
‘Unity in Diversity’
Respected teachers and my dear friends,
… India is a country that is well known for its ‘Unity in Diversity’. So I feel honoured and proud to speak before you on this remarkable feature of India.
Unity in diversity means oneness In the varieties. India is a country where it is very clear to see this concept because people of many religion, race, culture and traditions live together without affecting each others feelings and believes to their religion. Unity in Diversity focuses in the existence of oneness even after lot of differences of cultural, social, physical, linguistic religions, political, ideological, psychological, etc. More number of differences make more complex unity. People in India are united in spite of the much diversity of races, religions, castes, sub-castes, communities, languages and dialects. People in India are highly spiritual and God fearing in nature so they give respect to everyone’s religion.
Humanity and likelihood of people help them to maintain the policy of Unity in Diversity. We are proud to be Indians”
5. Describe a park or a zoo you visited.
Answer:
We have a small park in front of our house where we go to play every evening. Ours is a residential area with many houses in rows, a few flats and some shopping complexes. Our house in the centre of the street. There is a small park in front of our house. There is a gardener who looks after the park. The park has well cut bushes all around it and trees here and there giving shade to the visitors.
The park is open from 4 p.m. every day. On Sunday, it is open since 6 a.m. in the morning for walkers and children. We go to park every day after school to play and have fun. It is a dwelling place for elders too. Some teenagers come there to read a book or call a friend and have relaxed chat. I love the park. Sometimes I take my comics and drawing books to read and paint.
Every Sunday the park looks like a picnic spot. We have play things like turnstile, merry go round, slide, bells and dens and hiding places to play hide and seek. There are also big structures of animals and people. We can climb them and sit there. y
The park is a place of entertainment, recreation and fun making activities.

6. Your father is interested to join you in swimming, but you are afraid of water.
Write a possible conversation where your father tries to convince you to join swimming.
Answer:
Father: Bunny. Here is an exciting news for you!
Bunny: What is it, Dad?
Father: I would like to join you in swimming classes this summer.
Bunny: Oh, no Dad. I’m afraid of water.
Father: Don’t be silly. You’re a brave boy. Swimming is a very good exercise.
Bunny: But I can’t swim. I may drown in the water.
Father: No boy. There will be a trainer to teach you swimming. Moreover the water is only 5 feet deep.
Bunny: Is it so easy?
Father: The coach will make it easy and comfortable. First you’ll practise with the support of a ring and slowly individually.
Bunny: Are you also accompanying me?
Father: Yes, of course.
Bunny: Then its OK. I shall join the classes from tomorrow.
1. Here is the profie of a great swimmer Virdhawal Khade. Write a biosketch of the great swimmer Virdhawal Khade.
Answer:
Full Name: Virdhawal Vikram Khade
Nickname: Veer
Nationality: Indian
Born: August 29, 1991 (Age 24)
Kolhapur, Maharashtra
Height: 6ft 3″
Weight: 83 kg
Sport: Swimming
Strokes: Free style, Butterfly
Medal record: Swimming, Asian games
Answer:
Biographical Sketch:
Virudhawal Vikram Khade, shortly known as ‘Veer’ is an Indian swimmer, who earned fame and name in swimming world. He was born on 29th August, 1991 in Kolhapur, Maharashtra. He is 24 years old. He was 6 feet 3 inches tall and weighs about 83 kgs.
Vikram Khade was famous in swimming free style and Butterfly strokes in swimming. He participated in Asian games and won medals for the country. We should encourage people with such talent because they are the pride of the nation.
2. Two boys of 13 years went swimming into the nearby river after school hours. They were drowned in the water as they went very far into water. Write a news report on this incident.
Answer:
TWO BOYS DIED IN WATER: PARENTS IN DEEP SORROW
13th September, 20xx, Vijayawada: Two children of 10 years and 11 years of the nearby area at Yanamalakuduru, Vijayawada went into the waters for bath and swimming and lost their lives; reporters said.
Veeraswamy (10 years) and Adidas (11 years) went into the water making fun and swimming after the school hours on Wednesday. While playing, they did not observe going far into the water. Suddenly the speed flowing water pulled swamy. He lost his balance and went along with the water. Adidas who tried to help him also was dragged away by the water, flow. Both of them drowned in the water.
The dead bodies were recovered by the search team. The parents sorrow knew no bounds. The police were reported and they are investigating the case. The local people demanded for some security check in such places where there is hidden danger.
News Reporter The Hindu.

3. Your elder sister is going to be married. You have to attend the marriage function. You have to spend 4 days at home. You cannot attend school these days. Now, write a letter to your class teacher applying for leave of absence for four days.
Answer:
Tenali.
10-3-xx.
To
The Class Teacher,
7th Class, A/S,
Municipal Boys High School,
Tenali.
Respected Sir,
My elder sister’s marriage is going to be celebrated on 20th of this month at Tirupathi. I have to help my parents in making arrangements and I have to attend the marriage function. I have to spend for four days. I cannot attend school these days.
Hence I request you to sanction leave for four days from 18.3.xx to 21.3.xx.
Thanking you sir,
Yours obediently,
x x x x x
Roll No: 23,
VII Class, A/S,
Municipal Boys School,
Tenali.
Vocabulary
1. Read the following paragraph and write the synonyms of the underlined words choosing the words from the words given in the box.
1.

After lunch, we hired (a) a taxi for the port. In the evening, we boarded (b) a ship for Port Blair.
2.

It set out (a) after sounding a loud horn. People who had come to see off their friends and relatives cheered (b) them up by waving their hands
3.

Tall buildings, cell towers and factory chimneys began to vanish (a) gradually. After a while, the twinkling lights of Chennai bade us farewell (b).
4.

The Dolphins sprang and dived (a) again and again. It was quite amusing (b).
5.

The crew of the ship was very friendly and courteous (a). They gladly answered all my queries (b) about the ship.
6.

Early in the morning, Mom woke us up to show us the magnificent (a) spectacle of the dawn (b) at the sea.
7.

Only 37 of them are inhabited (a). They have plant, animal and marine life in abundance (b).
8.

Despite this, the islands today look like a miniature (a) India. We saw people of different languages, cultures, and faiths (b) living together happily.
9.

Open creeks (a) running through the park area were a special attraction. We watched coral reefs (b), fishes of different colours and sea turtles through glass-bottom boats.
10.

To our amazement (a), we saw some swimmers diving into the sea from the motor boats. They were dressed in a different way. They put masks (b) on their faces.
11.

We tasted delicious (a) Tandoori fish and other sea foods on the islands. My mouth still waters when I remember those moments. I cherish (b) the memory of the great fun we had.
Answers:
1. a) taken for rent b) to enter, get into
2. a) started b) greeted
3. a) disappear b) good bye
4. a) jump into water from a height b) entertaining
5. a) kind and helpful b) questions
6. a) wonderful b) rising of sun
7. a) living area b) sufficient
8. a) small b) religious belief
9. a) streams b)rocks
10. a) surprise b) a cover to the face
11. a) tasty b) enjoy

2. Write the opposite words to the underlined words in the given paragraph.
1. After lunch, we hired (a) a taxi for the port. In the evening, we boarded (b) a ship for Port Blair.
2. The ship looked much bigger (a) then our school building. It had four storeys. It set out after sounding a loud (b) horn.
3. Tall (a) buildings, cell towers and factory chimneys began to vanish gradually (b).
Soon, everything around us began to look dark (a) and calm (b) but inside the ship it was bright and beautiful.
5. The weather was pleasant (a) on the sea. We saw Dolphins swimming, springing and diving along the ship. It was quite amusing (b).
6. I was curious (a) to know what other people were doing on the ship. So I went around. A few were buying (b) things in the family stores.
7. The crew of the ship were friendly and courteous (a). They gladly (b) answered all my queries about the ship.
8. After a while, we reached an exciting (a) place, the Mahatma Gandhi Marine National Park. The park was spread over a wide (b) are of 15 islands.
9. A majestic lighthouse greeted us on our arrival (a) at the Havelock island. We felt as if the sandy beaches and greenish-blue sea were warmly (b) welcoming us.
10. In the evening (a) we boarded the ship for Port Blair, the capital of the Andaman and Nicobar Islands. The ship looked much bigger (b) than our school building.
Answer:
1. a) owned b) alighted
2. a) smaller b) soft
3. a) short b) suddenly
4. a) bright b) noisy
5. a) unpleasant b) boring
6. a) reluctant b) selling
7. a) rude b) sadly
8. a) boring b) narrow
9. a) departure b) harshly
10. a) morning b) smaller
3. Fill in the blanks with the right form of words given in brackets.
1. Soon after the______ (a) (examines/examinations) were over, Mom made ______ (b) (preparations/prepares) for the trip,.
2. Soon everything around us began to look dark and calm but inside the ship it was all bright and ______ (a) (beauty/beautiful). When we closed the windows and doors of our cabin, we did not feel the _______(b) (movement/move) of the ship.
3. The medical staff were busy ________ (a) (treating/treat) the patients suffering mostly from sea ________ (b) (sick/sickness).
4. The crew of the ship were very _______ (a) (friend/friendly) and ________ (b) (courteous/courtesy).
5. Only 37 of them are __________ (a) (inhabitants/inhabited). They have plant, animal and marine life in ________. (b) (abundant/abundance).
6. Open creeks ___________ (a) (mn/running) through the park area wire a special __________ (b) (attraction/attract).
7. A majestic lighthouse greeted us on our ___________ (a) (arrive/arrival) at the Havelock Island. We felt as if the sandy beaches and greenish – blue sea were __________ (b) (warm/warmly) weLcoming us.
8. To our __________ (a) (amaze/amazement), we saw some swimmers diving into the sea from the motor boats. They were dressed in a __________ (b) (different/difference) way.
9. We saw people of___________ (a) (difference/different) languageš, cultures and faiths living together happily. We visited a famous (b) (national/nation) monument.
Answer:
1. a) examinations b) reparations
2. a) beautiful b) movement
3. a) treating b) sickness
4. a) friendly b) courteous
5. a) inhabited b) abundance
6. a) running b) attraction
7. a) arrival b) warmly
8. a) amazement b) different
9. a) different b) national

a) Complete the following words using ai, ea, ee, ei, eo, ie, oa, oo, ou, ui.
1. The ship looked much bigger than our (a) sch _ _ l (b) b _ _ lding.
2. (a) P _ _ ple came to see off their (b) fr _ _ nds and relatives.
3. The day was sunny and the (a) s _ _ was reflecting the (b) cl _ _ ds like a flat mirror.
4. I was surprised to see some in (a) sal _ _ n getting their (b) h _ _ r cut.
5. The medical staff was busy (a) tr _ _ ting the (b) pat _ _ nts suffering mostly from sea-sickness. .
6. The crew of the ship was very (a) fr _ _ ndly and (b) court _ _ us.
7. We watched coral (a) r _ _ fs, fishes arid sea turtles through glass-bottomed (b) b _ _ ts.
8. We felt as if the sandy (a) b _ _ ches and (b) gr _ _ nish blue sea were warmly welcoming us.
9. Some (a) for _ _ gn (b) t _ _ rists on the beaches were basking in the sun.
10. We tasted (a) delici _ _ s Tandoori fish and other (b) s _ _ foods on the islands.
11. After a while, we (a) r _ _ ched an exciting place, the Mahatma Gandhi Marine National park. The park was spread over a wide area of 15 islands. Open creeks running through the park area were a (b) spec _ _ l attraction.
Answer:
1. a) school b) building
2. a) People b) friends
3. a) sea b) clouds
4. a) saloon b) hair
5. a) treating b) patients
6. a) friendly b) courteous
7. a) reefs b) boats
8. a) beaches b) greenish
9. a) foreign b) tourists
10. a) delicious b) seafoods
11. a) reached b) special
b) Complete the words with the correct suffixes given in brackets.
1) The day was (a) sun ____ (y/ny) and the sea was (b) reflec (ting/tting) the clouds like a flat mirror.
2) The (a) medi ____ (cal/cel) staff was busy treating the patients (b) suffer ____ (ing/ring) mostly from sea-sickness.
3) The crew of the ship was very (a) friend ____ (ily/ly) and (b) courte ____ (ous/aus).
4) We learnt that the (a) inhabit ____ (ents/ants) of the islands were the (b) aborigin ____ (el/al) tribes.
5) We visited a (a) fam ____ (ous/aus) national (b) monu ____ (ment/ mant).
6) Open creeks (a) run ____ (ing/ning) through park area were a special (b) attrac____(ssion/tion).
7) We felt as if the sandy beaches and (a) green ____ (ich/ish) blue sea were warmly (b) welcom ____ (ing/eing) us.
8) To our (a) amaze____ (mant/ment), we saw some (b) swim ____ (mers/mars) diving into the sea from the motor boats.
9) A (a) majest ____ (ick/ic) lighthouse greeted uson our (b) arri ____ (val/vel) at the Havelock Island.
10) a) It was quite amus ____ (eing/ing).
b) They have plant. animal and marine life in aban____ (dance/dence).
Answer:
1. a) sunny b) reflection
2. a) medical b) suffering
3. a) friendly b) courteous
4. a) inhabitants b) aboriginal
5. a) famous b) monument
6. a) running b) attraction.
7. a) greenish b) welcoming
8. a) amazement b) swimmers
9. a) majestic b) arrival
10. a) amusing b abundance

c) Find the wrongly spelt word and write the correct spelling.
1. beach; cureas; majestic; beneath
2. enjoying; adventure; riding; costline
3. masks; jolyride; remember; payment
4. borded; chimneys; movement; swimming
5. medical; suffer; coridors; beautiful
Answer:
1) curious
2) coastline
3) jollyride
4) boarded
5) corridors
Put under correct headings.
A.

Answer:

B.

Answer:

C.

Answer:
A) Fill in the blanks with appropriate forms of words given in the brackets.
1. The gardener ___________ the plants every day. The plants grew well with the _________ (water).
2. Arjuna _________ an arrow at the bird.. The Guru praised him for the perfect _________ (shoot).
3. Naveen was __________ to know his result. His __________ grew when he heard about the outcome of results. (curious)
4. John _________ the TV many times. But the TV comes for __________ very frequently. (repair)
5. Water is _________ . But milk cannot be _________ (reverse).
Answer:
1) watered; water
2) shot; shot
3) curious; curiosity
4) repaired; repair
5) reversible; reversed

B) Pick out phrasal verbs beginning with ‘give’, and make sentences of your own.
1. …………………………………………..
2. …………………………………………..
3. …………………………………………..
4. …………………………………………..
Answer:
1. give up (stop) – I gave up coffee.
2. give in (put in) – Lata gave in a lot of effort for the exams.
3. give to (inclined to) – The bank gives loan to the govt’s approval.
4. give out (stop doing) – The old woman gives out and helping hand for the poor and needy as she was bankrupt.
Grammar
1. Edit the following passage correcting the underlined parts.
1. We had been longed (a) to make a trip toAndaman; and Dad makes (b) it possible for we (c) during the last summer holidaze (d).
2. In the evening, we borded (a) a ship for Port Blair, the capital at (b) the Andaman and Nicobar Islands. The ship looks (c) much bigger than our school building. It have (d) four storeys.
3. People who had come to see at (a) their friends and relatives cheered them up for (b) waving there (c) hands. My sister Am ala and I too wave (d) our hands while Mom and Dad smiled at us.
4. On the second day, we come (a) to know that we were down (b) the middle of the sea. The whether (c) was pleasant on the sea. The day was sun (d) and the sea was reflecting the clouds.
5. The medical staff were (a) busy treating the patients suffered (b) from sea-sick (c). The sanitary workers were on their job of keeping the cabins, corridoors (d) and toilets neat and clean.
6. We learnt that the inhabitance (a) of the islands were the aboriginal tribes. Some for (b) them lived far away from the civil (c) society. Despite this, the islands today looked (d) like a miniature India.
7. Open creeks running around (a) the park area were a speciality (b) attraction. We watched coral reefs, fishes by (c) different colours and sea turtles through glass-bottom (d) boats.
8. To our amazing (a), we saw some swimmers dived (b) into the sea from the motor boats. They were dressing (c) in this (d) different way.
9. Once upon a time there lived a farmer and his four daughters in an (a) village. The farmer became old out (b) sick. He wanted to teacher (c) a lesson to his daughters. He called them to him (d) bedside.
10. English is not an (a) difficult language to learn. If we learned (b) it systematically, we can learn it easily. English grammar but (c) spelling are difficult. So we have to learn it (d) carefully.
Answer:
1. a) longing b) made c) US d) holidays
2. a) boarded b) of c) looked d) had
3. a) off b) by c) their d) waved
4. a) came b) in c) weather cl) sunny
5. a) was b) suffering c) sea sickness d) corridors
6. a) iuhabitants b) of c) civilized d) look
7. a) through b) special c) of d) glass-bottomed
8. a) amazement b) diving c) dressed d) a
9. a) a b) and c) reach d) his
10. a) a b) learn e) and d) them

2. Complete the passage choosing the right words from those given below. Each blank is numbered and for each blank four choices (A), (B), (C) and (D) in the blanks.
1. We visited ________ (1) beach ________ (2) Elephant Beach. To ______ (3) amazement, we ________ (4) some swimmers diving into the sea from the motor boats.
1) A) an B) a C) the D) for
2) A) call B) called C) calling D) calls
3) A) our B) your C) their D) his
4) A) see B) few C) along D) saw
Answer:
1-C; 2-B; 3-A; 4-D
2. They ______ (1) to watch ______ (2) coral reefs and beautiful coloured fishes and sea turtles.
They stay _________ (3) a long time beneath the sea _________ (4) swim along with them.
1) A) wanted B) want C) wants D) are wanting
2) A) the B) a C) their D) those
3) A) by B) in C) of D) for
4) A) but B) or C) and D) because
Answer:
1-B; 2-A; 3-D; 4-C
3. My sister Amala and I _________ (1) a jolly ride _________ (2) the elephant. _________ (3) tasted delicious Tandoon fish and other seafoods on the islands. My mouth still ____ (4) when I remember those moments.
1) A) enjoy B) enjoying C) enjoyed D) will enjoy
2) A) on B) in C) near D) through
3) A) I B) We C) They D) It
4) A) waters B) water C) watered D) is watering
Answer:
1-C; 2-A; 3-B; 4-C
4. The park was spread ________ (1) a wide area of 15 islands. Open creeks ________ (2) through the park area were _________ (3) special attraction. We _________ (4) coral reefs, fishes of different colours and sea turtles.
1) A) in B) around C) over D) by
2) A) running B) runs C) ran D) will run
3) A) a B) the C) of D) other
4) A) watch B) are watching C) watches D) watched
Answer:
1-C; 2-A; 3-A; 4-D
5. Rajani is studying seventh dass. She is a_________ (1) student. Šhe plays tennis every day.
Last year _________ (2) won a first prize in inter-school junior tennis competitions. Her father is ______ (3) artist. Her mother _________ (4) in a factory.
1. A) clever B) cleverness C) cleverest D) best
2. A) he B) they C) she D) we
3. A) a B) an C) the D) one
4. A) works B) work C) was worked D) is worked
Answer:
1-A; 2-C; 3-B; 4-A;
6. A poor man was walking through ________ (1) forest. He saw a ________ (2) tiger which _________ (3) a gold bracelet wfth him. The tiger asked the poor man to take the bracelet. The poor man believed _________ (4) cunning words. Hë went near th tiger to take the bracelet. The tiger jumped at him and killed him.
1. A) a B) an C) the D) any
2. A) hunger B) hungry C) hungrily D) hungerly
3. A) had B) has C) have D) having
4. A) him B) his C) them D) their
Answer:
1-A; 2-E; 3-A; 4-B

A) Choose the right answer from the choices given.
1. Will you call me before you leave? ( )
A) seeking permission
B) making a suggestion
C) making a request
D) making an after
Answer:
C) making a request
2. How about going for a movie tonight? ( )
A) asking a question
B) making an offer
C) seeking permission
D) making a suggestion
Answer:
D) making a suggestion
B) Combining the following sentences using “If”.
i) Spare the red, spoil the child.
ii) Finish the exercise. Then only you can leave the class.
Answer:
i) If you spare the rod, you’ll spoil the child.
ii) If you finish the exercise, you can leave the class.
C) Fill in the blanks with simple past tense or past continuous tense of verbs.
1. They ——– for the bus when the rain ——–. (wait, fall)
2. The children ——– the cartoon show when Dad ——–. (watch, come)
3. Raju ——– ill because he ——– icecream. (fall, eat)
4. We ——– a movie before father ——–. (plan, arrive)
5. Sheetal ——– a cake when the child ——– up. (prepare, wake)
Answer:
1. were waiting, fell
2. were watching, came
3. fell, ate
4. planned, arrived
5. was preparing, woke
D) Fill in the blanks with appropriate forms of the verbs given in the brackets.
1. We ——– a programme when the lights ——–. (watch, go off)
2. Sobha and Sumanth ——– with each other when the teacher ——– the class. (fight, enter)
Answer:
1. were watching, went off
2. were fighting, entered
![]()
![]()
![]()
![]()
![]()

![]()