SCERT AP 7th Class Maths Solutions Pdf Chapter 7 Ratio and Proportion InText Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 7th Lesson Ratio and Proportion InText Questions
[Page No. 1]
There are several situations in our daily life where we use ratio and proportion. Let us look at the following pictures and answers to the given questions:
Question 1.
Can we say the ratio of speeds of Cheetah to Man?

Answer:
Speed of Cheetah = 120 kmph
Speed of a man = 20 kmph
∴ Ratio of speed of Cheetah to a man
= 120 : 20
= 6 : 1
Question 2.
What will be the ratio of heights of HematoAmir?

Answer:
Height of Hema = 150 cm
Height of Amir 75 cm
∴ Ratio of heights 150 : 75
= 2 : 1
Question 3.

Answer:
Cost of 2 Hands of banana = ₹ 80
∴ Cost of 3 Hands of banana
= \(\frac{3}{2}\) × 80 = ₹ 120
![]()
Question 4.
Do you know which aspect ratio makes constructions more attractive and beautiful?
Answer:
Golden ratio is more beautiful. It is the ratio of a line segment cut in to two pieces of different lengths such that the ratio of whole segment to that of the longer segment is equal to that of longer segment to the shorter segment.
Check your Progress [Page No. 4]
Question 1.
Write the compound ratio of the following given ratios.
(i) 3 : 5 and 4 : 3
Answer:
Given ratios are 3 : 5 and 4 : 3.
If a : b and c : d are ratios, then their compound ratio is product of antecedents : product of extremes.
that is a × c : b : d
3 × 4 : 5 × 3
12 : 15
∴ Compound ratio = 4 : 5
(ii) 8 : 3 and 6 : 5
Answer:
Given ratios are 8 : 3 and 6 : 5.
If a : b and c : d are ratios, then their compound ratio is product of antecedents : product of extremes, that is
a × c : b : d
8 × 6 : 3 × 5
∴ Compound ratio = 16 : 5
(iii) 2: 1 and 8: 7
Answer:
Given Ratios are 2 : 1 and 8 : 7.
If a : b and c: d are ratios, then their compound ratio is product of antecedents : product of extremes that is a × c : b : d
2 × 8 : 1 × 7
16 : 7
∴ Compound ratio= 16 : 7
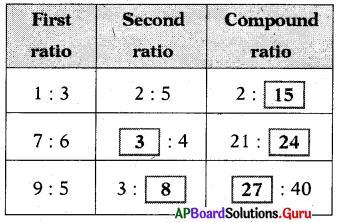
Question 2.
Fill in the boxes with correct answers.
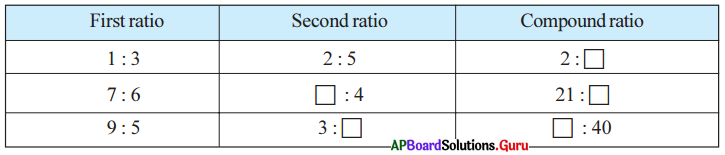
Answer:
[Page No. 6]
Discuss and answer the following questions related to real-life situations:
Question 1.
If the cost of 3 ball pens is ₹ 15, then what is the cost of 6 such pens?
Answer:
3 : 15 : : 6 : cost
Cost x 3 = 15 × 6
∴ Cost = \(\frac{15 \times 6}{3}\) = ₹ 30
Question 2.
In a school, for implementing ‘Mid day Meal’ scheme for class VII of 40 students they need 6 kgs of rice for one day.
(i) How much rice is needed for 6 days?
Answer:
Rice required for 40 students for one day = 6 kgs
Rice required for 6 days = 6 × 6 = 36 kg
(ii) How much rice is needed for 10 days?
Answer:
Rice required for 10 days = 10 × 6 = 60 kg
(iii) How much rice is needed for 5 days?
Answer:
Rice required for 5 days = 5 × 6 = 30 kg
Let’s Explore [Page No. 6]
Question 1.
Given below the number of workers working for construction of a house and their wages in total.

Answer:

![]()
Let’s Think [Page No. 7]
Question 1.
If the cost of 4 note books is 80. What would be the cost of7 note books? The above problem can be solved by using unitary method. Can you solve? How? Think.
Answer:
Given the cost of 4 note books = ₹ 80
Cost of 1 note book = 80 ÷ 4 = ₹ 20
Cost of 7 note books = ₹ 20 × 7
= ₹ 140
Check Progress [Page No 7]
Question 1.
Fill in the blanks, if the given quantities are in direct proportion.

Answer:

Let’s’ Do Activity [Page No. 8]
Take a clock and fix Its minute hand at a particular number on clock (if it is 12 It will be easy). Then find and note the angles made by minute hand in every 15 minutes interval of time:


Check whether they are in direct proportion or not?
Answer:

15 : 30 and 90 : 180
Here 1 :2 = 1 :2
If ratios are equal, then they are in direct proportion.
So, time passed and angle are in direàt proportion.
Let’s Think [Page No. 8]
Question 1.
What is the angle made by minutes hand in a minute?
Answer:
We know angle made by minutes hand in 15 m = 90°
Let angle made by minutes hand in 1 m = x°
Then 15 : 1 = 90°: x°
If the ratios are equal,
The product of means = The product of extremes
⇒ 15 × x = 1 × 90°
⇒ \(\frac{15 x}{15}=\frac{90^{\circ}}{15}\)
⇒ x = 6°
∴ Angle made by minutes hand in 1 minute = 6°
Question 2.
What is the angle made by hours hand in one minute?
Answer:
We know angle made by hours hand in 1 hour (60 minutes) = 30°
Let angle made by hours hand 1 minute = x°
Then 60 : 1 = 30°: x°
If the ratios are equal,
The product of means = The product of the extremes
⇒ 60 × x = 1 × 30
⇒ \(\frac{60 x}{60}=\frac{30}{60}=\frac{1}{2}\)
⇒ x = \(\frac{1}{2}\) (or) 0.5°
∴ Angle made, by hours hand in 1 minute = \(\frac{1}{2}\)° (or) 0.5°
![]()
Check your Progress [Page No. 9]
Question 1.
Fill in the blanks if the given quantities are in inverse proportion.

Answer:

Check your Progress [Page No. 13]
Question 1.
Analyse how the three quantities given below are related and find ‘x’.
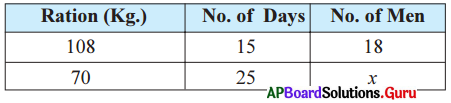
Answer:
From the above,
- Ration and the number of days are in inversely proportional.
- Ration and number of men are in directly proportional.
- Number of men is depends on both Ration and number of days.
So we have to take compound ratio of 108 : 70 and 25 : 15
i. e., 108 × 25 : 70 × 15
∴ 18 : x = 108 × 25 : 70 × 15
If the ratios are equal.
The Product of means = The Product of extremes
⇒ 108 × 25 × x = 18 × 70 × 15
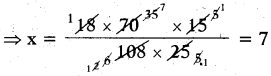
∴ x = 7
Let’s Think [Page No. 18]
Question 1.
A man buys chocolates 10 for 10 rupees and sells them at 10 for ₹ 12. Does this result profit or loss ? What percent?
Answer:
Given cost price of 10 chocolates = ₹ 10
Selling price of 10 chocolates = ₹ 12
SP > CP, then man gets profit.
Profit = S.P – C.P
= 12 – 10 = ₹ 2
We know profit percent

Profit percentage = 20%
Question 2.
If a shopkeeper bought sofa sets and increases their prices by 50% and sell at 50% less, is it a loss or gain?
Answer:
Let the cost price of sofa set = ₹ 100
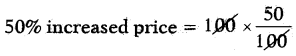
= ₹ 5o
Total printed price = ₹ 100 + ₹ 50
= ₹ 150
Loss percent = 50%
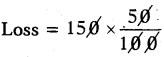
Loss = ₹ 75
Selling price Printed Price – Loss
= 150 – 75 = ₹ 75
C.P= ₹ 100; S.P = ₹ 75
and C.P > S.P
So, the shopkeeper will get loss of 25%.
![]()
Check Your Progress [Page No. 20]
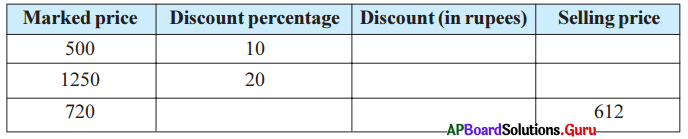
Answer:

Check Your Progress [Page No. 24]

Answer:

Let’s Think [Page No. 24]
Question 1.
At what rate per annum will the principle doubles in 10 years?
Answer:
Method 1:
Let the principle = 100
Interest rate = x% ; Time = 10 years
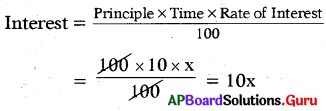
Amount = Principle + Interest
= Double the principle
= 100 + 10x = 200
⇒ 100 + 10x – 100 = 200 – 100
⇒ 10x = 100
⇒ \(\frac{10 x}{10}=\frac{100}{10}\)
⇒ x = 10%
∴ Rate of interest = 10%
Method 2:
Let the principle =?
Rate of Interest = R%
T = 10 years
Given that A = 2P = P + P [∵ A = P + I]
∴ I = P
∴ \(\frac{\mathrm{P} \times \mathrm{T} \times \mathrm{R}}{100}\) = P
⇒ \(\frac{\mathrm{P} \times 10 \times \mathrm{R}}{100}\) = P
R = 10%
∴ The principle become double in 10 years at 10% rate of interest.
![]()
Question 2.
At what rate per annum will the principle be 4 times in 15 years?
Answer:
Method 1:
Let the principle = ₹ 100
Interest rate = x %
Tirne = 15 years
Interest = \(\frac{\mathrm{PTR}}{100}\)
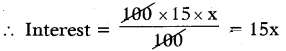
Amount = Principle + Interest
= 4 times the principle
= 100 + 15x = 400
⇒ 100 + 15x – 100 = 400 – 100
⇒ 15x = 300
⇒ \(\frac{15 x}{15}=\frac{300}{15}\) = 20%
∴ x = 20%
Method 2:
Let the principle = P
Time = 15 years
A = 4timesP = 4P
⇒ A = P + 3P
But A = P + I
So I = 3P
We know that I = \(\frac{\text { PTR }}{100}\)
⇒ 3P = \(\frac{P \times 15 \times R}{100}\)
⇒ R = \(\frac{100 \times 3}{15}\) = 20%
∴ The principle become 4 times in 15 years at 20% rate of interest.
Examples:
Question 1.
Find the compound ratio of 8 : 7 and 9 : 13.
Answer:
Given ratio = 8 : 7 :: 9 : 13
Compound ratio = 8 × 9 : 7 × 13 = 72 : 91
(∵ Compound ratio product of antecedent product consequents).
Question 2.
Two friends Prabhu and Suresh started a business with ₹ 1,00,000 each. After 3 months Suresh left the business. At the end of the year, there was a profit of ₹ 20,000. Calculate the profits shared by Prabhu and Suresh?
Answer:
Here Prabhu and Suresh started a business with ₹ 1,00,000.
Prabhu continued till the end of the year.
Suresh continued only for 3 months.
The ratio of the contributions
= 100000: 100000 = 1 : 1
Ratio of their period of business
= 12 : 3 = 4 : 1
So, their profits sho’uld be divided on the basis of compound ratio
Compound ratio = 1 × 4 : 1 × 1
Profit = ₹ 20,000
Total parts= 4 + 1 = 5
Suresh’s profit = 20000 × \(\frac{1}{5}\)
= ₹ 4000
Prabhus profit = 20000 – 4000
= ₹ 16000
![]()
Question 3.
Rani started a beauty parlour with an amount ₹ 75,000. After 4 months, Vani also joined with Rani with an amount ₹ 50,000. After one year, they got a profit of ₹ 52,000. Calculate the profits shared by Rani and Vani.
Answer:
Rani’s investment = ₹ 75,000
Rani’s period in business = 1 year = 12 months
Vani’s investment = ₹ 56,000
Vani’s period in business = 8 months
The ratio of investments of Rani to Vani = 75,000 : 50,000 = 3:2
The ratio of periods of business of Rani to Vani =12:8 = 3:2
The profit should be distributed on the, basis of compound ratio.
Compound ratio = 3 ×. 3 : 2 × 2
= 9 : 4
Profit = ₹ 52,000
Total parts = 9 + 4 = 13
Rani’s profit = 52,000 × \(\frac{9}{13}\)
= ₹ 36000
Vani’s profit = 52,000 – 36,000 = ₹ 16,000
Question 4.
If 3 : 4 and 9 : x are in direct proportion, then what is the value of x?
Answer:
If 3 : 4 and 9 : x are in direct proportion, then their ratio is constant.
∴ \(\frac{3}{4}=\frac{9}{x}\)
⇒ 3 × x = 4 × 9
⇒ x = \(\frac{4 \times 9}{3}\) = 12
Question 5.
If the cost of 4 note books is ₹ 80. What would be the cost of 7 note books?
Answer:
We know that as number of note books increases, the cost also increases such that the ratio of number of note books and the ratio of their costs will remain the same. That means here number of note books and the cost are in direct proportion.
Let the cost of 7 note books be ‘x’.
Then, 4 : 80 = 7 : x
If the ratios are equal, the product of means = The product of the extremes
4 × x = 80 × 7
⇒ x = \(\frac{80 \times 7}{4}\) = ₹ 140
Thus, the cost of 7 note book is equal to ₹ 140.
Question 6.
The scale of a map is given as 1 : 30000. If two cities are 20 cm apart on the map, then o-j, . find the actual distance between them.
Answer:
Let the actual distance be ‘x’ cm. Since the distance on the map is directly proportional to the actual distance.
1 : 30000 = 20 : x
If the ratios are equal, the product of means = The product of the extremes
∴ 1 × x = 30,000 × 20
⇒ x = 6,00,000 cm = 6 km. [1,00,000 cm = 1000 m = 1 km.]
Thus, two cities which are 20cm apart on the map are actually 6 km away from each other.
Question 7.
If 4, 7 and 2, x are inverse proportion, then what is the value of x?
Answer:
4, 7 and 2, x are in inverse proportion . Therefore, 4 × 7 = 2 × x
⇒ x = \(\frac{4 \times 7}{2}\) = 14
![]()
Question 8.
If 18 workers can build a wall in 12 days, how many days will eight workers take to build the same wall?

Answer:
If the number of workers decreases, the time taken to build the wall increases in the same proportion.
So, number of workers and the number of days to complete work are in inverse proportion.
Let the number of days to complete the work be ‘x’.
| Number of workers | Number of days |
| 18 | 12 |
| 8 | x |
By taking inverse proportion,
18 : 8 = x : 12
Then,
∴ 18 × 12 = 8 × x
⇒ 8 × x = 18 × 12
⇒ x = \(\frac{18 \times 12}{8}\) = 27days
∴ Eight workers can complete the will in 27 days.
Observe this:
In inverse Proportion, product is always constant.
∴ 18 × 12 = 8 × x
⇒ 8 × x = 18 × 12
⇒ x = \(\frac{18 \times 12}{8}\) = 27days
Question 9.
4 Pumps are required to fill a tank in 1 hr 30 min. How long will it take if only 3 pumps of the same type are used?

Answer:
Let the time be ‘x’.
1 hr 30min = 60 + 30 = 90 minutes ,
If the number of pumps are decrease, the time taken to fill the tank increases.
So, the number of pumps and time taken to fill the tank are in inverse proportion.
| Number of pipes | Time taken to fill (min) |
| 4 | 90 |
| 3 | x |
By taking inverse proportion,
4 : 3 = x : 90
Thus,
∴ 4 × 90 = 3 × x
⇒ 3 × x = 4 × 90
⇒ x = \(\frac{4 \times 90}{3}\) = 120 min
∴ 3 pumps will fill the tank in 120 min or 2 hrs.
Observe this:
In inverse proportion, product is always constant
∴ 4 × 90 = 3 × x
⇒ 3 × x = 4 × 90
⇒ x = \(\frac{4 \times 90}{3}\) = 120 min
Question 10.
If 30 persons use 40 kg. of sugar in 10 days, find in how many days 80 persons will use 320 kg. of sugar? How can we solve?
Answer:
Here, the 3 quantities are persons, weight and number of days.
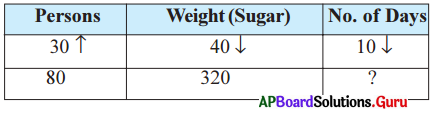
From the above comparison mustbe in between unknown form to know form.
- Here days and persons are in inverse we denote it with Tmark.
- Here days and sugar are in direct proportion we denote it with 4r mark.
Here number of days is depends on both persons and weight of sugar. So we have to take compound ratio of 80 : 30 and 40 : 320.
∴ 10 : x = 80 × 40 : 30 × 320 = 3200 : 9600
Since the ratios are equal, the product of extremes is equal to product of means.
10 : x = 3200 : 9600 ⇒ 10 × 9600 = x × 3200
⇒ x × 3200 = 10 × 9600 ⇒ x = \(\frac{10 \times 9600}{3200}\) = 30
Question 11.
8 painters can paint a wall of 160m long in 5 days. How many painters are required to paint 240kn. wall in 10 days?
Answer:
Here we have three quantities – number of painters, length of wall and number of days.
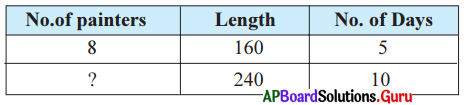
Number of painters, is directly proportional to length of the wall.
Number of painters is inversely proportional to the number of days.
Since the number of painters depends both on length of wall and number of days. We will take the compound ratio of 160 : 240 and 10 : 5 1
∴ 8 : x = 160 × 10 : 240 × 5
Since the ratios are equal, product of means is equal to product of extremes
8 : x = 160 × 10 : 240 × 5
⇒ x × 160 × 10 = 8 × 240 × 5
⇒ x = \(\frac{8 \times 240 \times 5}{160 \times 10}\) = 6
Hence the required number of painters = 6
![]()
Question 12.
195 men working 10 hours a day can finish a job in 20 days. How many men are employed to finish the job in 15 days if they work 13 hours a day?
Answer:
Here we have three quantities – number of workers, number of hours and number of days.
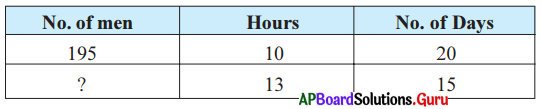
Here the number of workers inversely proportional to number of hours per day.
Here the number of workers inversely proportional to number of days.
Since number of workers depends on both number of hours and number of days, we will take compound ratio of 13 : 10 and 15 : 20.
Since the ratios are equal, the product of means is equal to product of extremes.
195 : x = 13 × 15 : 20 × 10
⇒ x × 13 × 15 = 195 × 20 × 10
⇒ x = \(\frac{195 \times 20 \times 10}{13 \times 15}\) = 200
Hence the required number of workers = 200
Question 13.
Express the following percentages as fraction, decimal and In ratio.
(i) 45%
Answer:
45% = \(\frac{45}{100}=\frac{9}{20}\)(Fraction)
= 0.45 (decimal form)
= 9:20 (ratio)
(ii) 62%
Answer:
62% = \(\frac{62}{100}=\frac{31}{50}\) = (Fraction)
= 0.62 (decimal form)
= 31:50 (ratio)
Question 14.
Find 24% of 150 and àlso the remaining of that number.
Answer:
24% of 150 = \(\frac{24}{100}\) × 150 = 36
The remaining of that number
= 150 – 36 = 114
Question 15.
Raghu bought pens for 400 and he sold them for ₹ 480 what Is his profit or loss percent?
Answer:
Jyothi solved It this way:
Pen C.P of = ₹ 400, S.P = ₹ 480
S.P > C.P.
So, Raghu gets a profit P = 480 – 400 = ₹ 80
Profit Percentage = \(\frac{80}{400}\) × 100 = 20%
Anwar solved it this way :
Raghu’s Profit = S.P. – C.P = 480 – 400 = ₹ 80
The ratio of profit and cost or the fraction is \(\frac{80}{400}\)
∴ Profit Percentage = \(\frac{80}{400}\) × 100 = 20%
Suresh solved it using proportion :
When C.P is ₹ 400, the profit is ₹ 80 C.P. is ₹ 100, let the profit be ₹ x.
Here C.P and profit are in direct proportion.
x : 80 = 100 : 400 ⇒ \(\frac{x}{80}=\frac{100}{400}\)
⇒ x × 400 = 100 × 80
⇒ x = \(\frac{100 \times 80}{400}\) = 20%
Profit = 20 per 100
Profit Percentage = 20%
Question 16.
Ramana bought a cycle for ₹ 1200 and sold it to his friend Rehman for ₹ 900, then what is Ramanas profit or loss percentage?
Answer:
Here Ramana’s Cost price = ₹ 1200
Selling price = ₹ 900
S.P < C.P, then Ramana got loss
Loss = C.P – S.P = 1200 – 900 = ₹ 300
Loss percentage = \(\frac{300}{1200}\) × 100 = 25%
![]()
Question 17.
If John buys a ear for ₹ 1,50,000 and gains 10% on selling it. Then find the selling price.

Answer:
Cost Price = ₹ 1,50,000
Gain % = 10%
Profit = 10% of ₹ 1,50,000
= \(\frac{10}{100}\) × 150000 = ₹ 15000
Selling Price = C.P. + Profit
= ₹ 1,50,000 + ₹ 15,000
= ₹ 1,65,000
This can be solved using proportion:
Gain 10% means
If CP is ₹ 100,the gain is ₹ 10
Thus S.P = 100 + 10 = 110
Now, here C.P = ₹ 1,50,000
Let S.P = x
CP and SP are directly proportional.
\(\frac{110}{100}=\frac{x}{1,50,000}\)
\(\frac{x}{1,50,000}=\frac{110}{100}\)
x = \(\frac{1,50,000 \times 110}{100}\) = ₹ 1,65,000
Question 18.
Kiran sold a refrigerator for ₹ 16800 at a gain of 12%. Then what is the cost price of it?

Answer:
Roopa did the problem uslnj unitary method:
S.P = ₹ 16800 ; Gain% = 12%
If CP is ₹ 100, then Profit is ₹ 12 and thus S.P = ₹ 112
So when S.P is ₹ 112, then C.P is ₹ 100
When S.P is One Rùpee, C.P is \(\frac{110}{112}\) .
Here S.P is ₹ 16800
So, C.P = \(\frac{110}{112}\) × 16800 = ₹ 15000
Sneha solve did the prot1em using proportion as follows:
Gain % = 12% ;S.P = ₹ 16800
If C.P is ₹ 100 then profit is ₹ 12, thus SP = ₹ 12
here S.P = ₹ 16800
C.P be x
C.P and S.P are directly proportional.
∴ \(\frac{x}{16800}=\frac{100}{112}\)
⇒ x = \(\frac{100 \times 16800}{112}\) = ₹ 15000
Question 19.
The cost of an article goes down every year by 10% of its previous value. Find its original cost, if its cost after 2 years is ₹ 32400.
Answer:
Let the cost at the beginning of 1st year be ₹ 100. At the beginning of,2nd year i.e at the end of 1st year it will be decreased by 10% means cost will be ₹ 90.
At the end of 2nd year i.e at the beginning of 3rd year it will be reduced by 10%
i. e. ₹ 90 is reduced by 10%.
90 – 9 = ₹ 81
If the cost of object is ₹ 100 at the beginning, then after 2 years it’s cost will be ₹ 81.
Let the cost of the object ₹ ‘x’ at the beginning, after 2 years it’s cost is ₹ 32,400 .
Thus ratio of original costs = ratio of costs after 2 years
⇒ x : 100 = 32400 : 81
⇒ \(\frac{x}{100}=\frac{32400}{81}\)
⇒ x = \(\frac{32400 \times 100}{81}\) = ₹ 40000
![]()
Question 20.
Find discount if,
(i) marked price is ₹ 450, selling price = ₹ 415
Answer:
Discount = marked price – selling price ⇒ 450 – 415 = ₹ 35.
(ii) marked price = ₹ 810, selling price = ₹ 765.
Answer:
Discount = marked price – selling price ⇒ 810 – 765 = ₹ 45.
Question 21.
If discount is ₹ 40, marked price is ₹ 400, then find discount percentage.
Answer:
Discount = ₹ 40, marked price = ₹ 400,
then discount percentage = \(\frac{40}{400}\) × 100 = 10
Question 22.
A shopkeeper marks his goods 20% above the cost price and allows a discount of 10% on them. What percent does he gain?
Answer:
Let the cost price be ₹ 100.
Then the marked price = 100 + 20 = ₹ 120
Discount = 10%, so discount = x 120 = 12% /
SP = Marked price – Discount = ₹ 120 – ₹ 12 = ₹ 108
Gain = \(\frac{8}{100}\) × 100 = 8%
The shopkeeper gains 8% after discount.
Question 23.
Calculate simple interest and the total amount, if
(i) principal = ₹ 5000, time = 2 years, rate = 10%
Answer:
Simple interest
I = \(\frac{\mathrm{P} \times \mathrm{T} \times \mathrm{R}}{100}=\frac{5000 \times 2 \times 10}{100}\) = ₹ 1000
Total amount = principal + interest = 5000 + 1000 = ₹ 6000
(ii) principal = ₹ 25000, time = 3 years, rate = 12%
Answer:
Simple interest = \(\frac{\mathrm{P} \times \mathrm{T} \times \mathrm{R}}{100}=\frac{25000 \times 3 \times 12}{100}\) = ₹ 9000
Total amount = principal + interest = 25000 + 9000 = ₹ 34000
Question 24.
If Raheem borrowed a sum of ₹ 25000 at a rate 10% per annum, what is the simple interest and total amount he has to pay for 3 years?
Answer:
Rajesh did like this :
Principal = ₹ 25000 ; Time = 3 years ; Rate of interest = 10%
Simple interest = I = \(\frac{\mathrm{P} \times \mathrm{T} \times \mathrm{R}}{100}=\frac{25000 \times 3 \times 10}{100}\) = ₹ 7500
Total amount = ₹ 25000 + ₹ 7500 = ₹ 32500
Sangeetha did like this :
For 1 year we have to pay 10%,
for 3 years we have to pay 3 × 10 = 30% as interest.
Interest = \(\frac{30}{100}\) × 25000 = ₹ 7500
Total amount = ₹ 25000 + ₹ 7500 = ₹ 32500
![]()
Question 25.
What sum will yield an interest of ₹ 6000 at 9% per annum in 3 years 4 months?
Answer:
S.I = ₹ 6000 ; R = 9%

Question 26.
At what rate per annum will ₹ 70000 yield an interest of ₹ 14000 in 2\(\frac{1}{2}\) years?
Answer:
Principal = ₹ 70000 ; Time = 2\(\frac{1}{2}\)years = \(\frac{5}{2}\) years ; Simple interest = ₹ 14000

