SCERT AP 7th Class Maths Solutions Pdf Chapter 7 Ratio and Proportion Unit Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 7th Lesson Ratio and Proportion Unit Exercise
Question 1.
If the cost of 7 toys is ₹ 1575, then what would be the cost of 6 such toys?
Answer:
We know that the number of toys decreases, the cost also decreases such that the ratio of the number of toys and the ratio of their costs will remain the same. That means here number of toys and the cost are in direct proportion.
Let the cost of 6 toys be x.
Then 7 : 1575 = 6 : x
If the ratios are equal, the product of extremes = Product of means
⇒ 7 × x = 1575 x 6
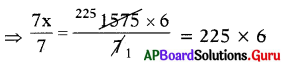
⇒ x = ₹ 1350
∴ Cost of 6 toys is ₹ 1350.
![]()
Question 2.
A boy went to a hotel and wants to buy 5 plates of Idly worth ₹ 24 each. After, going to Hotel he observed that rates of Idly were increased to ₹ 30. Now if the boy wants to buy idlies, how many plates of idlies he can buy with the same amount?
Answer:
If the cost of idly increases number of plates decreases.
So, cost of idly and number of plates are in inverse proportion.
Let number of plates at ₹ 30 for the same amount is x.
| Cost of each Idly Plate | Number of Plates |
| 24 | 5 |
| 30 | x |
By taking inverse proportion, 24 : 30 = x : 5
Then, Product of means = Product of extremes
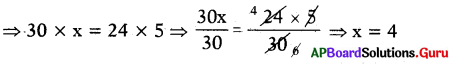
Number of Plates at ₹ 30 for the same amount is 4.
Question 3.
Raju covers a distance of 28 kilometers in 2 hours. Find the time taken by him to cover a distance of 56 km with the same speed.
Answer:
We know that as number of kilometers (distance) increases the time taken also increases with the same speed. That means distance and the time taken are in direct proportion.
Let the time taken to cover the 56 km distance is x hours.
Then 28 : 2 = 56 : x
If the ratios are equal, the product of extremes = the product of means
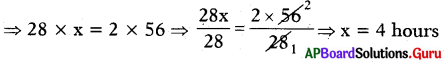
The time taken to cover the 56 km distance is 4 hours.
Question 4.
24 men working at 8 hours per day can do a piece of work in 15 days. In how many days 20 men working 9 hours per day do the same work?
Answer:
Here, we have three quantities number of workers, number of hours and number of days.
| Number of Men | Hours | Number of Days |
| 24 | 8 | 15 |
| 20 | 9 | x |
Here the number of worker’s inversely proportional to number of hours perday.
Here the number of workers inversely proportional to number of days.
Let the number of days be ‘x’.
Since number of workers depends on both number of hours and number of days, we will take compound ratio of
24 : 20 and 8 : 9 is 24 × 8 : 20 × 9
Since the ratios are equal,
The product of means = The product of extemes
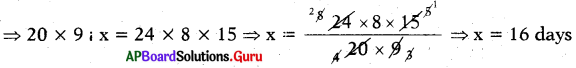
∴ Number of days required to complete 20 men at 9 hours per day is 16.
Question 5.
Out of 15000 voters in a constituency, 60% of the voters voted. Find the number of people not voted in the constituency.
Answer:
Given number of voters in the constituency = 15000 Percentage of voters voted = 60 %
Number of people voted = 60% of 15000
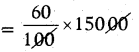
Number of people voted in the constituency = 9000
Number of people not voted = 15000 – 9000
∴ Number of people not voted = 6000
![]()
Question 6.
A shopkeeper bought a suitcase for ₹ 950 and sold it for ₹ 1200. Find its profit or loss percentage.
Answer:
Given cost price of suitcase = ₹ 950
Selling price of suitcase = ₹ 1200
S.P > C.P
So, shopkeeper got profit.
Profit = S.P – C.P = 1200 – 950 = ₹ 250
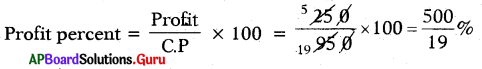
∴ Profit percent = 26\(\frac{6}{19}\)%.
Question 7.
On selling a mobile for ₹ 4500, the shopkeeper losses 10%. For what amount should be selling it to gain 15%?
Answer:
Method 1 :
Given selling of mobile = ₹ 4500
Loss = 10%
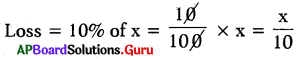
S.P = C.P – Loss
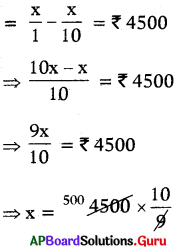
∴ x = 5000
Method 2:
Let the C.P of mobile = 100%
S.P at a loss of 10% = (100 – 10)%
= ₹ 4500
90% of C.P = ₹ 450O
S.P at a gain of 15% = (100 + 15)%.
= 115%
So, if 90% of CP = ₹ 4500
115% of CP = ?
s.p= \(\frac{115}{90}\) × 4500= ₹ 5750
∴ Cost price of mobile = ₹ 5000
If he gain 15%.
Gain = 15% of 5000
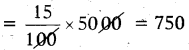
S.P = C.P + Gain = 5000 + 750
∴ Selling price of Mobile = ₹ 5750
Question 8.
A carpenter allows 15% discount on his goods. Find the markedprice of a chair which is sold by him for ₹ 680.
Answer:
Given selling price = ₹ 680
Discount percent = 15%
Let marked price = x

Note:
85% of M.P = ₹ 680
100% of M.P = \(\frac{100}{85}\) × 680
= ₹ 800.
![]()
Question 9.
What Is the simple Interest accrued on asum of ₹ 75000 at the rate of 11% for 3 years? Find the total amount.
Answer:
Given Principle = ₹ 7500
Rate of Interest = 11%
Time = 3 years
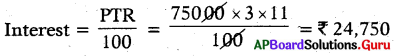
Total amount = Principle + Interest = ₹ 75000 + ₹ 24750
∴ Total amount = ₹ 99,150
