AP State Syllabus AP Board 6th Class Maths Solutions Chapter 5 Fractions and Decimals Ex 5.3 Textbook Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 5th Lesson Fractions and Decimals Ex 5.3
Question 1.
Find the reciprocal of each of the following fractions.
i) \(\frac{5}{9}\)
ii) \(\frac{12}{7}\)
iii) 2\(\frac{1}{5}\)
iv) \(\frac{1}{8}\)
v) \(\frac{13}{11}\)
vi) \(\frac{8}{3}\)
Answer:

(Reciprocal of a fraction \(\frac{a}{b}\) is \(\frac{b}{a}\)).
![]()
Question 2.
Simplify:
i) 15 ÷ \(\frac{3}{4}\)
ii) 6 ÷ 1\(\frac{4}{7}\)
iii) 3 ÷ 2\(\frac{1}{3}\)
iv) \(\frac{4}{9}\) ÷ 15
v) 4\(\frac{3}{7}\) ÷ 14
Answer:
i) 15 ÷ \(\frac{3}{4}\)
While dividing a whole number by a fraction, multiply the whole number with the reciprocal of the fraction.
Thus,
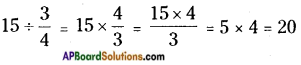
ii) 6 ÷ 1\(\frac{4}{7}\)
While dividing a whole number by a mixed fraction, first convert the mixed fraction into improper fraction and then multiply the whole number with the recipro¬cal of the improper fraction.
Thus,
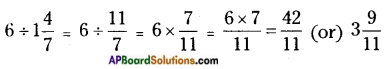
iii) 3 ÷ 2\(\frac{1}{3}\)
While dividing a whole number by a mixed fraction, first convert the mixed fraction into improper fraction and then multiply the whole number with the reciprocal of the improper fraction.
Thus,
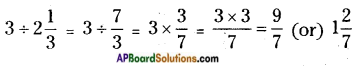
![]()
iv) \(\frac{4}{9}\) ÷ 15
While dividing a proper fraction by a whole number, multiply the proper fraction with the reciprocal of a whole number.
Thus,
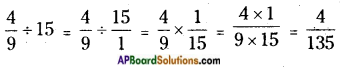
v) 4\(\frac{3}{7}\) ÷ 14
While dividing mixed fraction by a whole number first convert the mixed fraction into improper fraction and then multiply the improper fraction with the reciprocal of a whole number.
Thus,
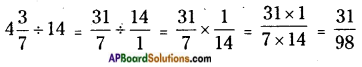
Question 3.
Find:
i) \(\frac{4}{9}\) ÷ \(\frac{2}{3}\)
ii) \(\frac{4}{11}\) ÷ \(\frac{8}{11}\)
iii) 2\(\frac{1}{3}\) ÷ \(\frac{3}{5}\)
iv) 5\(\frac{4}{7}\) ÷ 1\(\frac{3}{10}\)
Answer:
i) \(\frac{4}{9}\) ÷ \(\frac{2}{3}\)
While dividing a proper fraction by a proper fraction, multiply the proper fraction with the reciprocal of the fraction.
Thus,
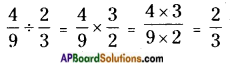
ii) \(\frac{4}{11}\) ÷ \(\frac{8}{11}\)
While dividing a proper fraction by a proper fraction, multiply the proper fraction with the reciprocal of the fraction.
Thus,
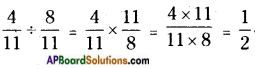
iii) 2\(\frac{1}{3}\) ÷ \(\frac{3}{5}\)
While dividing a mixed fraction by a proper fraction, first convert the mixed fraction into improper fraction, then multiply it with the reciprocal of the proper fraction.
Thus,
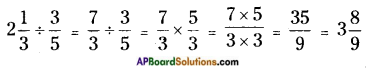
![]()
iv) 5\(\frac{4}{7}\) ÷ 1\(\frac{3}{10}\)
While dividing a mixed fraction by a mixed fraction first convert the two mixed fraction into improper fraction, then multiply the improper fraction with the reciprocal of the second improper fraction.
Thus,
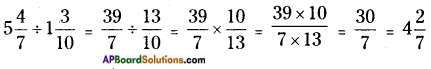
Question 4.
The product of two numbers is 25\(\frac{5}{6}\). If one of the number is 6\(\frac{2}{3}\). Find the other.
Answer:

Question 5.
By what number should 9\(\frac{3}{4}\) be multiplied to get 5\(\frac{2}{3}\)?
Answer:
Given one number = 9\(\frac{3}{4}\) = \(\frac{39}{4}\)
Product = 5\(\frac{2}{3}\) = \(\frac{17}{3}\)
\(\frac{39}{4}\) × Required Number = \(\frac{17}{3}\)
Required Number = \(\frac{17}{3}\) ÷ \(\frac{39}{4}\)
= \(\frac{17}{3}\) × \(\frac{4}{39}\)
= \(\frac{17 \times 4}{3 \times 39}\)
= \(\frac{68}{117}\)
Number to be multiplied = \(\frac{68}{117}\)
Question 6.
A bucket contains 34\(\frac{1}{2}\) litres of water. How many times do you get 1\(\frac{1}{2}\) litres of water?
Answer:
Capacity of Bucket = 34\(\frac{1}{2}\) litres = \(\frac{69}{2}\) litres
Capacity required = 1\(\frac{1}{2}\) = \(\frac{2 \times 1+1}{2}\) =\(\frac{3}{2}\)
Number of times we get = \(\frac{69}{2}\) ÷ \(\frac{3}{2}\) = \(\frac{69}{2}\) × \(\frac{2}{3}\) = 23 times.
![]()
Question 7.
The cost of 3\(\frac{3}{4}\) kg. of sugar is Rs. 121\(\frac{1}{2}\). Find its cost per 1 kg.
Answer:
Cost of 3\(\frac{3}{4}\) kg of sugar = Rs. 121\(\frac{1}{2}\)
Cost of 1kg of sugar

Cost of 1kg of sugar = Rs. 32.40.
Question 8.
The length of a rectangular field is 12\(\frac{1}{4}\) m. and its area is 65\(\frac{1}{3}\)m2. Find its breadth.
Answer:
Length of a rectangular field = 12\(\frac{1}{4}\) = \(\frac{49}{4}\) m
Breadth of a rectangular field = ?
Area of a rectangular field = 65\(\frac{1}{3}\) = \(\frac{196}{3}\) sq.m
length × breadth = Area of a rectangular

∴ Breadth of a rectangular field = 5\(\frac{1}{3}\) m.
