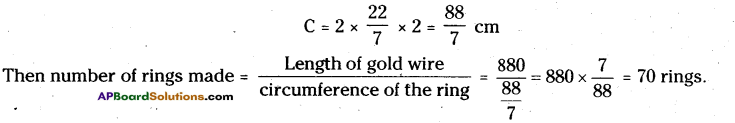Class 6

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 9 2D-3D Shapes Unit Exercise Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 9th Lesson 2D-3D Shapes Unit Exercise

Question 1.
Give examples for each shape in the table.

Sphere	Cylinder	Cube	Cone
1.
2.
3.	.

Solution:

Sphere	Cylinder	Cube	Cone
1. Marbles	Chalk piece	Dice	Heap of rice
2. Laddu	Road roller	Ice cube	Tent
3. Tennis ball	Pillar of building	Rubic cube	Joker cap

Question 2.
Look at the adjacent figure and answer the following questions,
(i) What is the name of the triangle?
(ii) Write all sides, angles and vertices of the triangle.
Solution:
i) Name of the given triangle is ΔPQR.
ii) The sides of ΔPQR are \(\overline{\mathrm{PQ}}, \overline{\mathrm{QR}}\) and \(\overline{\mathrm{PR}}\) .
The angles of ΔPQR are ∠P, ∠Q and ∠R.
The vertices of ΔPQR are P, Q and R.

Question 3.
Look at the adjacent figure and answer the following questions.
(i) Write the name of this polygon.
(ii) Write the pairs of adjacent sides and adjacent angles.
(iii) Write all vertices, pairs of opposite sides and pairs of opposite angles.
Solution:
i) Name of the given polygon is quadrilateral EFGH.
ii) EH and FG are pair of adjacent sides of EF.
EF’ and GH are pair of adjacent sides of FG.
FG and EH are pair of adjacent sides of GH.
EF and HG are pair of adjacent sides of EH.
Adjacent angles of E are ∠H and ∠F.
Adjacent angles of F are ∠E and ∠G.
Adjacent angles of G are ∠F and ∠H.
Adjacent angles of H are ∠G and ∠E

iii)Vertices of the quadrilateral EFGH are E, F, G and H.
Opposite side of EF is GH.
Opposite side of FG is EH.
Pairs of opposite angles are ∠E, ∠G and ∠F, ∠H.

Question 4.
Say true or false.
(i) We can locate only one centre in a circle. [ ]
(ii) All chords are called diameters. [ ]
(iii) A square pyramid has squares as its faces. [ ]
Solution:
i) True
ii) False
iii) False

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 9 2D-3D Shapes Ex 9.4 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 9th Lesson 2D-3D Shapes Ex 9.4

Question 1.
Write the shapes of the following.
(i) A brick (ii) A road roller (iii) Foot ball (iv) Joker cap
Solution:
i) Shape of a brick is cuboid.
ii) Shape of a road roller is cylinder.
iii) Shape of a foot ball is shpere.
iv) Shape of a joker cap is cone.

Question 2.
Fill in the blanks.
(i) The shape of heap of grain
(ii) The shape of a dice
(iii) The shape of a bubble
(iv) The shape of a candle
Solution:
i) Cone ii) Cube iii) Sphere

Question 3.
Match the following.

Solution:

Question 4.
Fill in the table.

Shape	No.of faces	No. of vertices	No. of edges
Cube
Triangular prism
Square pyramid
Cuboid

Verify Euler’s Formula for the data in the table.

We know that, the F + V = E + 2is Euler’s formula.
In the above table given shapes satisfy the Euler’s formula.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 9 2D-3D Shapes Ex 9.3 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 9th Lesson 2D-3D Shapes Ex 9.3

Question 1.
Look at the given quadrilateral and answer the following questions.
i) What are the sides of the given quadrilateral?
ii) What is the opposite side of \(\overline{\mathrm{AB}}\) ?
iii) What is the opposite vertex of B?
iv) What is the opposite angle of ∠C ?
v) How many pairs of adjacent angles are there? What are they?
vi) How many pairs of opposite angles are there? What are they?

Solution:
In the given quadrilateral ABCD,
i) It has four sides. They are \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CD}} \text { and } \overline{\mathrm{AD}}\)
ii) Opposite side of \(\overline{\mathrm{AB}}\) is \(\overline{\mathrm{DC}}\)
iii) Opposite vertex to B is D.
iv) Opposite angle of ∠C is ∠BAD (or) ∠A.
v) It has four pair of adjacent angles are there. They are :
Adjacent angles of ∠A are ∠B and ∠D.
Adjacent angles of ∠B are ∠A and ∠C.
Adjacent angles of ∠C are ∠B and ∠D.
Adjacent angles of ∠D are ∠A and ∠C.
vi) It has two pairs of opposite angles are there. They are ∠A and ∠C; ∠B and ∠D.

Question 2.
Find the number of lines of symmetry in the following.

Solution:
i) Given adjacent figure is a square.
Number of lines of symmetry to a square are 4

ii) Given adjacent figure is a circle.
Number of lines of symmetry to a circle are infinite (many).

iii) Given adjacent figure is a triangle.
Number of lines of symmetry to the triangle are three.
(If it is an equilateral triangle).

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 9 2D-3D Shapes Ex 9.2 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 9th Lesson 2D-3D Shapes Ex 9.2

Question 1.
Look at the given triangle and answer the following questions.
i) Which points are marked in the exterior of the triangle?
ii) Which points are marked on the triangle?
iii) Which points are marked in the interior of the triangle?

Solution:
i) The points marked in the exterior of the triangle are X, Y and Z.
ii) The points marked on the triangle are A, I, B, J and C.
iii) The points marked in the interior of the triangle are K, L and O.

Question 2.
Look at the adjacent figure. Answer the following questions.
i) How many sides are there in the triangle? What are they?
ii) How many vertices lie there on the triangle? What are they?
iii) What is the side opposite to the vertex P?
iv) What is the vertex opposite to \(\overline{\mathrm{PR}}\) ?

Solution:
In the given ∆PQR,
i) It has three sides. They are \(\overline{\mathrm{PQ}}, \overline{\mathrm{QR}}\) and \(\overline{\mathrm{PR}}\)
ii) It has three vertices. They are P, Q and R.
iii) The side opposite to the vertex P is \(\overline{\mathrm{QR}}
iv) The vertex opposite to the side [latex]\overline{\mathrm{PR}}\) is Q.

Question 3.
Look at the given triangle and answer the following questions.
i) How many angles are there in the triangle? What are they?
ii) What is the angle opposite to \(\overline{\mathrm{MN}}\) ?
iii) Where is the right angle in the given triangle ?

Solution:
In the given ∆MON,
i) It has three angles, they are ∠MNO, ∠NOM and ∠OMN.
ii) Angle opposite to the side \(\overline{\mathrm{MN}}\) is ∠MON or ∠O.
iii) In the triangle ∠MON is the right angle.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 9 2D-3D Shapes Ex 9.1 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 9th Lesson 2D-3D Shapes Ex 9.1

Question 1.
What is the name of four sided polygon? Draw the rough sketch.
Solution:
A four sided polygon is called a quadrilateral.

ABCD is a quadrilateral.

Question 2.
Draw a rough sketch of pentagon.
Solution:
A five sided polygon is called a pentagon.
So, pentagon has five sided figure.

ABCDE is a pentagon.

Question 3.
Write all the sides of the given polygon ABCDEF.
Solution:
Given polygon ABCDEF is a Hexagon.
Its six sides are \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CD}}, \overline{\mathrm{DE}}, \overline{\mathrm{EF}} \text { and } \overline{\mathrm{FA}}\)
So, it is called a Hexagon.

Question 4.
Write the interior angles of the polygon PQRST.
Solution:
Given the polygon PQRST has five sides.
So, it is called a Pentagon.
It has five interior angles.
They are ∠TPQ, ∠PQR, ∠QRS, ∠RST and ∠STP.
They can also be written as ∠P, ∠Q, ∠R, ∠S, ∠T.

Question 5.
Measure the length of the sides of the polygon PQRST.
Solution:
The given polygon has five sides.
They are \(\overline{\mathrm{PQ}}\) = 2cm; \(\overline{\mathrm{QR}}\) = 2.5 cm;
\(\overline{\mathrm{RS}}\) .= 2.4 cm; \(\overline{\mathrm{ST}}\) = 2.2 cm, \(\overline{\mathrm{PT}}\) = 2.5 cm
It’s a pentagon.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 8 Basic Geometric Concepts Unit Exercise Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 8th Lesson Basic Geometric Concepts Unit Exercise

Question 1.
In the given figure, measure the length of AC. Check whether
i) AB + AC > AC
ii) AC > AD – DC
Solution:
In the given figure, AB = 4.2 cm; BC = 5.5 cm
AC = 5.4 cm; CD = 3 cm; AD = 4 cm.
i) AB + AC = 4.2 + 5.4 = 9.6 cm > 5.4 cm
AB + AC > AC
ii) AD – DC = 4 – 3 = 1 cm < 5.4 cm
AD – DC < AC (or) AC > AD – DC

Question 2.
Draw a line segment \(\overline{\mathbf{A B}}\). Put a point C in between \(\overline{\mathbf{A B}}\). Extend \(\overline{\mathbf{C B}}\) upio D such that CD > AB. Now check whether AC and BD are equal length.
Solution:

Let draw a line \(\overline{\mathbf{A B}}\) = 5 cm and mark a point C on \(\overline{\mathbf{A B}}\) such that \(\overline{\mathbf{A C}}\) = 3 cm (or) \(\overline{\mathbf{BC}}\) = 2 cm Extend \(\overline{\mathbf{C B}}\) up to D such that \(\overline{\mathbf{C D}}\) = 5 cm (\(\overline{\mathbf{C B}}\) = 2 cm, \(\overline{\mathbf{B D}}\) = 3 cm)
∴ \(\overline{\mathbf{A C}}\) = 3cm, \(\overline{\mathbf{C B}}\) = 2cm, \(\overline{\mathbf{B D}}\) = 3cm
∴ \(\overline{\mathrm{AC}}=\overline{\mathrm{BD}}\) = 3cm.

Question 3.
Draw an angle ∠AOB as m∠AOB = 40°. Draw an angle ∠BOC such that ∠AOC = 90°
Check whether m∠AOB + m∠BOC = m∠AOC.
Sol. Draw an angle ∠AOB = 40° and ∠AOC = 90° on the same ray \(\overrightarrow{\mathrm{OA}}\)
Now, measure ∠AOB = 40° and ∠BOC = 50°
∴ m∠AOB + m∠BOC = 40° + 50 = 90°
m∠AOB + m∠BOC = 90° = m∠AOC
∴ m∠AOB + m∠BOC = m∠AOC.

Question 4.
Draw an angle ∠XYZ as m∠XYZ = 62°. Measure the exterior angle ∠XYZ.
Solution:

Draw angle ∠XYZ = 62° (Interior)
Now, measure the exterior angle ∠XYZ.
∴ Exterior angle of ∠XYZ = 298°

Question 5.
Match the following.
1. Set square — A) to measure angles
2. Protractor — B) to measure the lengths of line segments
3. Divider — C) to draw parallel lines
Sol. 1) Set square — C) to draw parallel lines
2) Protractor — A) to measure angles
3) Divider — B) to measure the lengths of line segments

Question 6.
List out the letters of English alphabet (capital letters) which consist of right angles.
Solution:
The letters which consists of right angles in English alphabet are

Question 7.
Measure the angles ∠AQP, ∠CPR, ∠BRQ.

Find m∠AQP, m∠CPR, m∠BRQ.
Solution:
In the given figure, measure the angles ∠AQR, ∠CPR, ∠BRQ
∠AQP = 120°
∠CPR = 120°
and ∠BRQ = 120°
∴ m∠AQP = 120°; m∠CPR = 120°; m∠BRQ = 120°

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 8 Basic Geometric Concepts Ex 8.4 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 8th Lesson Basic Geometric Concepts Ex 8.4

Question 1.

Measure all the angles in the above figures.

∠1 = 70°
∠3 = 70°
∠5 = 70°
∠7 = 70°

∠2 = 110°
∠4 = 110°
∠6 = 110°
∠8= 110°

∠a = 60°
∠c = 60°
∠e = 50°
∠g = 50°

∠b = 120°
∠d = 120°
∠f = 130°
∠h = 130°

Question 2.
Sum of which two angles is 180° in each figure ?
Solution:
From above question,
i) ∠1 + ∠2 = 180°

i) ∠1 + ∠2 = 180°
∠2 + ∠3 = 180°
∠1 + ∠4 = 180°
∠3 + ∠4 = 180°

∠5 + ∠6 = 180°
∠6 + ∠7 = 180°
∠7 + ∠8 = 180°
∠5 + ∠8 = 180°

∠1 + ∠8 = 180°
∠4 + ∠5 = 180°
∠2 + ∠7 = 180°
∠3 + ∠6 = 180°

ii) ∠a + ∠b = 180°
∠b + ∠c = 180°
∠c + ∠d = 180°
∠a + ∠d = 180°

∠e + ∠f = 180°
∠f + ∠g = 180°
∠g + ∠h = 180°
∠e + ∠h = 180°

Question 3.
In the given figure measure ∠FOG and draw the same in your note book.

Solution:

Question 4.
In the given figure measure the angles ∠AOB, ∠BOC.

Solution:

∠AOB = 110°
∠BOC = 60°
∠AOC = 50°

Question 5.
Write some acute, obtuse and reflexive angles atleast 2 for each.
Solution:
Acute angles : 10°, 30°, 45°, 60°, 89° (< 90°)
Obtuse angles : 110°, 150°, 160°, 172°, 178° (90° < obtuse < 180°) Reflex angles : 210°, 270°, 300°, 345°, 359° (reflex > 180°)

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 8 Basic Geometric Concepts Ex 8.3 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 8th Lesson Basic Geometric Concepts Ex 8.3

Question 1.
Given ” \(\overline{\mathrm{AB}} / / \overline{\mathrm{CD}}\), l ⊥ m”. Which are perpendicular? Which are parallel?
Solution:
are parallel lines (// is the symbol for parallel),
l, m are perpendicular lines (⊥ is the symbol for perpendicular).

Question 2.
Write the set of parallels and perpendiculars in the given by using symbols.

Solution:
a) \(\overline{\mathrm{AB}}, \overline{\mathrm{DC}}\) are parallel lines, we denote this by writing \(\overline{\mathrm{AB}} / / \overline{\mathrm{DC}}\) and can be read as \(\overline{\mathrm{AB}}\) is parallel to \(\overline{\mathrm{DC}}\)
b) \(\overline{\mathrm{AD}}, \overline{\mathrm{BC}}\) are parallel lines. We denote this by writing \(\overline{\mathrm{AD}} / / \overline{\mathrm{BC}}\) and can be read as \(\overline{\mathrm{AD}}\) is parallel to \(\overline{\mathrm{BC}}\)
c) \(\overline{\mathrm{AQ}}, \overline{\mathrm{PC}}\) are parallel lines. We denote this by writing \(\overline{\mathrm{AQ}} / / \overline{\mathrm{PC}}\) and can be read as \(\overline{\mathrm{AQ}}\) is parallel to \(\overline{\mathrm{PC}}\).
d) \(\overline{\mathrm{AB}}, \overline{\mathrm{AD}}\) are perpendicular lines. We denote this by writing \(\overline{\mathrm{AB}} \perp \overline{\mathrm{AD}}\) and can be read as \(\overline{\mathrm{AB}}\) is perpendicular to \(\overline{\mathrm{AD}}\).
e) \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}\) are perpendicular lines. We denote this by writing \(\overline{\mathrm{AB}} \perp \overline{\mathrm{BC}}\) and can be read as \(\overline{\mathrm{AB}}[latex] is perpendicular to [latex]\overline{\mathrm{BC}}\) .
f) \(\overline{\mathrm{BC}}, \overline{\mathrm{CD}}\) are perpendicular lines, we denote this by writing \(\overline{\mathrm{BC}} \perp \overline{\mathrm{CD}}\) and can be read as \(\overline{\mathrm{BC}}\) is perpendicular to \(\overline{\mathrm{CD}}\).
g) \(\overline{\mathrm{CD}}, \overline{\mathrm{AD}}\) are perpendicular lines, we denote this by writing \(\overline{\mathrm{CD}} \perp \overline{\mathrm{AD}}\) and can be read as \(\overline{\mathrm{CD}}\) is perpendicular to \(\overline{\mathrm{AD}}\).

ii) \(\overline{\mathrm{PX}}, \overline{\mathrm{QR}}\) are perpendicular lines, we denote this by writing \(\overline{\mathrm{PX}} \perp \overline{\mathrm{QR}}\) and can be read as \(\overline{\mathrm{PX}}\) is perpendicular to \(\overline{\mathrm{QR}}\).

iii) a) \(\overline{\mathrm{LM}}, \overline{\mathrm{KN}}\) are parallel lines. We denote this by writing \(\overline{\mathrm{LM}} / / \overline{\mathrm{KN}}\) and can be read as \(\overline{\mathrm{LM}}\) is parallel to \(\overline{\mathrm{KN}}\).
b) \(\overline{\mathrm{MN}}, \overline{\mathrm{LK}}\) are parallel lines. We denote this by writing \(\overline{\mathrm{MN}} / / \overline{\mathrm{LK}}\) and can be read as \(\overline{\mathrm{MN}}\) is parallel to \(\overline{\mathrm{LK}}\).
c) \(\overline{\mathrm{ON}}, \overline{\mathrm{LP}}\) are parallel lines. We denote this by writing \(\overline{\mathrm{ON}} / / \overline{\mathrm{LP}}\) and can be read
as \(\overline{\mathrm{ON}}\) is parallel to \(\overline{\mathrm{LP}}\)
d) \(\overline{\mathrm{LM}}, \overline{\mathrm{ON}}\) are perpendicular lines, we denote this by writing \(\overline{\mathrm{ON}} \perp \overline{\mathrm{LM}}\) and can be read as \(\overline{\mathrm{ON}}\) is perpendicular to \(\overline{\mathrm{LM}}\).
e) \(\overline{\mathrm{LP}}, \overline{\mathrm{KN}}\) are perpendicular lines, we denote this by writing \(\overline{\mathrm{LP}} \perp \overline{\mathrm{KN}}\) and can be read as \(\overline{\mathrm{LP}}\) is perpendicular to \(\overline{\mathrm{KN}}\).

Question 3.
From the given figure find out the Intersecting lines and concurrent lines.

Solution:
i) Intersecting lines : (l, m); (l, n); (n, o); (m, o); (l, o); (m, n)
ii) Intersecting lines: (p, q); (p, r); (p, s); (q, r); (q, s)
Concurrent lines : (p, q, s)

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 11 Perimeter and Area Ex 11.2 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 11th Lesson Perimeter and Area Ex 11.2

Question 1.
Find the circumferences of the circles with the radius given below.
A) 7 cm B) 3.5 cm C) 14 cm
Solution:
A) Given radius (r) = 7 cm
Circumference of a circle C = 2πr (∵ π = \(\frac{22}{7}\))
= 2 x \(\frac{22}{7}\) x 7 = 44 cm
∴ Circumference of a circle = 44 cm ‘

B) Given radius (r) = 3.5 cm
Circumference of a circle C = 2πr (∵ π = \(\frac{22}{7}\))
= 2 x \(\frac{22}{7}\) x 3.5
∴ Circumference of a circle = 22 cm

C) Given radius (r) = 14 cm
Circumference of a circle C = 2πr (∵ π = \(\frac{22}{7}\))
= 2 x \(\frac{22}{7}\) x 14
∴ Circumference of a circle = 88 cm

Question 2.
Given below are the circumferences of different circles. Find the radius of each circle.
A) 4.4 m B) 176 cm C) 1.54 cm
Solution:
A) Given circumference of a circle = 2πr = 4.4 m
2 x \(\frac{22}{7}\) x r = 4.4
Divide with 2 x \(\frac{22}{7}\) on both sides.

∴ Radius of the circle (r) = 0.7 m = 70 cm.

B) Given circumference of a circle = 2πr =176 cm
2 x \(\frac{22}{7}\) x r = 176
Divide with 2 x \(\frac{22}{7}\) on both sides.

∴ Radius of the circle (r) = 28 cm.

C) Given circumference of a circle is C = 2πr = 1.54 cm
2 x \(\frac{22}{7}\) x r = 1.54
Divide with 2 x \(\frac{22}{7}\) on both sides.

∴ Radius of the circle (r) = 0.245 cm

Question 3.
A gold smith has 8.8m of gold wire with him. He has to make gold rings of 2cm radius. How many such rings he can make with it?
Solution:
Given the radius of the gold ring r = 2 cm
Length of the gold wire = 8.8 m (or) = 880 cm
To find the? number of rings we have to divide the length of the gold wire by circumference of the gold ring.
Now, circumference of the gold ring C = 2πr

Number of rings made by gold smith = 70

Question 4.
A wire was bent in the shape of a circle with radius 7cm. If the same wire was again used to make a square, then find its side.
Solution:
Given radius of the circle r = 7 cm
Circumference of the circle C = 2πr
= 2 x \(\frac{22}{7}\) x 7 = 44 cm
Given length of the wire same.
So, perimeter of square = circumference of the circle
4 x side = 44 cm
Divide with 4 on both sides = \(\frac{4 \times \text { side }}{4}=\frac{44}{4}\)
Side = 11 cm
∴ Side of square = 11cm.

Question 5.
In a chemical factory two wheels of different radius were connected with a belt. Radius of the bigger wheel is 21cm and radius of the smaller wheel is 7cm. If the bigger wheel rotates completely 100 times, find out the number of times that the smaller wheel rotates. .
Solution:
Given the radius of the bigger wheel R = 21 cm
Circumference of the bigger wheel C = 2πR = 2 x \(\frac{22}{7}\) x 21 = 132 cm
If the bigger wheel completes 100 rotations,
Distance covered by the bigger wheel = Number of rotates x circumference
= 100 x 132 = 13,200 cm
Now, radius of smaller wheel r = 7 cm.
Circumference of the smaller wheel C = 2πr = 2 x \(\frac{22}{7}\) x 7 = 44cm
If the smaller wheel completes ‘n’ rotations,
Distance covered by the smaller wheel = number of rotations x circumference
= n x 44 = 44n cm
Distance covered by the small wheel = Distance covered by the bigger wheel
44n = 13200 cm
Divide with 44 as both sides,
\(\frac{44 n}{44}=\frac{13200}{44}\) = 300
n = 300
∴ Number of rotations made by the smaller wheel = 300.

Question 6.
Mohan is playing with a ring of diameter 14 cm, which is made up of metallic wire. When his brother asked, Mohan stretched the wire and made it as two equal parts. With those parts, he made another two small rings. Find the radius of smaller ring. Sol. Given the diameter of the bigger ring
Solution:
Given the diameter of the bigger ring = 14 cm
Radius of the bigger ring R = \(\frac{\text { diameter }}{2}\)
R = \(\frac{14}{2}\) = 7 cm
Length of the wire = Circumference of the bigger ring
= 2πR = 2 x \(\frac{22}{7}\) x 7 = 44 cm
If Mohan stretched the wire into’ halves.
Then the length of half of the wire = circumference of the bigger ring ÷ 2
= \(\frac{44}{2}\) = 22 cm
Circumference of the smaller ring = 2πr = 22
2 x \(\frac{22}{7}\) x r = 22
Divide with 2 x \(\frac{22}{7}\) on both sides

∴ Radius of the smaller ring = 3.5 cm

Question 7.
In designing an iron gril a black smith needed 70 rings with radius of 7cm each. Find how much length of the rod he required, if the wastage is 20 cm.
Solution:
Given radius of the ring r = 7 cm
Circumference of the ring C = 2πr = 2 x \(\frac{22}{7}\) x 7 = 44 cm
Length of rod required to make one ring = 44 cm
Length of rod required to make 70 rings = 44 x 70 = 3080 cm
Wastage = 20 cm
Required length of rod to make 70 rings = 3080 + 20 = 3100 c

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 11 Perimeter and Area Ex 11.1 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 11th Lesson Perimeter and Area Ex 11.1

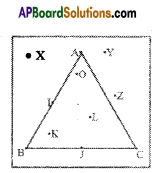
Question 1.
Find the perimeters of the following figures.

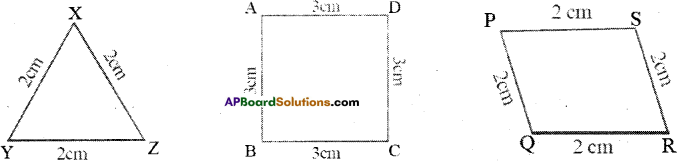
i) Check whether the perimeter of Δ XYZ = 3 x Length of the side?
ii) Check whether the perimeter of □ ABCD = 4 x Length of the side?
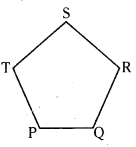
iii) Check whether the perimeter of □ PQRS = 4 x Length of the side?
i) In ΔXYZ, XY = 2cm, YZ = 2cm and XZ = 2cm
Perimeter of ΔXYZ = XY + YZ + XZ = 2 + 2 + 2 = 6cm
Perimeter of ΔXYZ = 6 cm
By observing that perimeter of ΔXYZ = 6cm = 3 x 2cm
= 3 x length of the side in ΔABC
So, perimeter of ΔXYZ = 3 x length of the side

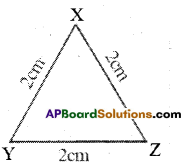
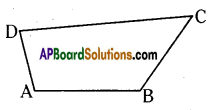
ii) Given in quadrilateral ABCD, AB = 3cm, BC = 3cm, CD = 3cm and AD
Perimeter of □ ABCD = AB + BC + CD + AD = 3 + 3 + 3 + 3
Perimeter of □ ABCD = 12 cm
By observing that perimeter of □ ABCD = 12cm = 4 x 3cm
= 4 x length of the side in □ ABCD
So, perimeter of □ ABCD = 4 x length of the side

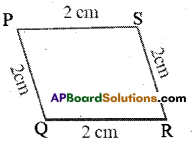
iii)In quadrilateral PQRS, .
Given PQ = 2cm, QR = 2cm, RS = 2cm and PS = 2cm
Perimeter of PQRS = PQ + QR + RS + PS = 2 + 2 + 2 + 2 = 8cm
Perimeter of PQRS = 8cm.
By observing that perimeter of PQRS = 8cm = 4×2 cm
= 4 x length of the side in PQRS
So, perimeter of PQRS = 4 x length of the side.

Question 2.
Measurements of two rectangular fields are 50m x 30m and 60m x 40m. Find their perimeters. Check whether the perimeters are 2 x length + 2 x breadth.
Solution:

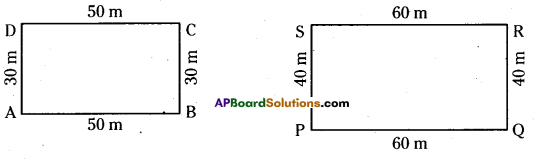
Given, in rectangle ABCD, AB = DC = 50 m and BC = DA = 30 m
Perimeter of rectangle ABCD = AB + BC + CD + DA
= 50 + 30 + 50 + 30
= 2 x 50 + 2x 30 = 160 m
∴ Perimeter of rectangle ABCD = 2 x length + 2 x breadth
Given in rectangle PQRS, PQ = RS = 60 m and QR = SP = 40 m
Perimeter of rectangle PQRS = PQ + QR + RS + SP
= 60 + 40 + 60 + 40
= 2 x 60 + 2 x 40 = 200 m
∴ Perimeter of rectangle PQRS = 2 x length + 2 x breadth

Question 3.
Find the perimeter of
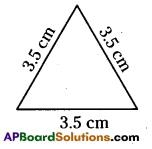
a) An equilateral triangle whose side is 3.5cm.
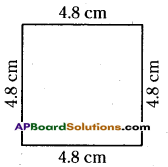
b) A square whose side is 4.8cm.
Solution:
a) Given side of an equilateral triangle is 3.5 cm.
We know that, perimeter of an equilateral triangle
= 3 x length of the side = 3 x 3.5 = 10.5 cm .
∴ Perimeter = 10.5 cm

b) Given side of a square = 4.8 cm
We know that, perimeter of a square
= 4 x length of the side 4 x 4.8
∴ Perimeter = 19.2 cm

Question 4.
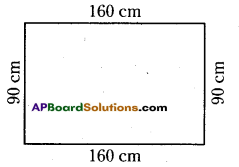
Length and breadth of top of one table is 160cm and 90cm respectively. Find how . much length of beading is required for each table.
Solution:
Given the length of top of table =160 cm
breadth of top of table = 90 cm g
To find the length of beading we have to find the ®
perimeter of the table top. .
So, perimeter of table top = 160 + 90 + 160 + 90 = 500 cm 160 cm
Required length of beading of table top = 500 cm.

Question 5.
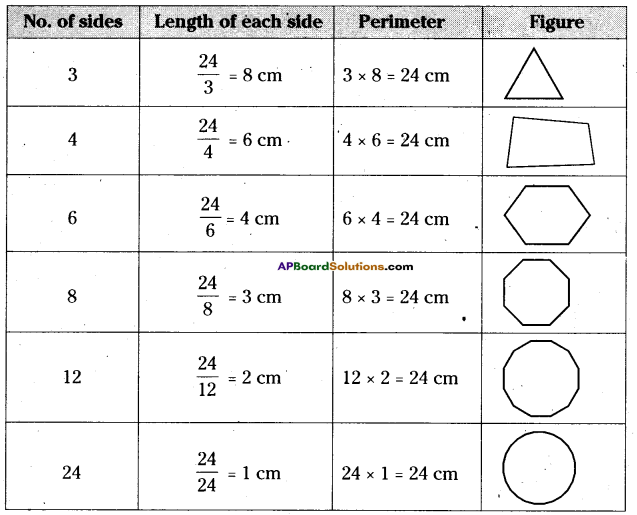
Manasa has 24cm of metallic wire with her. She wanted to make some polygons with equal sides whose sides are integral without milling into pieces values. Find how many such polygons she can make with the length of 24cm metallic wire?
Solution:
Given length of metallic wire = 24 cm
We know that 24 = 1 x 24
= 2 x 12
= 3 x 8
= 4 x 6
∴ 24 can be divided into 1,2,3,4,6,8,12 & 24
But we can’t form polygons with sides 1 & 2.
∴ The polygons with sides 3, 4, 6, 8, 12 and 24 can be formed.
The length of the sides are equal so \(\) and \(\) units.
They are 8 cm, 6cm, 4cm, 3cm, 2cm and 1cm respectively

Question 6.
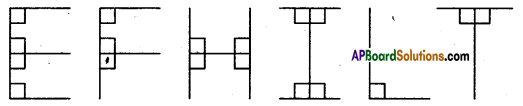
Find the perimeter of the following figures. (i) and (ii)

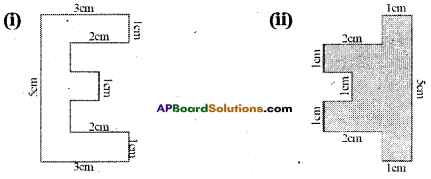
i) Perimeter of the given polygon is sum of the lengths of its all sides.
Perimeter = 5cm + 3cm+ 1cm + 2cm + 1 cm + 1 cm + 1 cm + 1 cm + 1cm + 2cm + 1 cm + 3cm
Perimeter = 22 cm

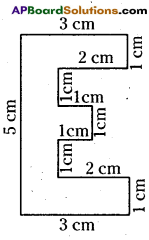
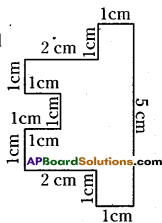
ii) Perimeter of the given polygon is sum of the lengths of its all sides.
Perimeter = 1cm + 5cm + 1 cm + lcm+ 2cm + 1cm + 1cm + 1cm + 1cm + 1cm + 2cm + 1cm
Perimeter = 18cm

Question 7.
Statement P : So many rectangles exists with the same perimeter.
Statement Q : So many squares exists with the same perimeter.
Which option is correct?
A) P wrong Q correct
B) P correct Q wrong
C) P and Q are correct
D) P and Q are wrong
Solution:
B) P correct Q wrong.
Lengths and breadths of a rectangle can change for the same perimeter. But, the side of a square cannot change for the same perimeter.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 10 Practical Geometry Unit Exercise Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 10th Lesson Practical Geometry Unit Exercise

Question 1.
Construct a circle with centre X and diameter 10 cm. Sol. Given diameter of circle d = 10 cm
Solution:
We know that radius of circle r = \(\frac{d}{2}=\frac{10}{2}\) = 5
So, radius of the circle is 5 cm.
Now, draw a circle with radius 5 cm.

Question 2.
Draw four circles of radius 2 cm, 3 cm, 4 cm and 5 cm with the same centre P.

Solution:
Radii of four circles are PA = 2cm, PB = 3cm, PC = 4cm and PD = 5cm with the same centre P was constructed.

Question 3.
Draw the angles given below using a protractor.
(i) 75°
(ii) 15°
(iii) 105°
Solution:
(i) 75°

∠ADI = 75°
Steps of construction :

1. Draw a ray \(\overrightarrow{\mathrm{DI}}\) with vertex D.
2. Place the centre point of the protractor at D and the line be aligned with DI.
3. Mark a point A at 75°.
4. Join DA. ∠ADI = 75° is formed.
   Hence the required angle ∠ADI = 75° is constructed.

ii) 15°

∠KIS = 15°
Steps of construction:

1. Draw a ray \(\overrightarrow{\mathrm{IS}}\) with vertex I.
2. Place the centre point of the protractor at I and the line be aligned with \(\overrightarrow{\mathrm{IS}}\).
3. Mark a point K at 15°.
4. Join IK.∠KIS = 15° is formed.
   Hence the required angle ∠KIS = 15° is constructed.

(iii) 105°

∠MAD = 105°
Steps of construction:

1. Draw a ray \(\overrightarrow{\mathrm{AD}}\) with initial point A.
2. Place the centre point of the protractor
   at A and the line be aligned with \(\overrightarrow{\mathrm{AD}}\).
3. Mark a point M at 105°.
4. Join AM.∠MAD = 105° is formed.
   Hence the required angle∠MAD = 105° ¡s constructed.

Question 4.
Construct ∠ABC = 50° and then draw another angle ∠XYZ equal to ∠ABC without using a protractor.
Solution:

Given ∠ABC = 50° and ∠XYZ = 50°.
Steps of construction:

1. Construct ∠ABC = 50°by using protractor.
2. By taking any radius draw arcs from B on AB and BC at P and Q respectively.
3. Draw a ray \(\overrightarrow{\mathrm{YX}}\) with initial point Y.
4. By taking BP as radius draw an arc on \(\overrightarrow{\mathrm{YX}}\) from Y which meets at K.
5. Draw arc from Y by taking PQ as radius in the ∠BAC which cuts the previous arc and mark it as L. Now draw \(\overrightarrow{\mathrm{YZ}}\). So, ∠XYZ = 50° is formed.
   Hence ∠XYZ = 50° is constructed which is equal to ∠ABC = 50°.

Question 5.
Construct ∠DEF = 60°. Bisect it, measure each half by using a protractor.
Solution:

Given ∠DEF = 60°
Draw EX as the bisector of ∠DEF.
So, ∠DEX = ∠XEF = \(\frac{\angle \mathrm{DEF}}{2}=\frac{60^{\circ}}{2}\) = 30°
∴ ∠DEX = ∠XEF = 30°

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 10 Practical Geometry Ex 10.4 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 10th Lesson Practical Geometry Ex 10.4

Question 1.
Construct ∠ABC = 60° without using protractor.
Solution:
Steps of construction :

1. Draw a line l and mark a point B on it.
2. Place the pointer of the compasses at B and draw an arc of convenient radius which cuts the line l at a point C.
3. With the pointer at C as centre and with the same radius as above. Now draw an arc that passes through B.
4. Cut intersecting point of two arcs is A. Join BA. ∠ABC = 60° is formed.
   Hence the required angle ∠ABC = 60° is constructed.
   

Question 2.
Construct an angle of 120° with using protractor and compasses.
Solution:
Steps of construction :

1. Draw a ray \(\overline{\mathrm{OA}}\) of any length.
2. Place the pointer of the compasses at O. With O as centre and any convenient radius draw an arc cutting OA at M.
3. With M as centre and without altering radius draw an arc which cuts the previous arc at P.
4. With P as centre and without changing radius draw an arc which cuts the first arc at Q.
5. Join OQ. Then ∠AOQ is the required angle.
   Hence the required angle ∠AOQ = 120° is constructed.
   

Question 3.
Construct the following angles using ruler and compasses. Write the steps of construction in each case.
i) 75°
ii) 15°
iii) 105°
Solution:
i) 75°
Steps of construction:

1. Construct ∠RAM 900
2. Construct ∠PAM = 600 AM as common arm
3. Now, ∠PAR = ∠RAM – ∠PAM = 90° – 60° = 30°
4. Draw bisector to ∠PAR which is \(\overrightarrow{\mathrm{AQ}}\).
5. Now, ∠MAQ = ∠PAM + ∠PAQ = 60° + \(\frac{30^{\circ}}{2}\)
   = 60° + 15° = 75° (QED)
   

ii) 15°
Steps of construction:

1. Construct ∠BQR = 60°
2. Draw the bisector to ∠BQR which is \(\overrightarrow{\mathrm{QC}}\)
3. Now,∠CQR = \(\frac{60^{\circ}}{2}\) = 30°
4. Draw the bisector \(\overrightarrow{\mathrm{QP}}\) to∠CQR.
5. ∠PQR = \(\frac{1}{2}\) x 30° = 15° (Q.E.D)
   

iii) 105°
Steps of construction :

1. Construct ∠IDS = 90°
2. Construct ∠ADS = \(\frac{\angle \mathrm{RDS}}{2}=\frac{30^{\circ}}{2}\) = 15°
3. Now, ∠ADI = ∠IDS + ∠ADS = 90° + 15°
   ∴ ∠ADI = 105° (Q.E.D)