SCERT AP 10th Class Maths Textbook Solutions Chapter 4 రెండు చరరాశులలో రేఖీయ సమీకరణాల జత Exercise 4.2 Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 4th Lesson రెండు చరరాశులలో రేఖీయ సమీకరణాల జత Exercise 4.2
క్రింది సమస్యలలో ప్రతి సందర్భంలో రేఖీయ సమీకరణాల జతను వ్రాసి దానికి సాధన కనుగొనండి.
ప్రశ్న 1.
ఇద్దరు వ్యక్తుల ఆదాయాల నిష్పత్తి 9 : 7 మరియు వాటి ఖర్చుల నిష్పత్తి 4 : 3. వారు ప్రతీ ఒక్కరూ నెలకు ₹ 2000 సొమ్ము ఆదాచేసిన, వారి నెలవారీ ఆదాయాలను కనుగొనండి.
సాధన.
ఇద్దరు వ్యక్తుల ఆదాయాల నిష్పత్తి = 9 : 7.
మొదటి వ్యక్తి ఆదాయం = ₹ 9x
రెండవ వ్యక్తి ఆదాయం = ₹ 7x అనుకొనుము
వారి ఖర్చుల నిష్పత్తి = 4 : 3
మొదటి వ్యక్తి ఖర్చు = ₹ 4y
రెండవ వ్యక్తి ఖర్చు = ₹ 3y అనుకుందాము.
ప్రతీ ఒక్కరూ నెలకు ఆదా చేస్తున్న సొమ్ము = ₹ 2000
మొదటి వ్యక్తి ఆదా చేస్తున్న సొమ్ము
9x – 4y = 2000 ……… (1)
రెండవ వ్యక్తి ఆదా చేస్తున్న సొమ్ము
7x – 3y = .2000 ………. (2)
1వ పద్ధతి (చరరాశి తొలగింపు పద్ధతి) :

∴ x = 2000
మొదటి వ్యక్తి ఆదాయం = 9x = 9 × 2000 = ₹ 18000
రెండవ వ్యక్తి ఆదాయం = 7x = 7 × 2000 = ₹ 14000.
![]()
రెండవ పద్ధతి (ప్రతిక్షేపణ పద్ధతి) :
(1) ⇒ – 4y = 2000 – 9x
4y = 9x – 2000
y = \(\frac{9 x-2000}{4}\) ను (2) లో ప్రతిక్షేపించగా.
7x – 3(\(\frac{9 x-2000}{4}\)) = 2000
\(\frac{28 x-27 x+6000}{4}\) = 2000
x + 6000 = 8000
x = 8000 – 6000 = 2000
మొదటి వ్యక్తి ఆదాయం = 9x = 9 × 2000 = ₹ 18000
రెండవ వ్యక్తి ఆదాయం = 7x = 7 × 2000 = ₹ 14000
సరిచూసుకోవడం :
ఆదాయాల నిష్పత్తి = 18000 : 14000 = 9 : 7
ఖర్చుల నిష్పత్తి = 18000 – 2000 : 14000 – 2000
16000 : 12000 = 4 : 3.
![]()
ప్రశ్న 2.
ఒక రెండంకెల సంఖ్య మరియు దానిలోని స్థానాలను, తారుమారు చేయగా వచ్చిన సంఖ్యల మొత్తము 66. ఆ సంఖ్యలోని రెండు అంకెల భేదము 2 అయిన ఆ సంఖ్యను కనుగొనుము. అటువంటి సంఖ్యలు ఎన్ని ఉంటాయి ?
సాధన.
ఒకట్ల స్థానంలోని అంకె = x
పదుల స్థానంలోని అంకె = y అనుకొందాం.
రెండంకెల సంఖ్య = 10x + y
అంకెలను తారుమారు చేయగా
ఒకట్ల స్థానంలోని అంకె = y
పదుల స్థానంలోని అంకె = x
రెండంకెల సంఖ్య = 10y + x
లెక్క ప్రకారం, ఒక రెండంకెల సంఖ్య మరియు దానిలోని స్థానాలను మార్పు చేయగా వచ్చిన సంఖ్యల మొత్తం
∴ (10x + y) + (10y +x) = 66.
⇒ 11x + 11y = 66
x + y = 6 ……….. (1)
అలాగే ఆ సంఖ్యలోని రెండంకెల భేదము
x – y = 2 ……… (2) లేదా
y – x = 2 ……….. (3)
(1) & (2) ల నుండి
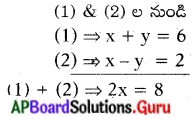
x = \(\frac{8}{2}\) = 4
x = 4 ను (1) లో రాయగా
4 + y = 6
y = 6 – 4 = 2
సాధన x = 4, y = 2
కావలసిన సంఖ్య = 42
(1) & (3) ల నుండి .
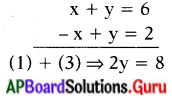
y = \(\frac{8}{2}\) = 4
y = 4 ను (1) లో రాయగా
x + 4 = 6
x = 6 – 4 = 2
సాధన y = 2, y = 4
కావలసిన సంఖ్య = 24
∴ ఇచ్చిన షరతులను పాటించేటట్లు 24 మరియు 42 అనే రెండు సంఖ్యలు ఉంటాయి.
![]()
ప్రశ్న 3.
రెండు సంపూరక కోణాలలో పెద్ద కోణము, చిన్న కోణము కన్నా 18° ఎక్కువ. అయిన ఆ కోణాలను కనుగొనండి.
సాధన.
పెద్ద కోణము = x;
చిన్న కోణము = y అనుకుందాము.
పై రెండు కోణాలు .సంపూరకాలు.
x + y = 180° ……. (1)
పెద్ద కోణము, చిన్న కోణము కన్నా 18° ఎక్కువ.
x = y + 18° ……. (2)
(2) ని (1) లో ప్రతిక్షేపించగా,
y + 18° + y = 180°
2y = 180° – 18° = 162°
y = \(\frac{162}{2}\) = 81°
y = 81°ను (2) లో ప్రతిక్షేపించగా, x = 81° + 18° = 99°
సాధన x = 99°, y = 81°
∴ పెద్ద కోణము = 99°; చిన్న కోణము = 81°
2వ పద్ధతి (చరరాశి తొలగింపు పద్ధతి) :
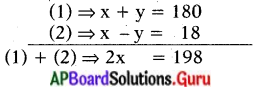
x = \(\frac{198}{2}\) = 99°
x = 99 ను (1) లో రాయగా,
99 + y = 180° ⇒ y = 180 – 99 = 81°
సాధన x = 99, y = 81
∴ పెద్ద కోణము = 999; చిన్న కోణము = 81°
సరి చూసుకోవడం :
x, y విలువలను (1) లో ప్రతిక్షేపించగా, 99° + 81° = 180° (సంపూరకాలు)
99° = 81° + 18°.
![]()
ప్రశ్న 4.
హైదరాబాద్ లో టాక్సీ ఛార్జీలు రెండు అంశాలుగా ఉంటాయి. మొదటిది స్థిర ఛార్జీ కాగా, రెండవది దూరాన్ని బట్టి నిర్ణయించే ఛార్జీ. 10కి.మీ. దూరం ప్రయాణం చేసినపుడు అయిన మొత్తము ఛార్జి ₹ 220. అలాగే 16 కి.మీ. దూరం ప్రయాణం చేసినపుడు అయిన మొత్తము ఛార్జి ₹ 310. అయిన
(i) స్థిర ఛార్జీ విలువ మరియు ఒక కిలోమీటరుకు అయ్యే ఛార్జీల విలువ ఎంత ?
(ii) ఒక వ్యక్తి 25 కి.మీ. దూరం ప్రయాణించిన అతను ఛార్జీల నిమిత్తం చెల్లించవలసిన మొత్తం ఎంత ?
సాధన.
(i) స్థిర ఛార్జీ = ₹ x అనుకొందాం.
కిలోమీటరుకు అయ్యే ఛార్జీ = ₹ y అనుకొందాం.
10 కి.మీ. దూరం ప్రయాణం చేసినపుడు అయిన మొత్తం ఛార్టీ = ₹ 220
x + 10y = 220 ………….. (1)
15 కి.మీ. దూరం ప్రయాణం చేసినపుడు అయిన మొత్తం ఛార్టీ = ₹ 310
x + 15y = 310 …… (2)

y = \(\frac{90}{5}\) = 18
y = 18ని (1) లో రాయగా,
x + 10 (18) = 220
⇒ x + 180 = 220
x = 220 – 180 = ₹ 40
సాధన x = ₹ 40, y = ₹ 18 ,
∴ స్థిర ఛార్జీ = ₹ 40
కిలో మీటరుకు అయ్యే ఛార్జీ = ₹18.
2వ పద్ధతి (ప్రతిక్షేపణ పద్ధతి) :
(1) ⇒ x = 220 – 10y ని (2) లో ప్రతిక్షేపించగా,
220 – 10y + 15y = 310
5y = 310 – 220
5y = 90
y = \(\frac{90}{5}\) = 18
y = 18 ని (1) లో రా యగా,
x + 10 (18) = 220
x + 180 = 220
x = 220 – 180 = ₹ 40
∴ సాధన x = ₹ 40, y = ₹ 18.
∴ స్థిరఛార్టీ = ₹ 40
కిలోమీటరుకు అయ్యే ఛార్జీ = ₹ 18.
సరిచూసుకోవడం :
10 కి.మీ.లకు అయ్యే ఛార్జీ = స్థిర ఛార్జీ + 10 కి.మీ. ఛార్జీ –
40 + 10 × 18 = 40 + 180 = ₹ 220
(ii) 40 + 25 × 18 = 40 + 450 = 490.
![]()
ప్రశ్న 5.
ఒక భిన్నంలో లవ, హారాలకు 1 కలిపిన అది \(\frac{4}{5}\) అవుతుంది. అలాగే లవ, హారాల నుండి 5 తీసివేసిన ఆ భిన్నము 1/2 అవుతుంది. అయిన ఆ భిన్నాన్ని కనుగొనండి..
సాధన.
లవం = x, హారం = y అనుకుందాము.
∴ భిన్నము = \(\frac{x}{y}\)
లవ, హారాలకు 1 కలిపిన ఆ భిన్నం \(\frac{4}{5}\) అవుతుంది.
\(\frac{x+1}{y+1}=\frac{4}{5}\) (అడ్డగుణకారము చేయగా)
5x + 5 = 4y + 4
5x – 4y = 4 – 5
5x – 4y = – 1 ……… (1)
లవ, హారాల నుండి 5 తీసివేసిన 1/2 అవుతుంది.
\(\frac{x-5}{y-5}=\frac{1}{2}\)
∴ 2x – 10 = y – 5,
2x – y = – 5 + 10
2x – y = 5 ………. (2)
(2) ⇒ – y = 5 – 2x ,
y = 2x – 5 ను (1) లో ప్రతిక్షేపించగా,
5x – 4 (2x – 5) = – 1
5x – 8x + 20 = – 1
– 3x = – 1 – 20 = – 21
3x = 21 ⇒ x = \(\frac{21}{3}\) = 7
x = 7 ను (2) లో రాయగా,
2(7) – y = 5 = 14 – y = 5
⇒ y = 5 – 14 = – 9
⇒ y = 9
సాధన, x = 7, y = 9
∴ భిన్నము = \(\frac{7}{9}\)
2వ పద్ధతి (చరరాశి తొలగింపు పద్ధతి) :

3x = 21
⇒ x = \(\frac{21}{3}\) = 7
x = 7 ను (2) లో రాయగా,
2 (7) – y = 5
– y = 5 – 14 = – 9
⇒ y = 9
సాధన x = 7, y = 9
భిన్నము = \(\frac{7}{9}\)
సరిచూచుట :
\(\frac{7+1}{9+1}=\frac{8}{10}=\frac{4}{5}\)
![]()
ప్రశ్న 6.
ఒక రహదారిపై గల A, B అనే ప్రదేశాలు 100 కి.మీ. దూరంలో ఉన్నాయి. A నుండి ఒక కారు, B నుండి ఒక కారు ఒకే సమయంలో వేరు వేరు వేగాలతో ప్రయాణిస్తున్నాయి. ఆ రెండు కార్లు ఒకే దిశలో ప్రయాణం చేసిన అవి 5 గంటల తరువాత కలుస్తాయి. అలాకాక అవి ఒకదానివైపు ఒకటి ప్రయాణం చేసిన 1 గంట తరువాత కలుస్తాయి. అయిన ఆ రెండు కార్ల వేగాలను కనుగొనండి. D
సాధన.
A నుండి బయలుదేరిన కారు వేగం = x కి.మీ./గం.
B నుండి బయలుదేరిన కారు వేగం = y కి.మీ./గం. అనుకుందాం.
రెండు కార్లు. ఒకే దిశలో ప్రయాణం చేసిన అవి 5 గంటల తర్వాత కలుస్తాయి. (x > y)
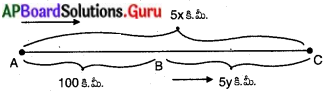
5 గంటలలో 4 నుండి బయలుదేరిన కారు ప్రయాణించిన దూరం = 5x కి.మీ.
5 గంటలలో B నుండి బయలుదేరిన కారు ప్రయాణించిన దూరం = 5y కి.మీ.
∴ 5x = 100 + 5y
5x – 5y = 100
5 (x – y) = 100 x – y = 20 ………… (1)
రెండు కార్లు ఒకదానివైపు ఒకటి ప్రయాణంచిన అవి 1 గంట తరువాత కలుస్తాయి
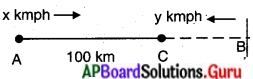
A నుండి బయలుదేరిన కారు 1 గంటలో ప్రయాణించిన దూరం = x కి.మీ.
B నుండి బయలుదేరిన కారు 1 గంటలో ప్రయాణించిన దూరం = y కి.మీ.
∴ x + y = 100 …….. (2)
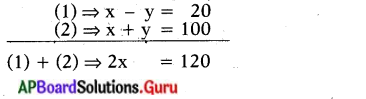
x = \(\frac{120}{2}\) = 60
x = 60ని (2) లో రాయగా,
60 + y = 100
⇒ y = 100 – 60 = 40
సాధన x = 60, y = 40
∴ కార్లవేగం 60 కి.మీ./గం., 40 కి.మీ./గం.
![]()
రెండవ పద్దతి :
A కారు వేగం = 7 కి.మీ./ గం.
B కారు వేగం = y కి.మీ./గం. అనుకుందాం.
(i) రెండు కార్లు ఒకే దిశలో ప్రయాణించిన
సాపేక్ష వేగం V = x – y కి.మీ/గం.
దూరం (d) = 100 కి.మీ.
రెండు కార్లు ఒకే దిశలో ప్రయాణించిన 5 గం. తరువాత కలుస్తాయి.
∴ కాలం (t) = 5 గం.
కాలం × వేగం = దూరం
5 × (x – y) = 100
x – y = 5
x – y = \(\frac{100}{5}\) = 20
∴ x – y = 20. ……….. (1)
(ii) రెండు కార్లు ఎదురెదురు దిశలో ప్రయాణించిన సాపేక్షవేగం V = x + y కి.మీ./గం.
దూరం d = 100 కి.మీ.,
కాలము t = 1 గం|| (∵ 1 గంట తరువాత రెండు కార్లు కలుస్తాయి)
1 (x + y) = 100
x + y = 100 ………. (2)
(2) ⇒ y = 100 – x ని (1) లో రాయగా,
x – (100 – x) = 20
x – 100 + x = 20
2x = 20 + 100 = 120
x = \(\frac{120}{2}\) = 60
x = 60 ని (2) లో రాయగా,
60 + y = 100
⇒ y = 100 – 60 = 40
సాధన x = 60, y = 40
∴ A కారు వేగం X = 60 కి.మీ./గం.
B కారు వేగం y = 40 కి.మీ./గం.
![]()
ప్రశ్న 7.
రెండు కోణాలు పూరక కోణాలు. పెద్ద కోణము కొలత, చిన్న కోణము రెట్టింపు కన్నా 3° తక్కువ అయిన ఆ రెండు కోణాలను కనుగొనండి.
సాధన.
పెద్ద కోణం = x, చిన్న కోణం = y అనుకుందాం.
∴ రెండు కోణాలు పూరకాలు
∴ x + y = 90° ………. (1)
పెద్ద కోణం, చిన్న కోణం రెట్టింపు కన్నా 3° తక్కువ.
x = 2y – 3° …………. (2)
(2) ని (1) లో ప్రతిక్షేపించగా,
(2y – 3) + y = 90°
3y – 3 = 90°
3y = 90 + 3 = 93°
⇒ y = \(\frac{93}{3}\) = 31°
y = 31°ని (2) లో రాయగా,
x = 2 (31) – 3
⇒ x = 62 – 3 = 59°
సాధన x = 59°, y = 31°
పెద్ద కోణము = 59°, చిన్న కోణము = 31°
సరిచూచుట :
59° + 31° = 90° (పూరక కోణాలు)
2 × 31 – 3 = 61 – 3 = 59°.
![]()
ప్రశ్న 8.
ఒక బీజగణిత పాఠ్యపుస్తకంలో మొత్తము 1382 పేజీలు వున్నాయి. దీనిని రెండు భాగాలు చేసిన రెండవ భాగములో, మొదటి భాగము – కన్నా 64 పేజీలు ఎక్కువ వున్నాయి. అయిన ప్రతీ భాగములోని పేజీల సంఖ్యను కనుగొనండి.
సాధన.
మొదటి భాగంలోని పేజీల సంఖ్య = x అనుకుందాం.
రెండవ భాగంలోని పేజీల సంఖ్య = y అనుకుందాం.
పుస్తకంలోని మొత్తం పేజీలు 1382 కలవు.
∴ x + y = 1382 …………. (1)
రెండవ భాగంలో, మొదటి భాగము కన్నా 64 పేజీలు ఎక్కువ ఉన్నాయి.
y= x + 64 …….. (2)
(2) ను (1) లో ప్రతిక్షేపించగా,
x + (x + 64) = 1382
2x + 64 = 1382
2x = 1382 – 64
2x = 1318
⇒ x = \(\frac{1318}{2}\) = 659
x = 659 ను (2) లో రాయగా,
y = 659 + 64 = 723
సాధన x = 659, y = 723
మొదటి భాగంలోని పేజీల సంఖ్య = 659
రెండవ భాగంలోని పేజీల సంఖ్య = 723
సరిచూచుట :
659 + 723 = 1382
723 – 64 = 659.
![]()
ప్రశ్న 9.
ఒక రసాయనాలు అమ్మే దుకాణదారుని వద్ద రెండు రకాల హైడ్రోక్లోరిక్ ఆమ్ల ద్రావణాలున్నాయి. ఒకటి 50% ద్రావణము మరియు రెండవది 80% ద్రావణము. 100మి.లీ. 68% ద్రావణం కావాలన్న ఆ రెండు ద్రావణాలను ఎంత పరిమాణంలో తీసుకోవాలి ?
సాధన.
100 మి.లీ. 68% ద్రావణం కోసం తీసుకోవాల్సిన 50% హైడ్రోక్లోరికామ్లం = x మి.లీ..
80% హైడ్రోక్లోరికామ్లం = y మి.లీ. అనుకొందాం.
కావలసిన ద్రావణం పరిమాణం = 100 మి.లీ.
∴ x + y = 100 ……… (1) మరియు
x మి.లీ.లో 50% + y మి.లీ. 80%. = 100 మి.లీ.లో 68%
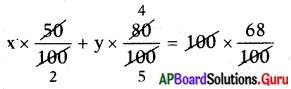
⇒ \(\frac{x}{2}+\frac{4 y}{5}\) = 68
⇒ \(\frac{5 x+8 y}{10}\) = 68
⇒ 5x + 8y = 680 …………….. (2)
(1) ⇒ y = 100 – x ను (2) లో రా యగా,
5x + 8 (100 – x) = 680
5x + 800 – 8x = 680
– 3x = 680 – 800
– 3x = – 120
3x = 120
x = \(\frac{120}{3}\) = 40
x = 40 ని (1) లో రా యగా,
40 + y = 100
y = 100 – 40 = 60
సాధన x = 40, y = 60. 100 మి.లీ.
68% ద్రావణం కోసం 50% హైడ్రోక్లోరికామ్ల ద్రావణం 40 మి.లీ. 68% హైడ్రోక్లోరికామ్ల ద్రావణం 60 మి.లీ. తీసుకోవాలి.
![]()
2వ పద్ధతి (చరరాశి తొలగింపు పద్ధతి) :
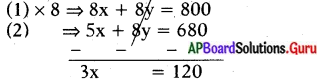
x = \(\frac{120}{3}\) = 40
x = 40ని (1) లో రాయగా,
40 + y = 100
⇒ y = 100 – 40 = 60
సాధన x = 40, y = 60.
100 మి.లీ. 68% ద్రావణం తయారుచేయుటకు 40 మి.లీ. 50% హైడ్రోక్లోరికామ్ల ద్రావణం, 60మి.లీ. 80% హైడ్రోక్లోరికామ్ల ద్రావణంలను కలపాలి.
సరిచూచుట :
40 మి.లీ. హైడ్రోక్లోరికామ్లం = 40 × \(\frac{50}{100}\)
= 20 మి.లీ.
60 మి.లీ. హైడ్రోక్లోరికామ్లం = 60 × \(\frac{80}{100}\) = 48
100 మి.లీ.లలో మొత్తం హైడ్రోక్లోరికామ్లం = 20 + 48 = 68 = 68%.
![]()
ప్రశ్న 10.
నీ వద్ద దాచుకొనుటకు ₹ 12000 సొమ్ము కలదనుకొనుము. దానిలో కొంత మొత్తాన్ని 10% వడ్డీరేటుకు మిగిలినది 15% వడ్డీరేటు వచ్చునట్లు పొదుపు చేయాలి. అయితే మొత్తము మీద పొదుపు 12% వడ్డీరేటు రావాలంటే ఏ వడ్డీరేటున ఎంత సొమ్ము దాచుకోవాలి ?
సాధన.
10% వడ్డీరేటున పొదుపు చేసినది = ₹ x
15% వడ్డీరేటున పొదుపు చేసినది = ₹ y అనుకొనుము.
పొదుపు చేసిన మొత్తము సొమ్ము = ₹ 12000 = x + y = 12000 …….. (1) మరియు
₹ x పై 10% వడ్డీ + ₹ y పై 15% వడ్డీ = 12000 పై 12% వడ్డీ
⇒ \(\frac{10}{100}\) x + \(\frac{15}{100}\) y = \(\frac{12}{100}\) × 12000
⇒ \(\frac{x}{10}+\frac{3 y}{20}\) = 1440
\(\frac{2 x+3 y}{20}\) = 1440
2x + 3y = 28800 ………. (2)
(1) ⇒ y = 12000 – x ను (2) లో ప్రతిక్షేపించగా,
2x + 3 (12000 – x) = 28800
2x + 36000 – 3x = 28800
⇒ – x = 28800 – 36000
⇒ – x = – 7200
⇒ x = 7200
x = 7200 ను (1) లో రా యగా 7200 + y = 12000
⇒ y = 12000 – 7200
⇒ y = 4800
సాధన x = 7200, y = 4800 – ₹ 12000 పై 12% వడ్డీరేటు రావాలంటే 10% వడ్డీరేటుకు ₹ 7200, 15% వడ్డీరేటుపై ₹ 4800 పొదుపు చేయాలి.
2వ పద్ధతి (చరరాశి తొలగించు పద్ధతి) :

x = 7200 ను (1) లో రాయగా
7200 + y = 12000
y = 12000 – 7200 = 4800
సాధన x = 7200, y = 4800.
₹ 12000 పై 12% వడ్డీరేటు వచ్చుటకు 10% వడ్డీరేటుపై ₹ 7200, 15% వడ్డీరేటుపై ₹ 4800 లు పొదుపు చేయాలి.
![]()
సరిచూచుట :
₹ 7200 పై 1 సం||కి 10% వడ్డీరేటున అవు వడ్డీ = \(\frac{7200 \times 1 \times 10}{100}\) = 720
₹ 4800 పై 1 సం||కి 15% వడ్డీరేటున అవు వడ్డీ = \(\frac{4800 \times 15}{100}\)= 720
మొత్తం వడ్డీ ₹ 720 + ₹ 720 = ₹ 1440
₹ 12000 పై 12% వడ్డీ = 12000 × \(\frac{12}{100}\) = 1440
