AP 10th Class Maths Important Questions Chapter 10 Mensuration

These AP 10th Class Maths Chapter Wise Important Questions Chapter 10 Mensuration will help students prepare well for the exams.

AP State Syllabus 10th Class Maths 10th Lesson Important Questions and Answers Mensuration

Question 1.
Find the volume of a sphere of radius 21cm.(Take π = 22/7)
Solution:
Volume of the sphere = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) × \(\frac{22}{7}\) × 21 × 21 × 21 = 38,808(cm)³

Question 2.
Find the total surface area of a hemisphere, whose radius is 7 cm.
Solution:
Radius of Hemisphere, r = 7 cm
T.S.A of Hemisphere = 3πr²
= 3 × \(\frac{22}{7}\) × 7 × 7 = 462 (cm)²

Question 3.
Find the volume of right circular cone with radius 3 cm. and height 14 cm.
Solution:
Volume of right circular cone = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 3 × 3 × 14 = 132 cm³

Question 4.
Find the curved surface area of cylinder, whose radius is 7 cm. and height is 10 cm.
Solution:
Radius of a cylinder = r = 7 cm
Height of a cylinder = h – 10 cm
CSA of a cylinder = A = 2πrh
= 2 × \(\frac{22}{7}\) × 7 × 10
= 44 × 10 = 440 sq.cm

Question 5.
The surface area of a football is 616 cm², then find the radius of that ball. ( π = 22/7).
Solution:
Surface area of a football (sphere) = 4πr².
4πr² = 616
πr² = 154
r² = 154 × \(\frac{7}{22}\)
r² = 7 × 7 = 49
∴ r = 7 cm

Question 6.
The volume of a cylinder is 448π cm³ and height is 7 cm. What is its radius?
Solution:
Volume of the cylinder = πr²h = 448π
Here h = 7cm ,r = r
then πr² × 7 = 448π
r² = \(\frac{448}{7}\) = 64
∴ Radious (r) = 8 cm

Question 7.
Find the surface area of a sphere of radius 14 cm. (Take π = \(\frac{22}{7}\))
Solution:
Radius of given sphere = (r) = 14 cm
Formula for surface area of sphere = 4πr²
∴ Surface area of given sphere = 4 × \(\frac{22}{7}\) × 14 × 14 = 88 × 28 = 2464 cm²

Question 8.
Draw a rough diagram of a solid, showing the combination of a cone and cylinder, whose base radii are same.
Answer:

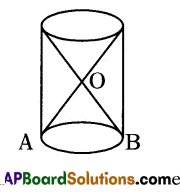
AB is radius of cylinder as well as cone.

Question 9.
Find the area of the paper sheet required to make a conical joker cap with radius 7 cm and slant height 14 cm.
Solution:
Given, radius = 7 cm
Slant height = 14 cm
Area of paper sheet = πrl
= \(\frac{22}{7}\) × 7 × 14
= 22 × 14 = 308 cm²

Question 10.
If the diameter of a sphere is equal to the side of a cube, find the ratio of their volumes.
Solution:
Let diameter of the sphere = d = side of the cube
∴ Radius of the sphere (r) = \(\frac{\mathrm{d}}{2}\)
volume of the sphere = \(\frac{4}{3}\)πr³
= \(\frac{4}{3}\)π(\(\frac{\mathrm{d}}{2}\))³ = \(\frac{4}{3}π\)\(\frac{\mathrm{d}^{3}}{8}\) = \(\frac{\pi}{6}\) d³
And, volume of the cube = d³
∴ The ratio of volume of sphere to volume of cube = \(\frac{\pi}{6}\) d³ : d³ = \(\frac{\pi}{6}\) : 1

Question 11.
Find the volume and total surface area of a hemisphere whose radius is 35 cm?
Solution:
Radius of the hemisphere (r) = 35 cm.
Volume of the hemisphere = \(\frac{2}{3}\) πr³
= \(\frac{2}{3} \times \frac{22}{7}\) × 35 × 35 × 35

Total surface area = 3πr²
= 3 × \(\frac{22}{7}\) × 35 × 35 = 11550 cm²

Question 12.
A solid iron rod has a cylindrical shape. Its height is 11 cm and base diameter is 7 cm. Then find the total volume of 50 rods.
Solution:
The height of the cylinderical
Rod (h) = 11 cm,
Raidus (r) = 7/2 cm
Volume = πr²h = \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) × 11
= 423.5 (cm)³
Volume of 50 rods = 50 × 423.5 = 21175 (cm)³

Question 13.
Two cubes each of volume 125 cm³ are joined end to end together. Find the total surface area of the resulting cuboid.
Solution:
Volume of each cube = 125 cm³
∴ a³ = 125 cm³ ⇒ a = 5 cm

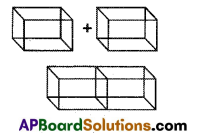
By joining these two cubes we get a cuboid, whose
length (l) = 10 cm
breadth (b) = 5 cm
height (h) = 5 cm
then the total surface area
= 2 (lb + bh + lh)
= 2(10(5) + 5(5) + 5(10))
= 2(50 + 25 + 50)
= 2(125) = 250 cm²

Question 14.
The base area of a cone is 616 sq.cm and its height is 48 cm. Find its total surface area.
Solution:
The base area of a cone = πr² = 616 cm²
Given height of cone = 48 cm = h

∴ Total surface area
= C.S.A + base area
= 2200 + 616 = 2816 cm²

Question 15.
Find the volume of largest right circular cone that can be cut out from a cube, whose edge is 7 cm.
Solution:
Volume of the cone (V) = \(\frac{1}{3}\) πr²h
[r = \(\frac{s}{2}=\frac{h}{2}\)]
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) × 7
∴ V = 89.83 cm³

Question 16.
If half of the vertical angle of a cone of height 3 cm is 60°. Find its volume.
Solution:

Let ‘B’ be the centre of base of the cone and BC is radius.
AB is vertical height (i.e.,)
AB = 3 cm
Given that ∠BAC = 60°
ΔABC is a right angled triangle, then
tan 60° = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
⇒ √3 = \(\frac{\mathrm{BC}}{3}\) ⇒ BC = 3√3 cm
Now we have h = 3 cm, r = 3√3 cm
Volume of the cone = \(\frac{1}{3}\) πr²h
\(\frac{1}{3}\) π(3√3)² × 3 = 27π cm³
(or)
= \(\frac{594}{7}\) = 84.86 cm³

Question 17.
Find the volume and total surface area of a hemisphere of diameter 7 cm. Take π = \(\frac{22}{7}\)
Solution:
Diameter of hemisphere = 7 cm
∴ Radius of hemisphere = (r) = \(\frac{d}{2}=\frac{7}{2}\) cm
Then volume of hemisphere = V = \(\frac{2}{3}\)πr³
= \(\frac{2}{3} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times \frac{7}{2}\) = \(\frac{22 \times 49}{12}\) = 89.83
Volume = 89.83 cm³
Total surface area of hemisphere = 3πr²
= 3 × \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) = \(\frac{77 \times 3}{2}\) = 115.5 cm²

Question 18.
The length, breadth and height of a cuboid are (log 125 + log 8),
(log 1000 – log 10) and log 10 respectively. Find the total surface area of the cuboid.
Solution:
Length of cuboid (l) = (log 125 + log 8)
Breadth of cuboid (b)
= (log 1000 – log 10)
Height of cuboid (h) = log 10
∴ (l) = log (125 × 8)
= log 1000
= log 10³ = 3 log 10 = 3

(b) = log 1000 – log 10
= log \(\frac{1000}{10}\)
= log 100 = log 10² = 2
(h) = log 10 = 1
Then total surface area of cuboid
= 2(lb + bh + lh)
= 2(3 × 2 + 2 × 1 + 1 × 3)
= 2 (6 + 2 + 3) = 2(11)
= 22 square units.

Question 19.
The radius of a sphere is 3.5 cm. Find it’s surface area.
Solution:
Given, r = 3.5 cm
Surface area of sphere = 4πr²
= 4 × \(\frac{22}{7}\) × 3.5 × 3.5
= \(\frac{88 \times 12.25}{7}\) = 154 cm²

Question 20.
Express the volume of a cone in terms of volume of right circular cylinder of the same base and height and explain how you arrived at it.
Solution:
We know that,
Volume of cone = \(\frac{1}{3}\) πr²h
Volume of cylinder = πr²h
Hence,
volume of cone : volume of cylinder
= \(\frac{1}{3}\) πr²h : πr²h
Hence, volume of cone = \(\frac{1}{3}\) × volume of cylinder.

Question 21.
The radius of a conical tent is 5m and its height is 12m. Calculate the length of the canvas used in making the tent if width of canvas is 2cm.
Solution:
Radius of the conical sent (r) = 5 m.
Height of the tent (h) = 12 m.
∴ Slant height of the cone
(l) = \(\sqrt{r^{2}+h^{2}}\)
= \(\sqrt{5^{2}+12^{2}}\)
= \(\sqrt{25+144}\) = \(\sqrt{169}\) 13 m.
Now, surface area of the tent = πrl
= \(\frac{22}{7}\) × 5 × 13 = \(\frac{1430}{7}\) m²
Area of the canvas used = \(\frac{1430}{7}\) m²
It is given that the width of the canvas = 2m.
Length of the canvas used = \(\frac{\text { Area }}{\text { Width }}\)
= \(\frac{1430}{7} \times \frac{1}{2}\)
= 102.14 m

Question 22.
How many spherical balls can be made out of a solid cube of lead, whose edge measures 66 cm. and each ball being 3 cm in radius ?
Solution:
Side of the cube (s) = 66 cm
Radius of the spherical ball = r = 3 cm
Let the number of spherical balls that can be made = n
n × volume of a spherical ball = Volume of the cube
n × \(\frac{4}{3}\)πr³ = s³
n × \(\frac{4}{3} \times \frac{22}{7}\) × 3 × 3 × 3 = (66)³
n = 66 × 66 × 66 × \(\frac{3}{4} \times \frac{7}{22} \times \frac{1}{3} \times \frac{1}{3} \times \frac{1}{3}\)
= 2541
Number of spherical balls can be made = 2541

Question 23.
An oil drum is in the shape of cylinder, whose diameter is 2 m and height is 7 m. The painter charges ? ₹ 5 per m² to paint the drum. Find the total charges to be paid to the painter for
10 drums.
Solution:
It is given that diameter of the (oil drum) cylinder = 2 m.
Radius of cylinder = \(\frac{\mathrm{d}}{2}=\frac{2}{2}\) = 1 m.
Total surface area of a cylindrical drum = 2πr(r + h)
= 2 × \(\frac{22}{7}\) × 1(1 + 7)
= 2 × \(\frac{22}{7}\) × 8 = \(\frac{352}{7}\)m² = 50.28 m².
So, the total surface area of a drum = 50.28 m²
Painting charge per 1 m² = ₹ 5.
Cost of painting of 10 drums
= 50.28 × 5 × 10
= ₹ 2514

Question 24.
A hemisphere is cut out from one face of a cubical wooden block of edge 21 cm, such that the diameter of the hemisphere is equal to the edge of the Cube. Determine the total surface area of the remaining block.
Solution:
Let diameter of the hemisphere be ‘l’ = 21 cm
Radius of the hemisphere = \(\frac{l}{2}=\frac{21}{2}\) cm
Also, length of the edge of the cube = l = 21 cm
∴ Total surface area of the remaining solid .

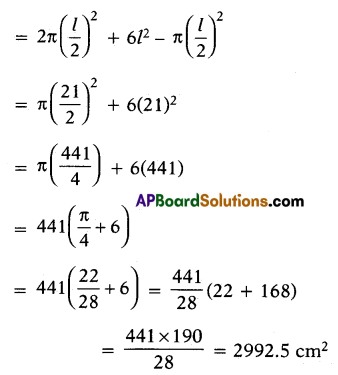
Question 25.
Two metallic spheres of radii 6 cm and 8 cm are melted along with another sphere and made into a big sphere of radius 12 cm. Find the radius of the third sphere.
Solution:
Radii of two metallic spheres
= r₁ = 6 cm
r = 8 cm
Volume of the metallic spheres

⇒ 728 + x³ – 12³
⇒ x³ = 12³ – 728 = 1728 – 728
= 1000 cm
⇒ x = 10 cm.

Question 26.
Two cubes each of volume 216 cm³ are joined end to end together. Find the total surface area of the resulting cuboid.
Solution:
Given, volume of the cube V = a³ = 216 cm³
∴ a³ = 6 × 6 × 6 = 6³
Hence a = 6 cm

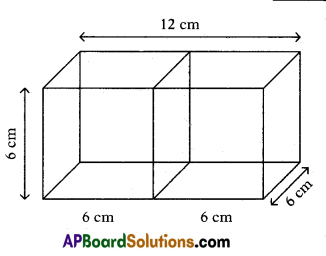
When two cubes are added, the length of cuboid = 2a = 2 × 6 = 12 cm,
breadth = a = 6 cm,
height = a = 6 cm is formed.
∴ T.S.A. of the cuboid = 2(lb + bh +lh)
= 2(12×6 + 6×6 + 12×6)
= 2(72 + 36 + 72)
= 2 × 180 = 360 cm²
∴ The surface area of resulting cuboid is 360 cm².

Question 27.
What is area of required cloth to make 10 conical hats having 7 cm ground radius and 24 cm height ?
Solution:

Ground radius of cone (r) = 7 cm
Height of cone (h) = 24 cm
Then its slant height
l = \(\sqrt{r^{2}+h^{2}}\)
= 7² + 24²
= \(\sqrt{49+576}\)
l = \(\sqrt{625}\) = 25 cm
Then C.S.A. of the cone = Area of cloth required
= πrl = \(\frac{22}{7}\) × 7 × 25 = 550 cm²
Then the cloth required for 10 hats = 550 × 10 = 5500 cm²

Question 28.
A circle having 21 cm radius is cut into 3 equal parts to make 3 equal circular cones. Then what will be the radius of such cone ?
Solution:
Radius of the circle = 21 cm
Then the circumference of circle
= 2πr = 2 × \(\frac{22}{7}\) × 21 = 132 cm
\(\frac{1}{3}\) of this circumference of circle = Circumference of the ground of the
cone
= \(\frac{1}{3}\) × 132 = 44 cm
Now let the ground radius of new cone = r
Then its ground circumference = 2πr = 44

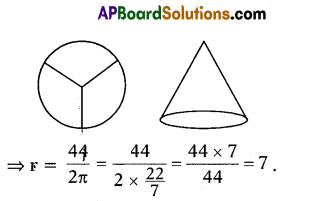
So ground radius of cone = 7 cm.

Question 29.
Define “Regular cone”. Deduce formula for slant height of a regular cone.
Solution:

A solid having a circular base and vertex above the centre of circular base is called a regular cone.
A → Vertex
‘O’ centre of ground
OB is the radius of cone (r) and
0A is the height of cone (h)
AB is slant height (l)
Now ΔAOB is a right angled triangle.
Where ∠AOB = 90 and AB is hypotenuse.
Then from Pythagorus theorem
AB² = OA² + OB² = r² + h²
∴ AB = \(\sqrt{r^{2}+h^{2}}\)
∴ Slant hight (l) = \(\sqrt{r^{2}+h^{2}}\)

Question 30.
Draw a cone and label them.
Solution:

In the above cone
OB is the radius of the ground.
AO is the height of cone.
AB is slant height of cone.

Question 31.
Which kind of cones are formed by rotating on their axis of following triangles?
a) Equilateral
b) Right angled
c) Scalene
Solution:
a) Equilateral triangle : Having the altitude of this equilateral as rotat¬ing axis, on rotation we get a regular cone, (right cone)

b) Right angled triangle : Having a leg (a side other than hypotenuse) as rotating axis, on rotation of this right angled triangle we get a right circular cone.

c) Scalene triangle : Having a particular altitude from a vertex as rotating axis, on rotation we get a
cone

Question 32.
A sphere, a cylinder and a cone have the same radius and same height. Find the ratio of their volumes. (AS₄) [Hint: Diameter of the sphere is equal to the heights of the cylinder and the cone.] A sphere, a cylinder and a cone have the same radius and same height.
Solution:
Sphere Cylinder Cone
Radius = r r r
Height = r 2r = h 2r = h

Now C.S.A of spehre = 4πr² …………….(1)
C.S.A of cylinder = 2πrh
= 2πr.2r-2r = 4πr² ……………….. (2)
Now for cone, slant height = l
= \(\sqrt{r^{2}+h^{2}}\)
= \(\sqrt{r^{2}+4 r^{2}}\) ( ∵ h = 2r)
= \(\sqrt{5 r^{2}}\) = √5(r)
Then C.S.A of cone = πrl = πr. √5r
= √5 πr² ……………. (3)
∴ Ratio of C.S.A of sphere, cylinder and cone = 4πr² : 4πr² : √5 πr²
= 4 : 4 : √5