AP 10th Class Maths Bits Chapter 10 Mensuration with Answers

Practice the AP 10th Class Maths Bits with Answers Chapter 10 Mensuration on a regular basis so that you can attempt exams with utmost confidence.

AP State Syllabus 10th Class Maths Bits 10th Lesson Mensuration with Answers

Question 1.
The total surface area of a cube is 54 cm², then find its side.
Answer:
3 cm
Explanation:
TSA = 6s² = 54
⇒ side² = 9 ⇒ side = 3 cm.

Question 2.
Base area of a regular cylinder is 154 cm², then find its radius.
Answer:
7 cm
Explanation:
πr² = 154
⇒ r² = 154 × \(\frac{7}{22}=\frac{14 \times 7}{2}\) × 7 × 7
⇒ r = 7 cm

Question 3.
If the height and radius of a cone are 15 cm and 8 cm, then find its slant height
Answer:
17 cm
Explanation:

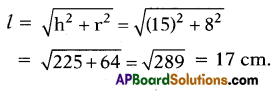
Question 4.
Write a formula to find curved surface area of a hemisphere.
Answer:
2πr²

Question 5.
How much the volume of a cube having 1 cm side ?
Answer:
1 cm³

Question 6.
Ratio of volumes of two spheres is 8 : 27, then find ratio of their curved surface area.
Answer:
4 : 9
Explanation:

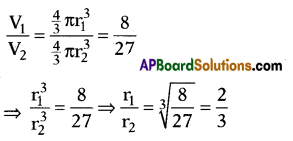
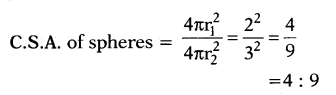
Question 7.
Football is in a model of …………..
Answer:
sphere

Question 8.
If the volume of a cube is 216 cm³, then find its side.
Answer:
6 cm
Explanation:
S³ = 216 ⇒ Side = \(\sqrt[3]{216}\) = 6 cm

Question 9.
Find the curved surface area of a right circular cylinder.
Answer:
2πrh

Question 10.
Find the curved surface area of a sphere will be……………. whose radius
is 10 cm.
Answer:
400 π

Question 11.
Find the volume of a cube will be ………….. (in cm³), whose total surface area is 216 cm².
Answer:
216
Explanation:
6S² = 216
⇒ S² = \(\frac{216}{6}\) = 36
⇒ S = \(\sqrt{36}\) = 6
∴ Volume = S³ = 6³ = 216

Question 12.
Write the name of a famous book writ-ten by ancient mathematician Aryabhatta.
Answer:
Aryabhatteeyam.

Question 13.
Which of the following vessel can be filled with more water (A, B are in cylindrical shape)?

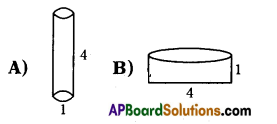
Answer:
B)

Question 14.
Find the volume of right circular cylinder with radius 6 cm and height 7 cm.
Answer:
792 cm³

Question 15.
A sphere of radius ‘r’ inscribed in a cylinder. The surface area of the sphere …………… of the cylinder.
Answer:
Curved surface area.

Question 16.
How much the maximum length of the stick that can be placed in a cuboid, whose measurements are 8 × 4 × 1?
Answer:
9

Question 17.
A cylinder and cone have bases of equal radii and are of equal heights, then find their volumes are in the ratio.
Answer:
3 : 1

Question 18.
Find the total surface area of a solid hemisphere of radius 7 m.
Answer:
147 π sq.m.
Explanation:
3πr² = 7² × 3 × π = 147π sq.m.

Question 19.
Radius of a cone is ‘r’, height is ‘h’ and its slant height is ‘l’, then which of the following is false ?
Answer:
Always r > p

Question 20.
Radius, height, slant height of a cone are r, h, ‘l’, then 7′ value in terms of r and h.
Answer:
\(\sqrt{r^{2}+h^{2}}\)

Question 21.
Volumes of two spheres are in the ratio of 8:27. Find the ratio of their surface areas.
Answer:
4 : 9

Question 22.
A solid ball is exactly fitted inside the cubical box of side ‘a’. Find the volume of the ball.
Answer:
\(\frac{1}{6}\) πa³

Question 23.
If the total surface area of cube is 96 cm³, then find side of cube.
Answer:
4 cm

Question 24.
Base area of the prism is 30 cm² and its height is 10 cm. Then find the volume of the prism.
Answer:
300 cm³

Question 25.
The volume of a cone with base radius 7 cm is 462 c.c., find its height.
Answer:
9 cm

Question 26.
If total surface area of a cube is 96 cm², then find its volume.
Answer:
64 cm³

Question 27.
Find the volume of cone, whose radius is 3 cm and height is 8 cm.
Answer:
24 π

Question 28.
Write a formula to find total surface
area of cone in sq. units. f
Answer:
πr² + πrl

Question 29.
Find the volume of a hemisphere of radius 3.5 cm is …………… cm³.
Answer:
89.83

Question 30.
In the above problem find TSA = ………………… cm².
Answer:
115.5

Question 31.
Write a combination of a shuttle cock.
Answer:
Hemisphere, frustum cone

Question 32.
The volume of cone is 462 cm³, r = 7 cm, then find h is ……………… cm.
Answer:
9

Question 33.
10³ (cm)³ = ……………. litre.
Answer:
1

Question 34.
In l² = h² + r², h = 15, r = 8, then l = ………………
Answer:
17

Question 35.
The perimeter of an equilateral triangle is 60 cm, then find its area (in cm²).
Answer:
173.2

Question 36.
Write the number of faces of a cuboid.
Answer:
8

Question 37.
If the ratio of radii of two spheres is 2:3, then find the ratio of their surface areas.
Answer:
4 : 9

Question 38.
Write a formula to find volume of sphere in …………….. cu. units.
Answer:
\(\frac{4}{3}\)πr³

Question 39.
In a hollow cuboid box of size 4 × 3 × 2 m, find the number of solid iron spherical balls of radius 0.5 m that can be packed.
Answer:
24

Question 40.
In a cone, r = 7 cm, h = 10 cm, then find l = cm.
Answer:
12.2

Question 41.
Find T.S.A of a solid hemisphere whose radius is 7 cm.
Answer:
147π

Question 42.
Find the total surface area of hemisphere of radius ’r’.
Answer:
3πr²

Question 43.
If the length of each diagonal of a cube is doubled, then how many times its volume becomes.
Answer:
8

Question 44.
Who gave the symbol π?
Answer:
Euler

Question 45.
Find the surface area of a cube, whose side is 27 cm.
Answer:
4374 cm³

Question 46.
Find the volume of cone if r = 2 cm, h= 4 cm.
Answer:
\(\frac{16}{3}\)π cm³
Explanation:
Volume of cone = \(\frac{1}{3}\) πr²h
\(\frac{1}{3}\) × π × 4 × 4 = \(\frac{16}{3}\)π cm³

Question 47.
Write the number of edges of a cuboid has.
Answer:
12

Question 48.
Find the volume of a right circular cone with radius 6 cm and height 7 cm is …………….. cm³.
Answer:
264
Explanation:
Volume of right circular cone V = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) . π . 6² . 7 = 264 cm³.

Question 49.
If a right angled triangle is revolved about its hypotenuse, then find it will form a ……………..
Answer:
Double cone

Question 50.
Write a formula to find CSA of cylinder ……………… sq. units.
Answer:
2πrh

Question 51.
Volume of cuboid = ………….. cu.units.
Answer:
lbh

Question 52.
Write a formula to find surface area of sphere ……………. in sq. units.
Answer:
4πr²

Question 53.
Total surface area of a cube is 216 cm², then find its volume.
Answer:
216

Question 54.
If the radii of circular ends of a frustum of a cone are 20 cm and 12 cm and its height is 6 cm, then find the slant height of the frustum.
Answer:
10

Question 55.
If the external and internal radii of a hollow hemispherical bowl are R and r, then find its total surface area.
Answer:
π (3R² + r²)

Question 56.
Rational value of π = …………………
Answer:
22/7

Question 57.
A cylinder, a cone and a hemisphere are of equal base and have the same height, then find the ratio of their volumes.
Answer:
3 : 1 : 2
Explanation:
Cylinder, Cone, Hemisphere have equal base and same height. So, the height will become radius.
= Volume of cylinder: Volume of cone : Volume of hemisphere
= πr²h : \(\frac{1}{3}\) πr²h : \(\frac{2}{3}\) πr²h
= \(\frac{1}{3}\) πr³ : \(\frac{2}{3}\) πr³ : πr³
= 1 : \(\frac{1}{3}\) : \(\frac{2}{3}\) = 3 : 1 : 2

Question 58.
A solid sphere of radius 10 cm is moulded into 8 spherical solid balls of equal radius, then find radius of small spherical balls.
Answer:
5
Explanation:
Volume of sphere = 8 (volume of one spherical ball)

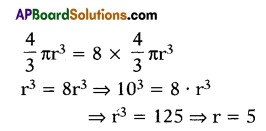
Question 59.
Write a formula to find CSA of cone = ………………… sq. units.
Answer:
πrl

Question 60.
Find the total surface area of a solid hemisphere of radius 7 cm.
Answer:
239π cm²

Question 61.
The volume of a vessel in the form of a right circular cylinder is 448π cm³ and its height is 7 cm, then find the radius of the base.
Answer:
8 cm

Question 62.
If the diameter of a sphere is’d’, then find its volume.
Answer:
\(\frac{1}{6}\) πd²

Question 63.
Write a formula to find total surface area of cylinder in ……………….. sq. units.
Answer:
2πrh+ 2πr²

Question 64.
In a cylinder, r= 7 m, h=15 m, then find V.
Answer:
2310 m³.

Question 65.
If the diagonals of a rhombus are 10 cm and 24 cm, then find area in ………………… cm².
Answer:
120

Question 66.
Find the curved surface area of a right circular cone of height 15 cm and base diameter is 16 cm.
Answer:
136π cm²

Question 67.
Find the number of balls, each of radius 1 cm that can be made from a solid sphere of radius 8 cm.
Answer:
512

Question 68.
Volume of hemisphere is19404 cm³, then find its TSA (in cm²).
Answer:
4158

Question 69.
r³ = 1728, then find ‘r’.
Answer:
12

Question 70.
In a cone, d = 14 cm, l = 10 cm, then find CSA = ……………….. cm².
Answer:
220

Question 71.
In the figure, P = …………………

Answer:
h² + r²

Question 72.
The surface area of a sphere is 616 sq.cm, then find its radius in …………. cm.
Answer:
7

Question 73.
In a hemisphere, r = 7 cm, then find CSA (in cm²)
Answer:
308

Question 74.
Write a formula to find volume of hollow cylinder.
Answer:
(πR² – r²)

Question 75.
In a cube, a = 4 cm, then find TSA (in cm²).
Answer:
90

Question 76.
In a cylinder, h=14 cm, V= 176 cm³, r = …………….. cm.
Answer:
2

Question 77.
In a hemisphere, r = 1.75 cm, then find CSA (in cm²).
Answer:
38.5

Question 78.
TSA of a cylinder is 1188 cm², h = 20 cm (in cm), then find its volume.
Answer:
3080

Question 79.
Heap of stones is an example of ………………
Answer:
Cone

Question 80.
Write a formula to find diagonal of rectangle.
Answer:
\(\sqrt{l^{2}+b^{2}}\)

Question 81.
The area of the base of a right circular cone is 78.5 cm². If its height is 12 cm, then find its volume (in cm³).
Answer:
314

Question 82.
Surface area of a sphere and cube are equal, then find the ratio of their volumes.
Answer:
√π : √6
Explanation:

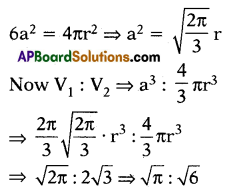
Question 83.
A conical flask is full of water. The flask has base radius r and height h. The water is poured into a cylindrical flask of base radius mr. Find the height of water in the cylindrical flask.
Answer:
\(\frac{\mathrm{h}}{3}\) m²

Question 84.
Find the volume of the greatest cylinder that can be cut from a solid wooden cube of length of edge 14 cm.
Answer:
2156 cm³

Question 85.
The area of equilateral triangle is 36√3 cm², then find the perimeter (in etn).
Answer:
36
Explanation:
Area 36√3 cm² ⇒ \(\frac{\sqrt{3} a^{2}}{4}\) = 36√3
⇒ a² = 36 × 4
⇒ a = 6 × 2 = 12 cm
Perimeter = 3a = 3 × 12 = 36 cm.

Question 86.
Base circumference of a cylinder is 220 cm and height is 63 cm, then find CSA (in cm²).
Answer:
13860

Question 87.
Write a formula to find area of equi¬lateral triangle of side ‘a’ units (in sq. units).
Answer:
\(\frac{\sqrt{3}}{4}\)a²

Question 88.
A solid iron cuboid of dimensions 49 × 33 × 24 cm is melted to form a solid sphere, then find its radius.
Answer:
21 cm

Question 89.
A cone and a hemisphere have equal bases and equal volumes, then find the ratio of their heights.
Answer:
2 : 1

Question 90.
Laddu is an example of ……………
Answer:
Sphere

Question 91.
Write a formula to find total surface area of a cube (in sq. units).
Answer:
6l²

Question 92.
The height of a cylinder is doubled and radius is tripled, then how many times its curved surface area will become.
Answer:
6 times
Explanation:
CSA of cylinder is 2πrh, if radius is tripled and height is doubled, then CSA = 2π . 3r . 2h = 12πrh = 6(2πrh)

Question 93.
Write a formula to find volume of hemisphere (in cu. units).
Answer:
\(\frac{2}{3}\)πr³

Question 94.
The surface areas of two spheres are in the ratio 1 : 4, then find ratio of their volumes.
Answer:
1 : 64

Question 95.
Write the diameter of a sphere which can inscribe a cube of edge ‘x’ cm.
Answer:
x

Question 96.
The volume of a cube is 216 cm³, then find its edge.
Answer:
6

Question 97.
Write a formula find volume of cylinder (in cu. units).
Answer:
πr²h

Question 98.
Find the ratio of volume of a cone and cylinder of equal diameter and height.
Answer:
1 : 3

Question 99.
Write a formula to find volume of a cube (in cu. units).
Answer:
a³

Question 100.
The sphere of radius 2.1 cm, then find its volume (in cm³).
Answer:
38.08

Question 101.
A sphere, a cylinder and a cone have the same radius, then find the ratio of their curved surface areas.
Answer:
4 : 4 : √5

Question 102.
If the diagonal of a cube is 2.5 m, then find its volume (in m³).
Answer:
\(\frac{5.2}{\sqrt{3}}\)
Explanation:
Applying Pythagoras theorem,
(2.5)² = [a² + (√2a)²]
⇒ 6.25 = 3a²
⇒ a² = \(\frac{6.25}{3}\) ⇒ a = \(\frac{2.5}{\sqrt{3}}\) m³
Volume of cube = a³
\(\left(\frac{2.5}{\sqrt{3}}\right)^{3}\) = \(=\frac{15.625}{3 \sqrt{3}}=\frac{5.2}{\sqrt{3}}\) m³

Question 103.
A heap of rice is in the form of a cone of diameter 12 m and height 8 m, then find the volume (in m³).
Answer:
301.71

Question 104.
Perimeter of square is 20 cm, find then area (in cm²).
Answer:
25

Question 105.
CSA of a cone is 4070 cm² and its diameter is 70 cm, then find slant height.
Answer:
37

Question 106.
The volume of a cuboid is 3,36,000 cm³. If its area is 5,600 cm², then find h. (in cm).
Answer:
60

Question 107.
Write a formula to find diagonal of a cuboid.
Answer:
\(\sqrt{l^{2}+b^{2}+h^{2}}\)

Question 108.
Find the volume of the largest right circular cone that can be cut out from a cube of edge 4.2 cm.
Answer:
19.4 cm³

Question 109.
The diameter of a metallic sphere is 6 cm and melted to draw a wire of diameter 2 cm, then find the length of the wire.
Answer:
9 cm
Explanation:
Volume of sphere = Volume of cylinder
\(\frac{4}{3}\)πr³ = πr²h
⇒ \(\frac{4}{3}\) × 3³ = h × 2²
⇒ 4 × 9 = h × 4 ⇒ h = 9 cm

Question 110.
The volume and surface area of a sphere are numerically equal. Then find the volume of the smallest cylinder in which the sphere is exactly kept.
Answer:
54π

Question 111.
Write a formula to find volume of cone with’d’ as diameter and ’h’ as height is ………………. cu. units.
Answer:
\(\frac{\pi \mathrm{d}^{2} \mathrm{~h}}{12}\)

Question 112.
An iron cylindrical rod has a height 4 times its radius is melted and cast into spherical balls of the same radius. Find the number of balls cast.
Answer:
6
Explanation:
Volume of cylinder = n × Volume of sphere
πr²h = n × \(\frac{4}{3}\)πr³
πr²(8r) = n × \(\frac{4}{3}\)πr³
n = \(\frac{24}{4}\) = 6
∴ Number of balls = 6.

Question 113.
If a cone is cut into two parts by a horizontal plane passing through the mid point of the axis, find the ratio of the volumes of the upper part and the cone.
Answer:
1 : 8

Question 114.
In a cylinder, r = 8 cm, h = 10 cm, then CSA = ……………….. cm³
Answer:
\(\frac{3520}{7}\)

Question 115.
In a cone, (l + r)(l – r) = …………..
Answer:
h²

Question 116.
A solid sphere of radius r melted and recast into the shape of a solid cone of height r, then find radius of the base of the cone.
Answer:
2r

Question 117.
If the radius of base of a cylinder is doubled and the height remains un-changed, its C.S.A becomes.
Answer:
3 times

Question 118.
Write a formula to find volume of cone, (in cu. units).
Answer:
\(\frac{1}{3}\)πr²h

Question 119.
Write a formula to find diagonal of a cube (in units).
Answer:
a√3

Question 120.
The ratio of volume of two cones is 4 : 5 and the ratio of the radii of their base is 2 : 3, then find ratio of their vertical heights.
Answer:
9 : 5

Question 121.
Find the number of cubes of side 2 cm which can be cut from a cube of side 6 cm.
Answer:
27

Question 122.
A cuboid has dimensions 10 × 8 × 6 cm, then find its volume (in cm³).
Answer:
480

❖ Choose the correct answer satisfying the following statements.
Question 123.
Statement (A): The slant height of the frustum of a cone is 5 cm and the difference between the radii of its two circular ends is 4 cm. Than the height of the frustum is 3 cm.
Statement (B) : Slant height of the frustum of the cone is given by
l = \(\sqrt{(\mathrm{R}-\mathrm{r})^{2}+\mathrm{h}^{2}}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
i) Both A and B are true.
Explanation:
We have, L = 5 cm, R – r = 4 cm
∴ 5 = \(\sqrt{(4)^{2}+\mathrm{h}^{2}}\)
⇒ 16 + h² = 25
⇒ h² = 25 – 16 = 9
⇒ h = 3 cm
Hence, (i) is the correct option.

Question 124.
Statement (A) : If the volumes of two spheres are in the ratio 27 : 8. Then their surface areas’are in the ratio 3 : 2.
Statement (B) : Volume of the sphere
= \(\frac{4}{3}\) πr³ and its surface area = 4πr³.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
iv) Both A and B are false.
Explanation:

Hence, (iv) is the correct option.

Question 125.
Statement (A) : Two identical solid cube of side 5 cm are joined end to end. Then total surface area of the resulting cuboid is 300 cm².
Statement (B): Total surface area of a cuboid is 2(lb + bh + lh).
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
iii) A is false, B is true.
Explanation:
When cubes are joined end to end, it will form a cuboid.
∴ l = 2 × 5 = 10 cm, b = 5 cm and h = 5 cm
∴ Total surface area = 2 (lb + bh + lh) = 2(10 × 5 + 5 × 5 + 10 × 5)
= 2 × 125 = 250 cm²
Hence, (iii) is the correct option.

Question 126.
Statement (A) : The number of 90ms 1.75 cm in diameter and 2 mm thick if formed from a melted cuboid 10 cm × 5.5 cm × 3.5 cm is 400.
Statement (B) : Volume of a cylinder = πr²h cubic units and area of cuboid = (l × b × h) cu. units.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
i) Both A and B are true.
Explanation:

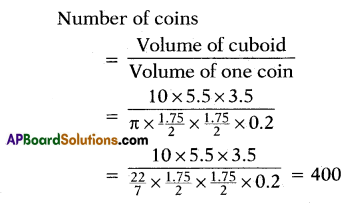
Hence, (i) is the correct option.

Question 127.
Statement (A) : The radii of two cones are in the ratio 2 : 3 and their volumes in the ratio 1 : 3. Then the ratio of their height is 3 : 2.
Statement (B) :
Volume of the cone = \(\frac{1}{3}\)πr²h
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
iii) A is false, B is true.
Explanation:
We have, ratio of volume

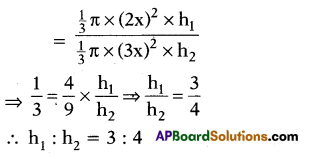
Hence, (iii) is the correct option.

Question 128.
Statement (A) : The curved surface area of a cone of base radius 3 cm and height 4 cm is 15 π cm².
Statement (B): Volume of a cone = \(\frac{1}{3}\)πr²h
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
i) Both A and B are true.

Question 129.
Statement (A): If the surface area of a sphere is 616 cm². Then its radius 6 cm.
Statement (B): Surface area of sphere = 4πr²sq. units.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
iii) A is false, B is true.

Question 130.
Statement (A) : A hemisphere of radius 7 cm is to be painted outside on the surface of it. The total cost of painting at ₹ 5 per cm2 is ₹ 2300.
Statement (B): The total surface area of a hemisphere is 3πr²sq. units.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
iii) A is false, B is true.

Question 131.
Statement (A) : Total surface area of the cylinder having radius of the base 14 cm and height 30 cm is 3872 cm².
Statement (B): If r be the radius and ‘h’ be the height of the cylinder, then total surface area= (2πrh + 2πr²)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true, iv) Both A and B are false.
Answer:
i) Both A and B are true.
Explanation:
A and B both are correct and B is the correct explanation of the A.
Total surface area = 2πrh × 2πr²
= 2πrh × 2πr²
= 2πr(h + r)
= 2 × \(\frac{22}{7}\) × 14 (30 + 14)
= 88 (44) = 3872 cm²
Hence, (i) is the correct’option,

Question 132.
Statement (A): If the height of a cone is 24 cm and diameter of the base is 14 cm, then the slant height of the cone is 15 cm.
Statement (B) : If r be the radius and h the slant height of the cone, then slant
height = \(\sqrt{\mathrm{h}^{2}+\mathrm{r}^{2}}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
iii) A is false, B is true.
Explanation:
A is incorrect here, but B is correct.
Slant height = \(\sqrt{\left(\frac{14}{2}\right)^{2}+(24)^{2}}\)
= \(\sqrt{49+576}\)
= \(\sqrt{625}\) = 25
Hence, (iii) is the correct option.

Question 133.
Statement (A): If the radius of a cone is halved and volume is not changed, then height remains same.
Statement (B): If the radius of a cone is halved and volume is not changed then height must become four times of the original height.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
iii) A is false, B is true.
Explanation:
A is incorrect and B is correct.

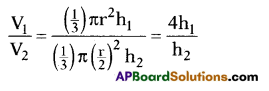
as V₁ = V₂
∴ 4h₁ = h₂
Hence, (iii) is the correct option.

Question 134.
Statement (A): If a ball in the shape of a sphere has a surface area of 221.76 cm2, then its diameter is 8.4 cm.
Statement (B) : If the radius of the sphere be r, then surface area S = 4πr²,
i.e., r = \(\frac{1}{2} \sqrt{\frac{\mathrm{s}}{\pi}}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
i) Both A and B are true.

Question 135.
Statement (A) : Number of spherical balls that can be made out of a solid cube of lead whose edge is 44 cm, each ball being 4 cm in diameter is 2541.
Statement (B) : Number of balls = \(\frac{\text { Volume of one ball }}{\text { Volume of lead }}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
ii) A is true, B is false.

Question 136.
Statement (A) : If the base area and height of a prism be 25 cm² and 6 cm respectively, then its volume is 150 cm³.
Statement (B): Volume of a pyramid = \(\frac{\text { Basearea } \times \text { height }}{3}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
i) Both A and B are true.
Explanation:
A and B both are correct, but B is not the correct explanation of the A.
Volume of a prism = Base area × height
= 25 × 6 = 150 cm₃
Hence, (i) is the correct option.

❖ Read the below passages and answer to the following questions.
A tent is in the form of a right circular cylinder, surmounted by a cone. The diameter of the cylinder is 24 m. The height of the cylindrical portion is 11m, while the vertex of the cone is 16 m above the ground.

Question 137.
The curved surface area of the cylindrical portion is
Answer:
(264π) m²
Explanation:
R = Radius = \(\frac{24}{2}\) = 12 m.
H = Height = 11 m.
Curved surface area of the cylindrical portion = 2πRH
= 2π(12)(11) = (264 π)m₂.

Question 138.
The slant height of the cone is
Answer:
13 m
Explanation:

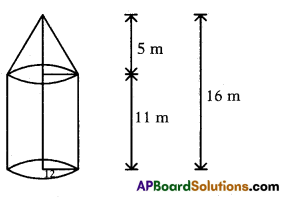
h = Height of the cylindrical portion
= 16 – 11 = 5m .
Slant height,
L = \(\sqrt{h^{2}+R^{2}}\) =\(\sqrt{25+144}\) = 13 m

Question 139.
The area of the canvas required for the tent is
Answer:
1320 m²
Latha said “Cuboid is one of right prism”.
Explanation:
Area of canvas required for the tent = Curved surface area of the cylindrical portion + Curved surface area of the cone
Surface area = 2πrh + πrl
= πr(2h + l)
= \(\frac{22}{7}\) × 12 (22 + 13)
\(\frac{264}{7}\) (22 + 13)
\(\frac{264}{7}\) × 35
= 132 cm ₂

Question 140.
Is Latha right or wrong?
Answer:
Yes.

Question 141.
Which concept is used from your text-book to support Latha?
Answer:
Mensuration
A toy is in the form of a cone mounted on a hemisphere. The radius of the base and the height of the cone are 7 Cm and 8 cm respectively.

Question 142.
What is the common measure in the toy of two situations?
Answer:
Radius of hemisphere = Radius of cone.

Question 143.
Find the slant height of cone.
Answer:
l = \(\sqrt{113} \mathrm{~cm}\)cm

Question 144.
For finding surface area of the toy, what are required?
Answer:
C.S. A of cone and surface area of hemisphere.
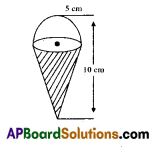
An ice-cream cone full of ice-cream having radius 5 cm and height 10 cm.

Question 145.
Write the combinations of given solid figure.
Answer:
Cone + hemisphere

Question 146.
What are the radii of cone and hemisphere?
Answer:
Hemisphere radius = 5 cm and cone radius = 5 cm

Question 147.
How much the volume of ice-cream contained in conical part?
Answer:
V = 130.95 cm³

Question 148.
How much the volume of ice-cream contained in hemisphere part?
261.90 cm³

Question 149.
For figure shown, match the column.

Answer:
A – (ii), B – (i), C – (iii), D – (iv)

Question 150.
For a wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in fig. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm.

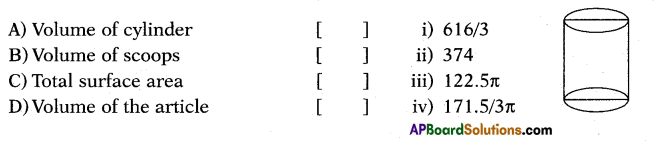
Answer:
A – (iii), B – (iv), C – (ii), D – (i)

Question 151.
From a solid cylinder of height 2.4 cm and diameter 1.4 cm., a conical cavity of the same height and some diameter is followed out them match the column.

Answer:
A – (ii), B – (i), C – (iii), D – (iv)

Question 152.
The capacity of an oil drum is 10litres then what is its volume? (in cm³)
AP LModel Paper I
Answer:
10,000 cm³

Question 153.
Food grains are to be stored in containers of the same base length and height. Which type of containers are required less in number to store a fixed quantity of grains?
i) Right Circular Cylinder
ii) Cube
iii) Right Circular Cone
Answer:
ii) Cube

Question 154.
An open water tank is in the shape of a Cuboid with outer dimensions – length V units, breadth ‘y’ units and height ‘z’ units. If the thickness of the wall is ‘a’ units, express the inner dimensions.
Solution:
Inner Dimensions :
Length = x – a – a = x – 2a units
(both side wall thickness reduced).
Breadth = y – a – a = y – 2a units
(both side wall thickness reduced).
Height = z – a units (as open from top so only bottom thickness reduced)

Question 155.
Choose the correct answer satisfying the following statements.
Statement (A) : The ratio of volumes of cone and cylinder of same base and same height is 3 : 1 Statement (B) : The ratio of volumes of sphere and cone of same radius and same height is 2 : 1
i) Both A and B are true
ii) A is true, B is false
iii) A is false, B is true .
iv) Both A and B are false
Answer:
iv) Both A and B are false