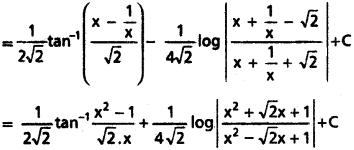Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Integration Solutions Exercise 6(d) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2B Integration Solutions Exercise 6(d)
I. Evaluate the following integrals.
Question 1.
∫\(\frac{dx}{\sqrt{2x-3x^2+1}}\)
Solution:

Question 2.
∫\(\frac{\sin \theta}{\sqrt{2-\cos^2 \theta}}\)dθ
Solution:

Question 3.
∫\(\frac{\cos x}{\sin^2 x+4sin x+5}\)dx
Solution:
t = sin x ⇒ dt = cos x dx
I = ∫\(\frac{dt}{t^2+4t+5}\) = ∫\(\frac{dt}{(t+2)^2+1}\)
= tan-1(t + 2) + C
= tan-1(sin x + 2) + C
![]()
Question 4.
∫\(\frac{dx}{1+\cos^2 x}\)
Solution:
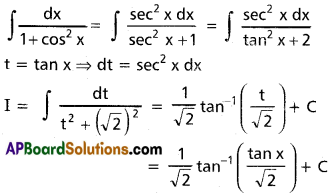
Question 5.
∫\(\frac{dx}{2\sin^2 x+3\cos^2 x}\)
Solution:

Question 6.
∫\(\frac{1}{1+\tan x}\)dx
Solution:
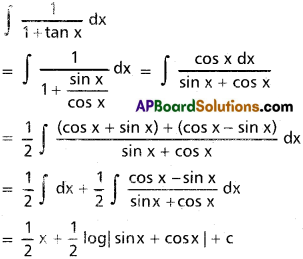
Question 7.
∫\(\frac{1}{1-\cot x}\)dx
Solution:
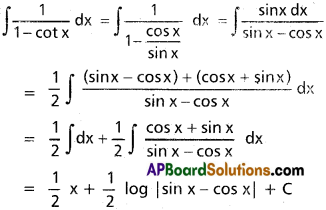
II. Evaluate the following integrals.
Question 1.
∫\(\sqrt{1+3x-x^2}\)dx
Solution:

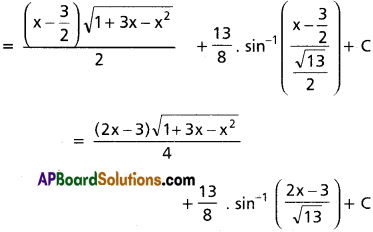
Question 2.
∫\(\frac{9\cos x-\sin x}{4\sin x+5\cos x}\)dx
Solution:
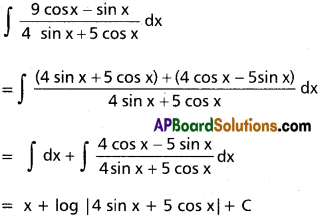
Question 3.
∫\(\frac{2\cos x+3\sin x}{4\cos x+5\sin x}\)dx
Solution:
Let 2 cos c + 3 sin x = A(4 cos x + 5 sin x) + B(-4 sin x + 5 cos x)
Equating the co-efficient of sin x and cos x,
we get
4A + 5B = 2
5A – 4B = 3
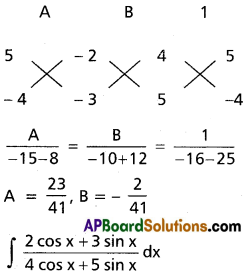
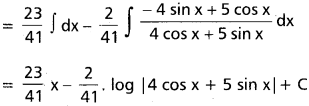
![]()
Question 4.
∫\(\frac{1}{1+\sin x+\cos x}\)dx
Solution:

Question 5.
∫\(\frac{1}{3x^2+x+1}\)dx
Solution:

Question 6.
∫\(\frac{dx}{\sqrt{5-2x^2+4x}}\)
Solution:
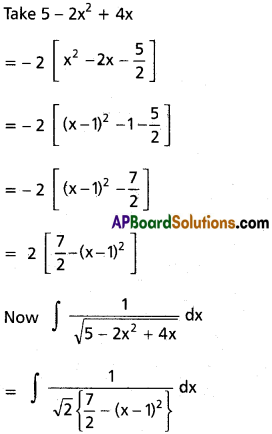

III. Evaluate the following integrals.
Question 1.
∫\(\frac{x+1}{\sqrt{x^2-x+1}}\)
Solution:

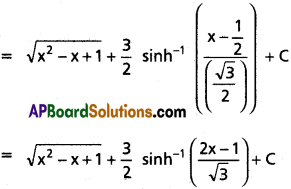
Question 2.
∫(6x + 5)\(\sqrt{6-2x^2+x}\)dx
Solution:
Let 6x + 5 = A(1 – 4x) + B
Equating the constants
A + B = 5
B = 5 – A = 5 + \(\frac{3}{2}\) = \(\frac{13}{2}\)
∫(6x + 5)\(\sqrt{6-2x^2+x}\)dx


Question 3.
∫\(\frac{dx}{4+5\sin x}\)
Solution:
t = tan \(\frac{x}{2}\) ⇒ dt = sec² \(\frac{x}{2}\) . \(\frac{1}{2}\)dx

![]()
Question 4.
∫\(\frac{1}{2-3\cos 2x}\)dx
Solution:
t = tan x ⇒ dt = sec² x dx
= (1 + tan² x)dx
= (1 +t²)dx
dx = \(\frac{dt}{1+t^2}\)

Question 5.
∫x\(\sqrt{1+x-x^2}\)dx
Solution:
Let x = A(1 – 2x) + B
Equating the coefficients of x
1 = -2 A ⇒ A = –\(\frac{1}{2}\)
Equating the constants
0 = A + B ⇒ B = -A = \(\frac{1}{2}\)
∫x\(\sqrt{1+x-x^2}\)dx
= –\(\frac{1}{2}\)∫(1 – 2x)\(\sqrt{1+x-x^2}\)dx + \(\frac{1}{2}\)∫\(\sqrt{1+x-x^2}\)dx

Question 6.
∫\(\frac{dx}{(1+x)\sqrt{3+2x-x^2}}\)
Solution:


Question 7.
∫\(\frac{dx}{4\cos x+3\sin x}\)
Solution:
Let t = tan\(\frac{x}{2}\) so that dx = \(\frac{2dt}{1+t^2}\)

Question 8.
∫\(\frac{1}{\sin x+\sqrt{3} \cos x}\)dx
Solution:
Let t = tan \(\frac{x}{2}\) so that dx = \(\frac{2dt}{1+t^2}\)
sin x = \(\frac{2t}{1+t^2}\), cos x = \(\frac{1-t^2}{1+t^2}\)
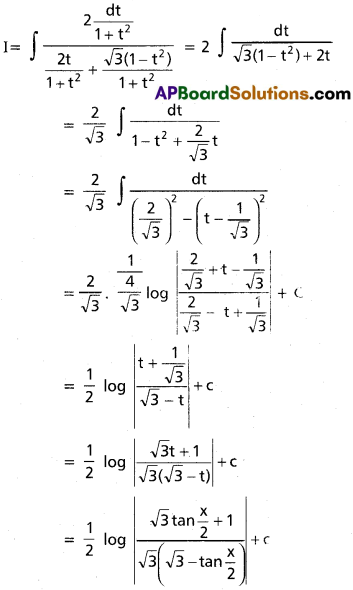
![]()
Question 9.
∫\(\frac{dx}{5+4\cos 2x}\).
Solution:
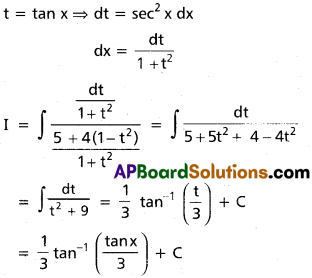
Question 10.
∫\(\frac{2\sin x+3\cos x+4}{3\sin x+4\cos x+5}\)dx.
Solution:
Let 2 sin x + 3 cos x + 4
= A(3 sin x + 4 cos x + 5) + 3(3 cos x – 4 sin x) + C
Equating the co-efficient of
sin x, we get 3A – 4B = 2
cos x, we get 4A + 3B = 3
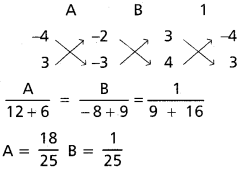
Equating the constants
4 = 5A + C
C = 4 – 5A = 4 – 5.\(\frac{18}{25}\) = \(\frac{2}{5}\)

Substituting in (1)
I = \(\frac{18}{25}\). x + \(\frac{1}{25}\) log|3 sin x + 4 cos x + 5| – \(\frac{4}{5\left(3+\tan \frac{x}{2}\right)}\) + C
Question 11.
∫\(\sqrt{\frac{5-x}{x-2}}\) dx on (2, 5).
Solution:

Let 5 – x = A. \(\frac{d}{dx}\)(7x – 10 – x²) + B
⇒ 5 – x = A(7 – 2x) + B
Equating coffs. of like terms
-2A = -1 ⇒ A = \(\frac{1}{2}\)
7A + B = 5
7(+\(\frac{1}{2}\)) + B = 5 ⇒ B = 5 – \(\frac{7}{2}\) = \(\frac{3}{2}\)
∴ 5 – x = \(\frac{1}{2}\)(7 – 2x) + \(\frac{3}{2}\)


Question 12.
∫\(\sqrt{\frac{1+x}{1-x}}\) dx on (-1, 1).
Solution:

![]()
Question 13.
∫\(\frac{dx}{(1 – x)\sqrt{3-2x+x^2}}\) on (-1, 3).
Solution:
Put 1 – x = \(\frac{1}{1}\) ⇒ 1 – \(\frac{1}{1}\) = x\(\frac{1}{1-x}\) = t
dx = \(\frac{1}{t^2}\)dt
3 – 2x – x² = 3 – 2(\(\frac{1-1}{1}\)) – (\(\frac{1-1}{1}\))²

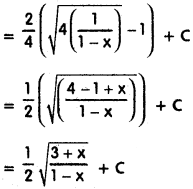
Question 14.
∫\(\frac{dx}{(x + 2)\sqrt{x+1}}\) on (-1, ∞).
Solution:
Put = x + 1 = t² ⇒ dx = 2t dt and
x + 2 = 1 + t²
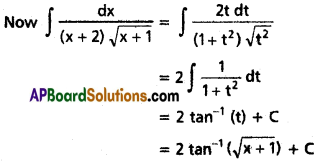
Question 15.
∫\(\frac{dx}{(2x + 3)\sqrt{x+2}}\) on I ⊂ (-2, ∞)\{\(\frac{-3}{2}\)}.
Solution:
Put x + 2 = t² ⇒ dx = 2t dt and
2x + 3 = 2(t² – 2) + 3 = 2t² – 1

Question 16.
∫\(\frac{1}{(1+\sqrt{x}) \sqrt{x-x^2}}\)dx on (0, 1).
Solution:


Question 17.
∫\(\frac{dx}{(x + 1)\sqrt{2x^2+3x+1}}\) on
Solution:

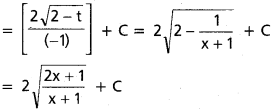
Question 18.
∫\(\sqrt{e^x-4}\) dx on [loge 4, ∞]
Solution:
Put ex – 4 = t² ⇒ ex dx = 2t dt

Question 19.
∫\(\sqrt{1+\sec x}\) dx on [(2n – \(\frac{1}{2}\))π – (2n + \(\frac{1}{2}\))π], (n ∈ Z).
Solution:
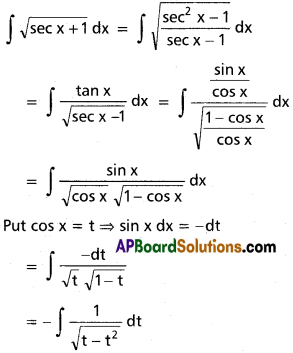
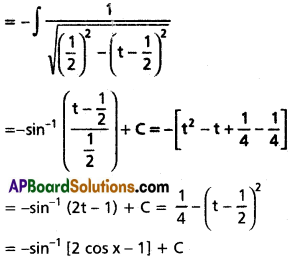
![]()
Question 20.
∫\(\frac{dx}{1+x^4}\) on R.
Solution: