Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Definite Integrals Solutions Exercise 7(d) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2B Definite Integrals Solutions Exercise 7(d)
I.
Question 1.
Fine the area of the region enclosed by the given curves.
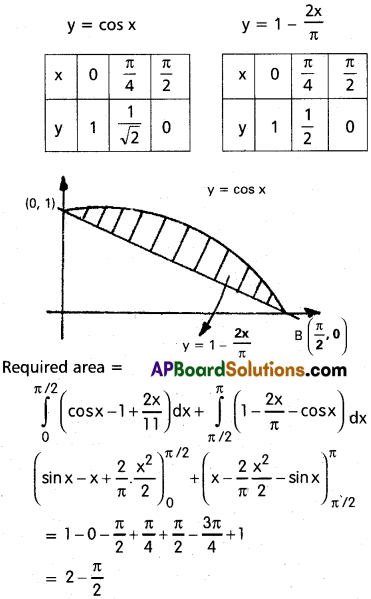
i) y = cos x, y = 1 – \(\frac{2x}{\pi}\)
Solution:
Equations of the given curves are
y = cos x ………….. (1)
y = 1 – \(\frac{2x}{\pi}\) ………….. (2)
Eliminating y from eq’s (1) and (2)
cos x = 1 – \(\frac{2x}{\pi}\)
When x = \(\frac{\pi}{2}\), cos x = cos\(\frac{\pi}{2}\) = 0
1 – \(\frac{2}{\pi}\), x = \(\frac{2}{\pi}\) . \(\frac{\pi}{2}\) = 1 – 1 = 0
When x = 0, cos x = cos 0 = 1
1 – \(\frac{2x}{\pi}\) = 1 – 0 = 1
∴ Point of intersection are A = (\(\frac{\pi}{2}\), 0) B = [π – 1]
Question 2.
y =cos x, y = sin 2x, x = 0, x = \(\frac{\pi}{2}\).
Solution:
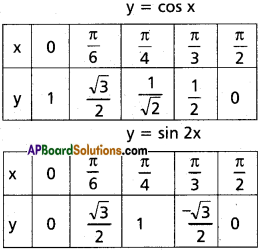
![]()
Question 3.
y = x³ + 3, y = 0, x = -1, x = 2.
Solution:
Required area PABQ

Question 4.
y = ex, y = x, x = 0, x = 1.
Solution:
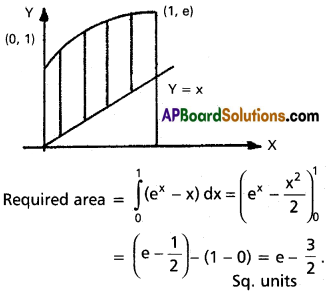
Question 5.
y = sin x, y = cos x; x = 0, x = \(\frac{\pi}{2}\).
Solution:
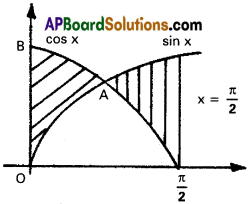
Between 0 and \(\frac{\pi}{4}\).
cos x > sin x
Between \(\frac{\pi}{4}\) and \(\frac{\pi}{2}\)
cos x < sin x
Required area
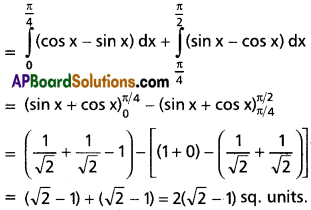
Question 6.
x = 4 – y², x = 0.
Solution:
The given parabola x = 4 – y² meets, the x – axis at A(4, 0) and Y – axis at P(0, 2) and Q(0, -2).
The parabola is symmetrical about X – axis
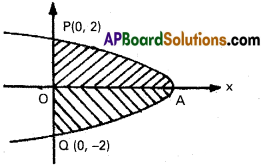
Required area = 2 Area of OAP
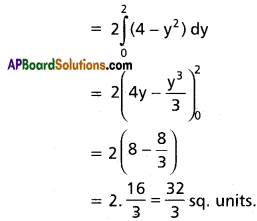
Question 7.
Find the area enclosed with in the curve |x| + |y| = 1
Solution:
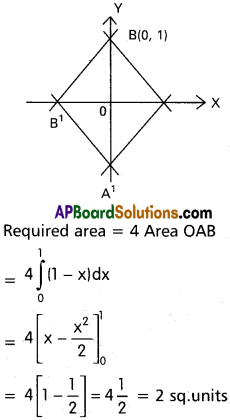
II.
Question 1.
x = 2 – 5y – 3y², x = 0.
Solution:
Solving the equation of given curves
2 – 5y – 3y² = 0
3y² + 5y – 2 = 0
(y + 2)(3y – 1) = 0 y = -2 or \(\frac{1}{3}\)

Question 2.
x² = 4y, x = 2, y = 0.
Solution:
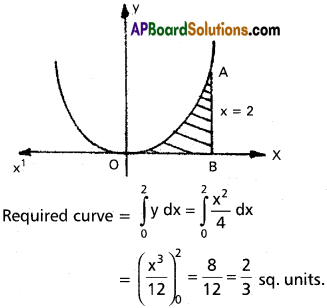
Question 3.
y² = 3x, x = 3.
Solution:
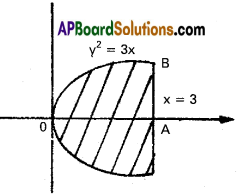
The parabola is symmetrical about X – axis
Required area = 2\(\int_0^3\)√3. √x dx
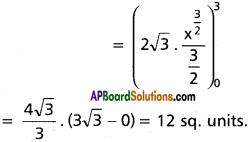
Question 4.
y = x², y = 2x.
Solution:
Given equation are y = x² ………….. (1)
y = 2x …………. (2)
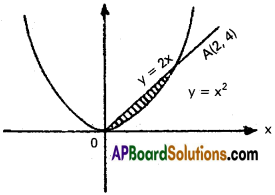
Eliminating y, we get x² = 2x
x² – 2x = 0
x(x – 2) = 0
x = 0 or x = 2
y = 0, or y = 4
Point of intersection are O(0, 0), A(2, 4)
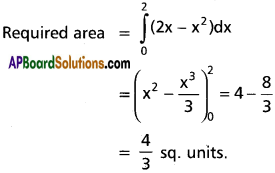
Question 5.
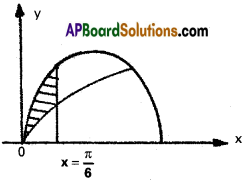
y = sin 2x, y = √3 sin x, x = 0, x = \(\frac{\pi}{6}\).
Solution:
Given equation are y = sin 2x ………… (1)
y = √3 sin x …………. (2)
sin 2x = √3 sin x
2 sin x. cos x = √3 sin x
sin x = 0 or 2 cos x = \(\frac{\sqrt{3}}{2}\)
x = 0, cos x = \(\frac{\sqrt{3}}{2}\) ⇒ x = \(\frac{\pi}{6}\)
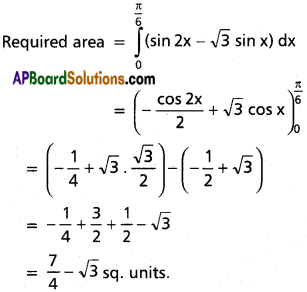
![]()
Question 6.
y = x², y = x³.
Solution:
Given equations are y = x² ………….. (1)
y = x³ ………. (2)
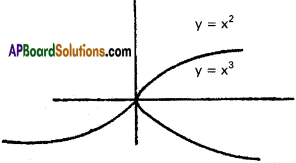
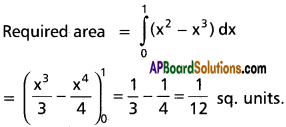
From equation (1) and (2) x² = x³
x³ – x² = 0
x²(x – 1) = 0
x = 0 or 1
Question 7.
y = 4x – x², y = 5 – 2x
Solution:
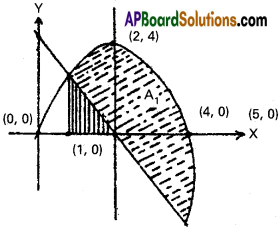
y = 4x – x² ………… (i)
y = 5 – 2x …………..(ii)
y = -([x – 2]²) = 4
y – 4 = -(x – 2)²
Solving equations (i) and (ii) we get
4x – x² = 5 – 2x
x² – 6x + 5 = 0
(x – 5)(x – 1 ) = 0
x = 1, 5

Question 8.
Find the area in Sq. units bounded by the x – axis, part of the curve y = 1 + \(\frac{8}{x^2}\) and the ordinates x = 2 and x = 4.
Solution:
Given equations y = 1 + \(\frac{8}{x^2}\)
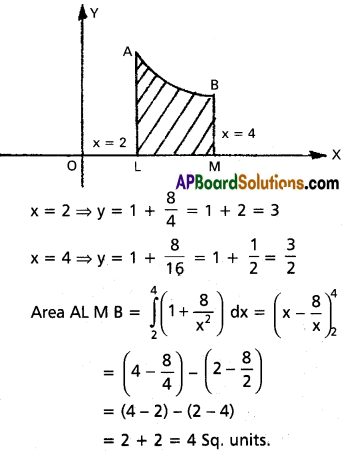
Question 9.
Find the area of the region bounded by the parabolas y² = 4x and x² = 4y.
Solution:
Equations of the given curve are
y² = 4x
x² = 4y
(\(\frac{x^2}{4}\))² = 4x
\(\frac{x^4}{16}\) = 4x
x4 = 64x ⇒ x4 = 0 or x³ = 64, x = 4
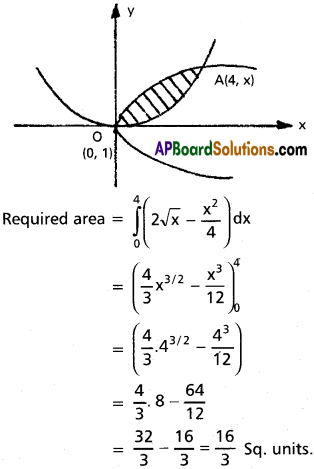
Question 10.
Find the area bounded by the curve y = lnx the X – axis and the straight line x = e.
Solution:
Equation of the curve is y = lnx
x = 1 ⇒ y = 0
The curve y = lnx meets
X – axis at C(1, 0)
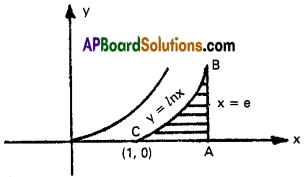
Required area = \(\int_1^e\)lnx dx
= (x.lnx)e1 – \(\int_1^e\)x.\(\frac{1}{x}\) dx
= (e.ln e – 1.ln 1) – (x)e1
= e – (e – 1)
= e – e + 1 = 1 Sq.unit.
III.
Question 1.
y = x² + 1, y = 2x – 2, x = -1, x = 2.
Solution:
Equation of the curve are
y = x² + 1 …………. (1)
y = 2x – 2 ………….. (2)
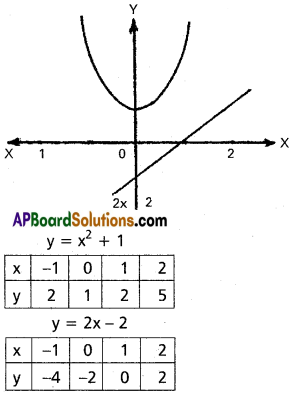
Area between the given curves

Question 2.
y² = 4x, y² = 4(4 – x).
Solution:
Equations of the curve are y² = 4x ………… (1)
y² = 4(4 – x) …………. (2)
Eliminating y, we get
4x = 4(4 – x)
2x = 4 ⇒ x = 2
Substituting in equation (1), y² = 8
y = ± 2√2
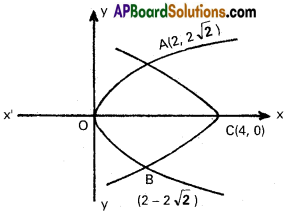
Points of intersection are
A(2, 2√2), B(2, -2√2)
Required area is symmetrical about X – axis
Area OACB

Question 3.
y = 2 – x², y = x².
Solution:
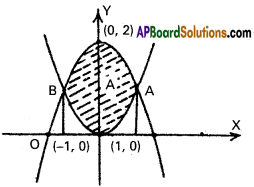
y = 2 – x² …………. (1)
y = x² …………. (2)
x² = -(y – 2)
From equation (2)
2 – x² = x²
2 = 2x² or x² = 1
x = ±1
Area bounded by two curve be
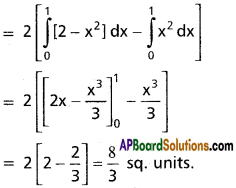
Question 4.
Show that the area enclosed between the curve y² = 12(x + 3) and y² = 20(5 – x) is 64\(\sqrt{\frac{5}{3}}\).
Solution:
Equation of the curve are
y² = 12(x + 3) ……….. (1)
y² = 20(5 – x) ……….. (2)
Eliminating y
12(x + 3) = 20(5 – x)
3x + 9 = 25 – 5x
8x = 16
x = 2
y² = 12(2 + 3) = 60
y = √60 = ±2√15
Points of intersection are B’ (2, 2√15)
B’ (+2, -2√15)
The required area is symmetrical about X – axis
Area ABCB’

![]()
Question 5.
Find the area of the region {(x, y)/x² – x – 1 ≤ y ≤ -1}
Solution:
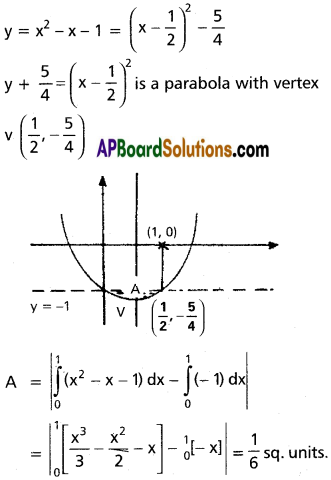
Question 6.
The circle x² + y² = 8 is divided into two parts by the parabola 2y = x². Find the area of both the parts.
Solution:
Equations of the curves are
x² + y² = 8 ………… (1)
2y = x² ………… (2)
Eliminating y between equations (1) and (2)
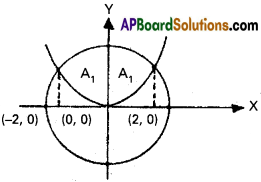
Let x² = t
4t + t² = 32
t² + 4t – 32 = 0
(t + 8)(t – 4) = 0
t = -8 (not possible) x² = 4 ⇒ x = ±2
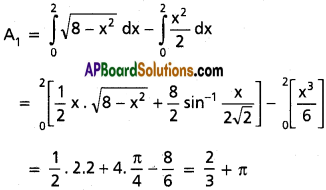
As curve is symmetric about Y – axis, total area be
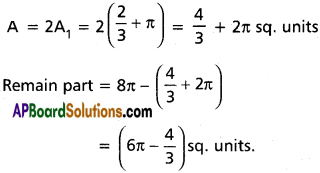
Question 7.
Show that the area of the region bounded \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 (ellipse) is π ab. also deduce the area of the cricle x² + y² = a².
Solution:
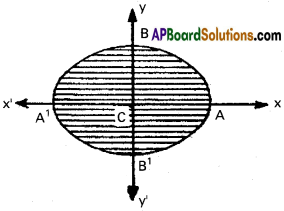
The ellipse is symmetrical about X and Y axis
Area of the ellipse = 4 Area of CAB
= 4.\(\frac{\pi}{4}\) ab
Equation of elliple = \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
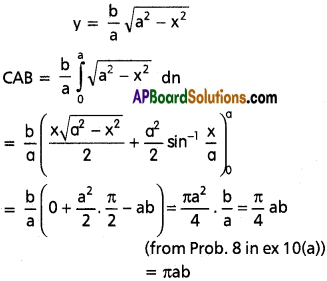
Substituting b = a, we get the circle
x² + y² = a²
Area of the circle = πa(a) = πa² sq. units.
Question 8.
Find the area of region enclosed by the curves y = sin πx, y = x² – x, x = 2.
Solution:
Required area
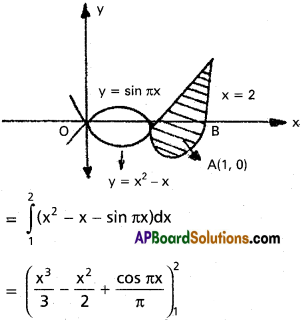
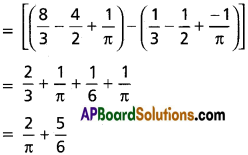
Question 9.
Let AOB be the positive quadrant of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 with OA = a, OB = b. Then show that the area bounded the chord AB and the arc AB of the elliple is \(\frac{(\pi-2) a b}{4}\).
Solution:
Let OA = a, OB = b
Equation of AB is \(\frac{x}{a}+\frac{y}{b}\) = 1
\(\frac{y}{b}\) = 1 – \(\frac{x}{a}\)
y = b(1 – \(\frac{x}{a}\))


![]()
Question 10.
Prove that curves y² = 4x and x² = 4y divide the area of the square bounded by the lines x = 0, x = 4, y = 4 and x = 0 into three equal parts.
Solution:
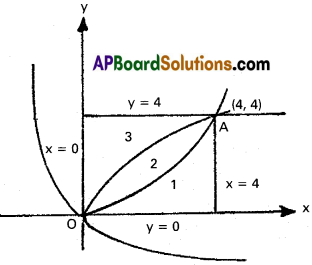
The given equations are y² = 4x …………. (1)
x² = 4y …………. (2)
The points of intersection are O(0, 0) A(4, 4)
