Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Probability Solutions Exercise 9(b) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2A Probability Solutions Exercise 9(b)
I.
Question 1.
If 4 fair coins are tossed simultaneously, then find the probability that 2 heads and 2 tails appear.
Solution:
4 coins are tossed simultaneously.
Total number of ways = 24 = 16
n(S) = 16
From 4 heads we must get 2 heads.
Number of ways of getting 2 heads = 4C2
= \(\frac{4.3}{1.2}\)
= 6
∴ n(E) = 6
P(E) = \(\frac{n(E)}{n(S)}=\frac{6}{16}=\frac{3}{8}\)
∴ Probability of getting 2 heads and 2 tails = \(\frac{3}{8}\)
Question 2.
Find the probability that a non-leap year contains
(i) 53 Sundays
(ii) 52 Sundays only
Solution:
A non-leap year contains 365 days 52 weeks and 1 day more.
(i) We get 53 Sundays when the remaining day is Sunday.
Number of days in the week = 7
∴ n(S) = 7
The number of ways getting 53 Sundays.
n(E) = 1
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{1}{7}\)
∴ Probability of getting 53 Sundays = \(\frac{1}{7}\)
(ii) Probability of getting 52 Sundays
P(\((\overline{\mathrm{E}})\)) = 1 – P(E)
= 1 – \(\frac{1}{7}\)
= \(\frac{6}{7}\)
![]()
Question 3.
Two dice are rolled, what is the probability that none of the dice shows the number 2?
Solution:
The random experiment is rolling 2 dice.
n(S) = 62 = 36
Let E be the event of not getting 2
n(E) = 5 × 5 = 25
∴ P(E) = \(\frac{\mathrm{n}(E)}{\mathrm{n}(s)}=\frac{25}{36}\)
Question 4.
In an experiment of drawing a card at random from a pack, the event of getting a spade is denoted by A, and getting a pictured card (King, Queen, or Jack) is denoted by B. Find the probabilities of A, B, A ∩ B, and A ∪ B.
Solution:
A is the event of getting a spade from the pack
∴ P(A) = \(\frac{13}{52}=\frac{1}{4}\)
B is the event of getting a picture card
P(B) = \(\frac{4 \times 3}{52}=\frac{3}{13}\)
A ∩ B is the event of getting a picture card in spades.
n(A ∩ B) = 3, n(s) = 52
P(A ∩ B) = \(\frac{3}{52}\)
A ∪ B is the event of getting a spade or a picture card.
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{1}{4}+\frac{3}{13}-\frac{3}{52}\)
= \(\frac{13+12-3}{52}\)
= \(\frac{11}{26}\)
Question 5.
In a class of 60 boys and 20 girls, half of the boys and half of the girls know cricket. Find the probability of the event that a person selected from the class is either a boy or a girl who knows cricket.
Solution:
Let A be the event that the selected person is a boy and B be the event that the selected person knows a cricket when a person is selected from the class and S be the sample space.
Now, n(S) = 80C1 = 80
n(A) = 60C1 = 60
n(B) = 40C1 = 40
n(A ∩ B) = 30C1 = 30
∴ P(A) = \(\frac{60}{80}\), P(B) = \(\frac{40}{80}\), P(A ∩ B) = \(\frac{30}{80}\)
∴ P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{60}{80}+\frac{40}{80}-\frac{30}{80}\)
= \(\frac{70}{80}\)
= \(\frac{7}{8}\)
Question 6.
For any two events A and B, show that P(AC ∩ BC) = 1 + P(A ∩ B) – P(A) – P(B).
Solution:
AC ∩ BC = \(\overline{A \cup B}\)
P(AC ∩ BC) = P(\(\overline{A \cup B}\))
= 1 – P(A ∪ B)
= 1 – [P(A) + P(B) – P(A ∩ B)]
= 1 + P(A ∩ B) – P(A) – P(B)
![]()
Question 7.
Two persons A and B are rolling die on the condition that the person who gets 3 will win the game. If A starts the game, then find the probabilities of A and B respectively to win the game.
Solution:
p = Probability of getting 3 = \(\frac{1}{6}\)
q = 1 – p
= 1 – \(\frac{1}{6}\)
= \(\frac{5}{6}\)
Probability success (p) = \(\frac{1}{6}\)
Probability of failure (q) = \(\frac{5}{6}\)
A may win the game either in I trial or in trial or in V trial etc.
Probability of A win = p + q . q . p + q . q . q . q . p + ……..

Question 8.
A, B, C are 3 newspapers from a city. 20% of the population read A, 16% read B, 14% read C, 8% both A and B, 5% both A and C, 4% both B and C, and 2% all the three. Find the percentage of the population who read atleast one newspaper.
Solution:
Given P(A) = \(\frac{20}{100}\) = 0.2
P(B) = \(\frac{16}{100}\) = 0.16
P(C) = \(\frac{14}{100}\) = 0.14
P(A ∩ B) = \(\frac{8}{100}\) = 0.08
P(B ∩ C) = \(\frac{4}{100}\) = 0.04
P(A ∩ C) = \(\frac{5}{100}\) = 0.05
P(A ∩ B ∩ C) = \(\frac{2}{100}\) = 0.02
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C)
= 0.2 + 0.16 + 0.14 – 0.08 – 0.04 – 0.05 + 0.02
= 0.52 – 0.17
= 0.35
Percentage of population who read atleast one newspaper = 0.35 × 100 = 35%
Question 9.
If one ticket is randomly selected from tickets numbered 1 to 30. Then find the probability that the number on the ticket is
(i) a multiple of 5 or 7
(ii) a multiple of 3 or 5
Solution:
(i) Number of ways drawing one ticket = n(S) = 30C1 = 30
Suppose A is the event of getting a multiple of 5 and B is the event of getting a multiple of 7.
A = {5, 10, 15, 20, 25, 30}
B = {7, 14, 21, 28}
A ∩ B = φ ⇒ A and B are mutually exclusive
P(A ∪ B) = P(A) + P(B)
= \(\frac{6}{30}+\frac{4}{30}\)
= \(\frac{1}{3}\)
Probability of getting a multiple of 5 or 7 = \(\frac{1}{3}\)
(ii) Suppose A is the event of getting a multiple of 3 and B is the event of getting a multiple of 5.
A = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
B = {5, 10, 15, 20, 25, 30}
A ∩ B = {15, 30}
P(A) = \(\frac{10}{30}\)
P(B) = \(\frac{6}{30}\)
P(A ∩ B) = \(\frac{2}{30}\)
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{10}{30}+\frac{6}{30}-\frac{2}{30}\)
= \(\frac{14}{30}\)
= \(\frac{7}{15}\)
Probability of getting a multiple of 3 or 5 = \(\frac{7}{15}\)
Question 10.
If two numbers are selected randomly from 20 consecutive natural numbers, find the probability that the sum of the two numbers is (i) an even number (ii) an odd number.
Solution:
(i) Let A be the event that the sum of the numbers is even when two numbers are selected out of 20 consecutive natural numbers.
In 20 consecutive natural numbers, we have 10 odd and 10 even natural numbers.
∵ The sum of two odd natural numbers is an even number and the sum of two even natural numbers is also an even number
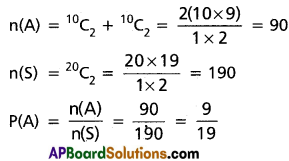
(ii) Probability that the sum of two numbers is an odd number
P(\(\overline{\mathrm{A}}\)) = 1 – P(A)
= 1 – \(\frac{9}{19}\)
= \(\frac{10}{19}\)
![]()
Question 11.
A game consists of tossing a coin 3 times and noting its outcome. A boy wins if all tosses give the same outcome and lose otherwise. Find the probability that the boy loses the game.
Solution:
Let A be the event that the boy wins the game getting the same outcome when a coin is tossed 3 times and S be the sample space.
∴ n(S) = 23 = 8
A = {HHH, TTT}
n(A) = 2
P(A) = \(\frac{n(A)}{n(S)}=\frac{2}{8}=\frac{1}{4}\)
∴ The probability that the boy loses the game = P(\(\overline{\mathrm{A}}\))
= 1 – P(A)
= 1 – \(\frac{1}{4}\)
= \(\frac{3}{4}\)
Question 12.
If E1, E2 are two events with E1 ∩ E2 = φ then show that \(P\left(E_1^c \cap E_2^c\right)=P\left(E_1^c\right)-P\left(E_2\right)\)
Solution:
Given E1 ∩ E2 = φ
∴ P(E1 ∩ E2) = 0
\(P\left(E_1^c \cap E_2^c\right)=P\left(\overline{E_1 \cup E_2}\right)\)
= 1 – P(E1 ∪ E2)
= 1 – [P(E1) + P(E2) – P(E1 ∩ E2)]
= 1 – P(E1) – P(E2) + P(E1 ∩ E2)
= \(P\left(E_1^c\right)\) – P(E2) + 0
∴ \(P\left(E_1^c \cap E_2^c\right)=P\left(E_1^c\right)-P\left(E_2\right)\)
II.
Question 1.
A pair of dice rolled 24 times. A person wins by not getting a pair of 6’s on any of the 24 rolls. What is the probability of his winning?
Solution:
Random experiment is tossing two dice 24 times = 36 × 36 × ……. 36 = (36)24
∴ n(S) = (36)24
Let A be the event of not getting a pair of 6’s on any of the 24 rolls.
∴ number of ways favourable to an event A = 35 × 35 × ……. × 35 = (35)24
n(A) = (35)24
∴ P(A) = \(\frac{(35)^{24}}{(36)^{24}}=\left(\frac{35}{36}\right)^{24}\)
Question 2.
If P is a probability function, then show that for any two events A and B.
P(A ∩ B) ≤ P(A) ≤ P(A ∪ B) ≤ P(A) + P(B)
Solution:
For any sets A, B we have
A ∩ B ≤ A ≤ A ∪ B
P(A ∩ B) ≤ P(A) ≤ P(A ∪ B)
By Addition theorem of probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B) ≤ P(A) + P(B) ……….(2)
From (1), (2) we get
P(A ∩ B) ≤ P(A) ≤ P(A ∪ B) ≤ P(A) + P(B)
![]()
Question 3.
In a box containing 15 bulbs, 5 are defective. If 5 bulbs are selected at random from the box, find the probability of the event, that
(i) None of them is defective
(ii) Only one of them is defective
(iii) Atleast one of them is defective
Solution:
Out of 15 bulbs, 5 are defective
probability of selecting a defective bulb = P
= \(\frac{5}{15}\)
= \(\frac{1}{3}\)
We are selecting 5 bulbs
n(S) = 15C5
(i) None of them is defective.
All 5 bulbs must be selected from 10 good bulbs. This can be done in 10C5 ways.
P(A) = \(\frac{{ }^{10} C_5}{{ }^{15} C_5}=\frac{10.9 .8 .7 .6}{15.14 .13 .12 .11}=\frac{12}{143}\)
(ii) Only one of them is defective in 4 good and 1 defective ball.
This can be done in (10C4) (5C1) = \(\frac{10.9 .8 .7}{1.2 \cdot 3.4} \cdot 5\)
= 210 × 5
= 1050
Probability of selecting one defective = \(\frac{1050}{{ }^{15} C_5}\)
= \((1050) \frac{1.2 .3 .4 .5}{15.14 .13 .12 .11}\)
= \(\frac{50}{143}\)
(iii) Probability atleast one of them is defective = P(\(\overline{A}\))
= 1 – P(A)
= 1 – \(\frac{12}{143}\)
= \(\frac{131}{143}\)
Question 4.
A and B are seeking admission into I.I.T. If the probability for A to be selected is 0.5 and that both to be selected is 0.3. Is it possible that the probability of B being selected is 0.9?
Solution:
Given P(A) = 0.5; P(A ∩ B) = 0.3
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.5 + P(B) – 0.3
= 0.2 + P(B)
P(A ∪ B) ≤ 1
0.2 + P(B) ≤ 1
P(B) ≤ 0.8
∴ It is not possible to have P(B) = 0.9
Question 5.
The probability for a contractor to get a road contract is \(\frac{2}{3}\) and to got a building contract is \(\frac{5}{9}\). The probability to get atleast on contract is \(\frac{4}{5}\). Find the probability to get both contracts.
Solution:
Suppose A is the event of getting a road contract
B is the event of getting a building contract
Given P(A) = \(\frac{2}{3}\); P(B) = \(\frac{5}{9}\); P(A ∪ B) = \(\frac{4}{5}\)
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
= \(\frac{2}{3}+\frac{5}{9}-\frac{4}{5}\)
= \(\frac{30+25-36}{45}\)
= \(\frac{19}{45}\)
∴ Probability to get both contracts = \(\frac{19}{45}\)
![]()
Question 6.
In a committee of 25 members, each member is proficient either in Mathematics or Statistics or in both. If 19 of these are proficient in Mathematics, and 16 in Statistics, find the probability that a person selected from the committee is proficient in both.
Solution:
When a person is chosen at random from the academy consisting of 25 members
Let A be the event that the person is proficient in Mathematics
B be the event that the person is proficient in Statistics and
S is the sample space.
Since 19 members are proficient in Mathematics and 16 members are proficient in Statistics.
P(A) = \(\frac{19}{25}\), P(B) = \(\frac{16}{25}\)
Since everyone is either proficient in Mathematics or Statistics or in both
A ∪ B = S
⇒ P(A ∪ B) = P(S)
⇒ P(A) + P(B) – P(A ∩ B) = P(S)
⇒ \(\frac{19}{25}+\frac{16}{25}\) – P(A ∩ B) = 1
⇒ P(A ∩ B) = \(\frac{19}{25}+\frac{16}{25}-1\) = \(\frac{10}{25}\)
∴ P(A ∩ B) = \(\frac{2}{5}\)
Question 7.
A, B, C are three horses in a race. The probability of A winning the race is twice that of B and the probability of B is twice that of C. What are the probabilities of A, B, and C winning the race?
Solution:
Let A, B, C be the events that horses A, B, and C win the race respectively.
Given P(A) = 2P(B), P(B) = 2P(C)
∴ P(A) = 2P(B) = 2[2P(C)] = 4P(C)
Since the horses A, B and C run the race,
A ∪ B ∪ C = S and A, B, C are mutually disjoint.
P(A ∪ B ∪ C) = P(A) + P(B) + P(C)
⇒ P(S) = 4P(C) + 2P(C) + P(C)
⇒ 1 = 7P(C)
⇒ P(C) = \(\frac{1}{7}\)
P(A) = 4P(C) = 4 × \(\frac{1}{7}\) = \(\frac{4}{7}\)
P(B) = 2P(C) = 2 × \(\frac{1}{7}\) = \(\frac{2}{7}\)
∴ P(A) = \(\frac{4}{7}\), P(B) = \(\frac{2}{7}\), P(C) = \(\frac{1}{7}\)
Question 8.
A bag contains 12 two rupee coins, 7 one rupee coins, and 4 half rupee coins. If 3 coins are selected at random find the probability that
(i) The sum of the 3 coins is maximum
(ii) The sum of the 3 coins is minimum
(iii) Each coin is of a different value
Solution:
In the bag, there are 12 two rupees, 7 one rupees, and 4 half rupee coins.
Total number of coins = 12 + 7 + 4 = 23
Number of ways drawing 3 coins 23C3
n(S) = 23C3
(i) We get the maximum amount if the coins are 2 rupee coins.
Number of drawing 3 two rupee coins = 12C3
n(E1) = 12C3
P(E1) = \(\frac{n\left(E_1\right)}{n(S)}=\frac{{ }^{12} C_3}{{ }^{23} C_3}\)
(ii) We get a minimum amount if 3 coins are taken from 4 half rupee coins.
Number of ways of drawing 3 half rupee coins = 4C3
n(E2) = 4C3
P(E2) = \(\frac{n\left(E_2\right)}{n(S)}=\frac{{ }^4 C_3}{{ }^{23} C_3}\)
(iii) Each coin is of different value we must draw one coin each.
This can be done in 12C1, 7C1, 4C1 ways
n(E3) = 12C1 × 7C1 × 4C1 = 12 × 7 × 4
P(E3) = \(\frac{n\left(E_3\right)}{n(S)}=\frac{12 \times 7 \times 4}{{ }^{23} C_3}\)
![]()
Question 9.
The probabilities of three events A, B, C are such that P(A) = 0.3, P(B) = 0.4, P(C) = 0.8, P(A ∩ B) = 0.08, P(A ∩ C) = 0.28, P(A ∩ B ∩ C) = 0.09 and P(A ∪ B ∪ C) ≥ 0.75. Show that P(B ∩ C) lies in the interval [0.23, 0.48]
Solution:
P(A ∪ B ∪ C) ≥ 0.75
0.75 ≤ P(A ∪ B ∪ C) ≤ 1
⇒ 0.75 ≤ P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C) ≤ 1
⇒ 0.75 ≤ 0.3 + 0.4 + 0.8 – 0.08 – 0.28 – P(B ∩ C) + 0.09 ≤ 1
⇒ 0.75 ≤ 1.23 – P(B ∩ C) ≤ 1
⇒ -0.75 ≥ P(B ∩ C) – 1.23 ≥ -1
⇒ 0.48 ≥ P(B ∩ C) ≥ 0.23
⇒ 0.23 ≤ P(B ∩ C) ≤ 0.48
∴ P(B ∩ C) lies in the interval [0.23, 0.48]
Question 10.
The probabilities of three mutually exclusive events are respectively given as \(\frac{1+3 P}{3}, \frac{1-P}{4}, \frac{1-2 P}{2}\). Prove that \(\frac{-1}{3} \leq P \leq \frac{1}{2}\)
Solution:
Three mutually exclusive events probabilities are given.
∴ 0 ≤ \(\frac{1+3 P}{3}\) ≤ 1
⇒ 0 ≤ 1 + 3P ≤ 3
⇒ -1 ≤ P ≤ 2
⇒ \(\frac{-1}{3} \leq P \leq \frac{2}{3}\) …….(1)
Also 0 ≤ \(\frac{1-\mathrm{P}}{4}\) ≤ 1
⇒ 0 ≤ 1 – P ≤ 4
⇒ -1 ≤ -P ≤ 3
⇒ 1 ≥ P ≥ -3
⇒ -3 ≤ P ≤ 1 …….(2)
Also 0 ≤ \(\frac{1-2 P}{2}\) ≤ 1
⇒ 0 ≤ 1 – 2P ≤ 2
⇒ -1 ≤ -2P ≤ 1
⇒ 1 ≥ 2P ≥ -1
⇒ -1 ≤ 2P ≤ 1
⇒ \(\frac{-1}{2} \leq P \leq \frac{1}{2}\) ………(3)
From (1), (2), (3) we have \(\frac{-1}{3} \leq P \leq \frac{1}{2}\)
Question 11.
On a Festival day, a man plans to visit 4 holy temples A, B, C, D in random order. Find the probability that he visits (i) A before B (ii) A before B and B before C.
Solution:
(i) It is nothing but arranging A, B, C, D in 4 chains so that A seats before B.
For this, first, we arrange C, D is the 4 chains it can be done in 4P2 = 12 ways and the remaining 2 seats A & B can be sit in only one way (A before B).
Also n(S) = 24
∴ The probability that he visit 4 temples, A before B = \(\frac{12 \times 1}{24}\) = \(\frac{1}{2}\)
(ii) Similarly to the above problem
First, we arrange D in any one of 4 chains it can be done in 4 ways. Then the remaining 3 seats A, B, C can sit in only one way (A before 3 and B before C)
Also n(A) = 4! = 24
The probability that he visit 4 temples, A before B and B before C = \(\frac{4 \times 1}{24}\) = \(\frac{1}{6}\)
![]()
Question 12.
From the employees of a company, 5 persons are selected to represent them in the managing committee of the company. The particulars of 5 persons are as follows.
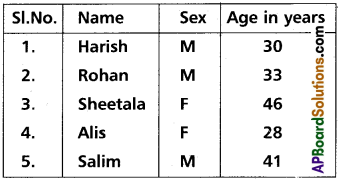
A person is selected at random from this group to act as a spokesperson. Find the probability that the spokesperson will be either male or above 35 years.
Solution:
Let A be the event that the selected person is male and B be the event that the selected person is above 35 years when a person is selected at random from the group of 5 persons to act as a spokesperson and S be the sample space.
∴ n(S) = 5C1 = 5
n(A) = 3C1 = 3
P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{3}{5}\)
n(B) = 2C1 = 2
P(B) = \(\frac{n(B)}{n(S)}\) = \(\frac{2}{5}\)
n(A ∩ B) = 1C1 = 1
P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}\) = \(\frac{1}{5}\)
By Addition theorem on probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{3}{5}+\frac{2}{5}-\frac{1}{5}\)
= \(\frac{4}{5}\)
Question 13.
Out of 100 students, two sections of 40 are 60 and formed. If you and your friend are among the 100 students, find the probability that
(i) You both enter the same section.
(ii) You both enter the different sections.
Solution:
Let S be the sample space
n(S) = no.of ways of doing 100 students into 2 sections of 40 and 60 = \(\frac{100 !}{40 ! 60 !}\)
(i) You both enter the same section:
First, you and your friend both enter the section the remaining 98 students and I can be divided into two sections (First section 38 and second section 60) is \(\frac{98 !}{38 ! 60 !}\)
You and your friend both enter section II and the remaining 98 students can be divided into two sections (First section 40 and second section 58) is \(\frac{98 !}{40 ! 58 !}\)

= \(\frac{26}{165}+\frac{59}{165}\)
= \(\frac{17}{33}\)
(ii) You both enter the different sections:
The probability that the both in different sections = 1 – P(E)
= 1 – \(\frac{17}{33}\)
= \(\frac{16}{33}\)