AP Board 6th Class Maths Solutions Chapter 10 Practical Geometry Ex 10.4

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 10 Practical Geometry Ex 10.4 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 10th Lesson Practical Geometry Ex 10.4

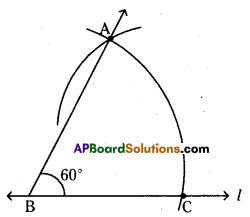
Question 1.
Construct ∠ABC = 60° without using protractor.
Solution:
Steps of construction :

1. Draw a line l and mark a point B on it.
2. Place the pointer of the compasses at B and draw an arc of convenient radius which cuts the line l at a point C.
3. With the pointer at C as centre and with the same radius as above. Now draw an arc that passes through B.
4. Cut intersecting point of two arcs is A. Join BA. ∠ABC = 60° is formed.
   Hence the required angle ∠ABC = 60° is constructed.
   

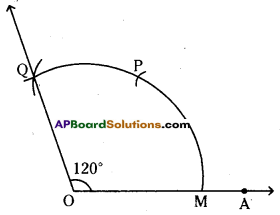
Question 2.
Construct an angle of 120° with using protractor and compasses.
Solution:
Steps of construction :

1. Draw a ray \(\overline{\mathrm{OA}}\) of any length.
2. Place the pointer of the compasses at O. With O as centre and any convenient radius draw an arc cutting OA at M.
3. With M as centre and without altering radius draw an arc which cuts the previous arc at P.
4. With P as centre and without changing radius draw an arc which cuts the first arc at Q.
5. Join OQ. Then ∠AOQ is the required angle.
   Hence the required angle ∠AOQ = 120° is constructed.
   

Question 3.
Construct the following angles using ruler and compasses. Write the steps of construction in each case.
i) 75°
ii) 15°
iii) 105°
Solution:
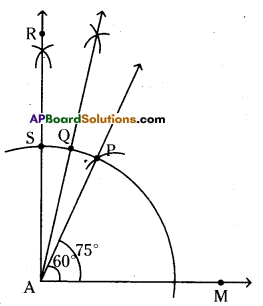
i) 75°
Steps of construction:

1. Construct ∠RAM 900
2. Construct ∠PAM = 600 AM as common arm
3. Now, ∠PAR = ∠RAM – ∠PAM = 90° – 60° = 30°
4. Draw bisector to ∠PAR which is \(\overrightarrow{\mathrm{AQ}}\).
5. Now, ∠MAQ = ∠PAM + ∠PAQ = 60° + \(\frac{30^{\circ}}{2}\)
   = 60° + 15° = 75° (QED)
   

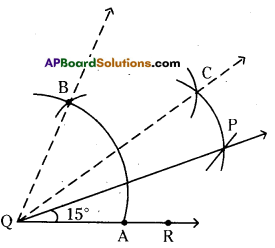
ii) 15°
Steps of construction:

1. Construct ∠BQR = 60°
2. Draw the bisector to ∠BQR which is \(\overrightarrow{\mathrm{QC}}\)
3. Now,∠CQR = \(\frac{60^{\circ}}{2}\) = 30°
4. Draw the bisector \(\overrightarrow{\mathrm{QP}}\) to∠CQR.
5. ∠PQR = \(\frac{1}{2}\) x 30° = 15° (Q.E.D)
   

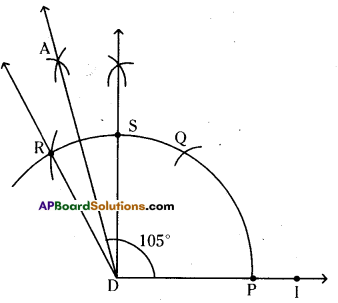
iii) 105°
Steps of construction :

1. Construct ∠IDS = 90°
2. Construct ∠ADS = \(\frac{\angle \mathrm{RDS}}{2}=\frac{30^{\circ}}{2}\) = 15°
3. Now, ∠ADI = ∠IDS + ∠ADS = 90° + 15°
   ∴ ∠ADI = 105° (Q.E.D)