AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 3 Polynomials Ex 3.4 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 3rd Lesson Polynomials Exercise 3.4
10th Class Maths 3rd Lesson Polynomials Ex 3.4 Textbook Questions and Answers
Question 1.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
i) p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2
ii) p(x) = x4 – 3×2 + 4x + 5, g(x) = x2 + 1 – x
iii) p(x) = x4 – 5x + 6, g(x) = 2 – x2
Answer:
i) Given polynomials are
p(x) = x3 – 3x2 + 5x – 3 and
g(x) = x2 – 2
Here, dividend and divisor are both in standard forms.
So, we have
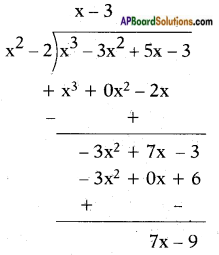
∴ The quotient is x – 3 and the remainder is 7x – 9.
![]()
ii) Given polynomials are
p{x) = x4 – 3x2 + 4x + 5 and
g(x) = x2 + 1 – x
Here, the dividend is already in the standard form and the divisor is not in the standard form. It can be written as x2 – x + 1.
We have,

∴ The quotient is x2 + x – 3 and the remainder is +8.
iii) Given polynomials are
p(x) = x4 – 5x + 6 and
g(x) = 2 – x2
Here, the dividend is already in the standard form and the divisor is not in the standard form. It can be written as -x2 + 2.
So, we have
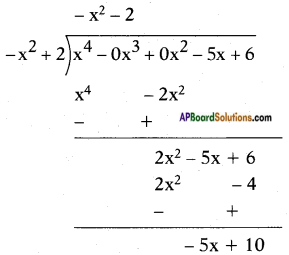
∴ The quotient is -x2 – 2 and the remainder is -5x + 10.
![]()
Question 2.
Check in which case the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
i) t2 – 3, 2t4 + 3t3 – 2t2 – 9t – 12
ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
iii) x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1
Answer:
i) Given first polynomial is t2 – 3.
Second polynomial is
2t4 + 3t3 – 2t2 – 9t – 12.
Let us divide 2t4 + 3t3 – 2t2 – 9t – 12 by t2 – 3, we get
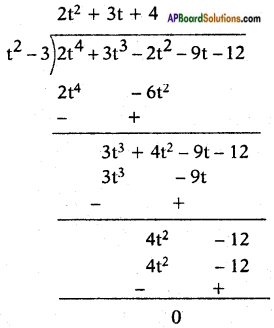
Since the remainder is 0, therefore, t2 – 3 is a factor of 2t4 + 3t3 – 2t2 – 9t – 12.
ii) Given first polynomial is x2 + 3x + 1
Second polynomial is 3x4 + 5x3 – 7x2 + 2x + 2
Let us divide 3x4 + 5x3 – 7x2 + 2x + 2 by x2 + 3x + 1, we get
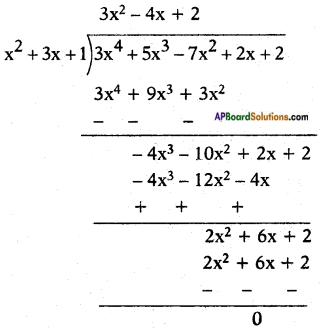
Since the remainder is 0, therefore x2 + 3x + 1 is a factor of 3x4 + 5x3 – 7x2 + 2x + 2.
![]()
iii) Given first polynomial = x3 – 3x + 1
Second polynomial = x5 – 4x3 + x2 + 3x + 1
Let us divide x5 – 4x3 + x2 + 3x + 1 by x3 – 3x + 1, we get

Here, remainder is 2(≠ 0).
Therefore, x3 – 3x + 1 is not a factor of x5 – 4x3 + x2 + 3x + 1.
Question 3.
Obtain all other zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeroes are \(\sqrt{\frac{5}{3}}\) and –\(\sqrt{\frac{5}{3}}\).
Answer:
Let the other two zeroes are α and β.
Now compare the given polynomial 3x4 + 6x3 – 2x2 – 10x – 5 with the standard form ax4 + bx3 + cx2 + dx + e we get a = 3, b = 6, c = -2, d = -10, e = -5

–\(\frac{5}{3}\)αβ = \(\frac{-5}{3}\) ⇒ αβ = 1
now (α – β)2 = (α + β)2 – 4αβ
= (-2)2 – 4(1)
= 4 – 4 = 0
α – β = 0 …. (2)
Now solving (1) and (2) we get

⇒ α = -1, β = -1
Then the remaining the zeroes are -1 and -1.
Hence all zeroes of it = –\(\sqrt{\frac{5}{3}}\), \(\sqrt{\frac{5}{3}}\), -1, -1.
![]()
Question 4.
On dividing x3 – 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and -2x + 4, respectively. Find g(x).
Answer:
Given, p(x) = x3 – 3x2 + x + 2
q(x) = x – 2 and
r(x) = -2x + 4
By division algorithm, we know that Dividend = Divisor × Quotient + Remainder
p(x) = q(x) × g(x) + r(x)
Therefore, x3 – 3x2 + x + 2
= (x – 2) × g(x) + (- 2x + 4)
⇒ x3 – 3x2 + x + 2 + 2x – 4 = (x – 2) × g(x)
g(x) = \(\frac{x^{3}-3 x^{2}+3 x-2}{x-2}\)
On dividing x3 – 3x2 + x + 2, by x – 2, we get

First term of g(x) = \(\frac{\mathrm{x}^{3}}{\mathrm{x}}\) = x2
Second term of g(x) = \(\frac{-x^{2}}{x}\) = -x
Third term of g(x) = \(\frac{x}{x}\) = 1
Hence, g(x) = x2 – x + 1.
Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
i) deg p(x) = deg q(x)
ii) deg q(x) = deg r(x)
iii) deg r(x) = 0
Answer:
Let q(x) = 3x2 + 2x + 6, degree of q(x) = 2
p(x) = 12x2 + 8x + 24, degree of p(x) = 2
Given degree p(x) = degree q(x)
i) Using division algorithm,
We gave, p(x) = q(x) × g(x) + r(x)
On dividing 12x2 + 8x + 24 by 3x2 + 2x + 6, we get

Since, the remainder is zero, therefore 3x2 + 2x + 6 is a factor of 12x2 + 8x + 24.
∴ g(x) = 4 and r(x)= 0
![]()
ii) Let p(x) = x5 + 2x4 + 3x3 + 5x2 + 2
q(x) = x2 + x + 1, degree q(x) = 2
Given degree q(x) = degree r(x)
On dividing x5 + 2x4 + 3x3 + 5x2 + 2 by x2 + x + 1, we get

Here, g(x) = x3 + x2 + x + 1 and r(x) = 2x2 – 2x + 1
degree of r(x) = 2.
∴ deg g(x) = deg r(x).
iii) Let p(x) = 2x4 + 8x3 + 6x2 + 4x + 12, r(x) = 2
Here, degree r(x) = 0
On dividing 2x4 + 8x3 + 6x2 + 4x + 12 by 2, we get
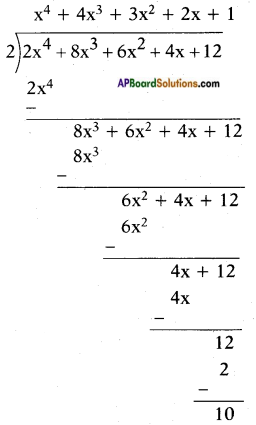
Here, g(x) = x4 + 4x3 + 3x2 + 2x + 1 and r(x) = 10
so degree of r(x) = 0
