AP State Syllabus AP Board 9th Class Maths Solutions Chapter 15 Proofs in Mathematics InText Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 15th Lesson Proofs in Mathematics InText Questions
![]()
Do This
Question
Make 5 more sentences and check whether they are statements or not ? * Give reasons. [Page No. 311]
Solution:
1) 9 is a prime number – False
This is a statement because we can judge the truthness of this sentence. Clearly it is a false statement as 9 has factors other than 1 and 9, hence it is a composite number.
2) x is less than 5 – can’t say True or False
This is not a statement. The truthness can t be verified unless the value of x is known. Hence it is a sentence only.
3) 3 + 5 = 8 – True
The above sentence is a statement. It is a true statement as 5 + 3 = 8.
4) Sum of two odd numbers is even – True
The above sentence can be verified as a true sentence by taking ex¬amples like 3 + 5 = 8, 5 + 7 = 12 etc. Hence it is a true statement.
5) \(\frac{\mathrm{X}}{2}\) +3 = 9- can’t say True or False.
The above sentence is not a state¬ment. Its truthness can’t be
verified without the value of x.
![]()
Try This
1. 3 is a prime number.
2. Product of two odd integers is even.
3. For any real number x; 4x T x = 5x
4. The earth has one moon.
5. Ramu is a good driver.
6. Bhaskara has written a book “Leelavathi ”.
7. All even numbers are composite.
8. A rhombus is a square.
9. x > 7.
10. 4 and 5 are relative primes.
11. Silver fish is made of silver.
12. Humans are meant to rule the earth.
13. For any real number .v. 2x > x.
14. Havana is the capital of Cuba.
Question
Which of the above statements can be tested by giving counter example ?
[Page No. 312]
Solution:
Statements 2, 7, 8, 13 can be tested by giving counter examples 2) Product of two odd integers is even. Counter example.
2) Product of two odd integers 3 and 5 is 3×5 = 15 is not an even number.
7) All even numbers are composite. Counter example : 2 is an even prime.
8) A rhombus is a square.

Counter example: (40°, 140°, 40°. 140°) is a rhombus.
13) For anyx; 2x > x
Counter example : for x = -3:
2x = 2(-3) = – 6
here -6 < – 3
![]() b
b
Try This
Envied by the popularity of Pythagoras, his younger brother claimed a different relation between the sides of a right angled triangles. [Page No. 319]
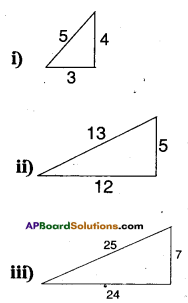
Liethagoras Theorem: In any right angled triangle the square of the smallest side equals the sum of the other sides. Check this conjecture, whether It is right or wrong.
Solution:
This conjecture is true for the above
triangles.
i) 32 5 + 4 ⇒ 9 = 5 + 4
ii) 52 = 25 = 12 + 13
iii) 72 = 49 = 24 + 25
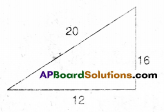
But, when the smallest side happens to be an even integer the conectiire may not hods good.
Eg: 1) 62 = 36 ≠ 10 + 8
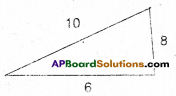
ii) 122 = 144 ≠ 20 + 16