AP SSC 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Optional Exercise

AP State Syllabus SSC 10th Class Maths Solutions 9th Lesson Tangents and Secants to a Circle Optional Exercise

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Questions and Answers.

10th Class Maths 9th Lesson Tangents and Secants to a Circle Optional Exercise Textbook Questions and Answers

Question 1.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line – segment joining the points of contact at the centre.
Answer:

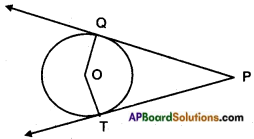
Given: A circle with centre ‘O’.
Two tangents \(\overleftrightarrow{\mathrm{PQ}}\) and \(\overleftrightarrow{\mathrm{PT}}\) from an external point P. Let Q, T be the points of contact.
R.T.P: ∠P and ∠QOT are supplementary.
Proof: OQ ⊥ PQ
[∵ radius is perpendicular to the tangent at the point of contact] also OT ⊥ PT
∴ ∠OQP + ∠OTP = 90° + 90° = 180° Nowin oPQOT,
∠OTP + ∠TPQ + ∠PQO + ∠QOT
= 360° (angle sum property)
180° + ∠P + ∠QOT = 360°
∠P + ∠QOT = 360°- 180° = 180° Hence proved. (Q.E.D.)

Question 2.
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (See figure). Find the length of TP.

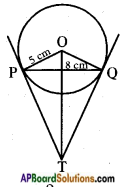
Answer:

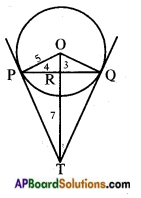
Given: PQ = 8
⇒ PR = 4
⇒ PO² = PR² + OR²
⇒ 25 = 16 + OR²
⇒ OR = 3
Now let RT = x and PT in △OPT, ∠P = 90°
∴ OT is hypotenuse.
∴ OT² = OP² + PT²
(Pythagoras theorem)
(3 + x)² = 5² + y² …….. (1)
and in △PRT, ∠R = 90°
∴ \(\overline{\mathrm{PT}}\) is hypotenuse.
∴ PT² = PR² + RT²
y² = 4² + x² …….. (2)
Now putting the value of y² = 4² + x² in equation (1) we got
(3 + x)² = 5² + x² + 4²
9 + x² + 6x = 25 + 16 + x²
6x = 25 + 16 – 9 = 25 + 7 = 32
⇒ x = \(\frac{32}{6}\) = \(\frac{16}{3}\)
Now from equation (2), we get

Question 3.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Answer:

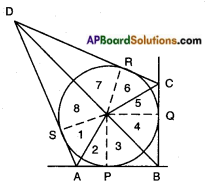
Given: Let a circle with centre ‘O’ touches the sides AB, BC, CD and DA of a quadrilateral ABCD at the points P, Q, R and S respectively.
R.T.P: ∠AOB + ∠COD = 180°
∠AOD + ∠BOC = 180°
Construction: Join OP, OQ, OR and OS.
Proof: Since the two tangents drawn from an external point of a circle subtend equal angles.
At the centre,
∴ ∠1 = ∠2
∠3 = ∠4 (from figure)
∠5 = ∠6
∠7 = ∠8
Now, ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
[∵ Sum of all the angles around a point is 360°]
So, 2 (∠2 + ∠3 + ∠6 + ∠7) = 360°
and 2 (∠1 + ∠8 + ∠4 + ∠5) = 360°
(∠2 + ∠3) + (∠6 + ∠7) = \(\frac{360}{2}\) = 180°
Also, (∠1 + ∠8) + (∠4 + ∠5) = \(\frac{360}{2}\) = 180°
So, ∠AOB + ∠COD = 180°
[∵ ∠2 + ∠3 = ∠AOB;
∠6 + ∠7 = ∠COD
∠1 + ∠8 = ∠AOD
and ∠4 + ∠5 = ∠BOC [from fig.]]
and ∠AOD + ∠BOC = 180°

Question 4.
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Answer:

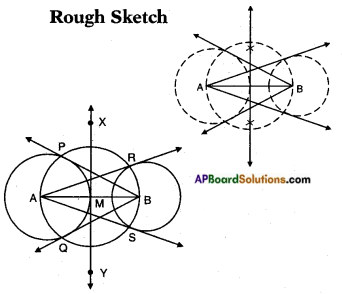
Steps of construction:

1. Draw a line segment AB of length 8 cm.
2. With A and B as centres and 4 cm, 3 cm as radius draw two circles.
3. Draw the perpendicular bisectors \(\stackrel{\leftrightarrow}{\mathrm{XY}}\) of AB. Let \(\stackrel{\leftrightarrow}{\mathrm{XY}}\) and AB meet at M.
4. Taking M as centre and MA or MB as radius draw a circle which cuts the circle with centre A at P and Q and circle with centre B at R, S.
5. Join BP, BQ and AR, AS.

Question 5.
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Answer:

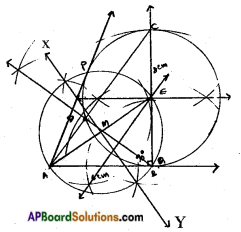
Steps of construction:

1. Draw AABC such that AB = 6 cm; ∠B = 90° and BC – 8 cm.
2. Drop a perpendicular BD from B on AC.
3. Draw the circumcircle to ABCD. Let ‘E’ be its centre.
4. Join AE and draw its perpendicular bisector \(\stackrel{\leftrightarrow}{\mathrm{XY}}\). Let it meet AE at M.
5. Taking M as centre and MA or ME as radius draw a circle, which’ cuts the circumcircle of △BCD at P and B.
6. Join AP and extend AB, which are the required tangents.

Question 6.
Find the area of the shaded region in the figure, given in which two circles with centres A and B touch each other at the point C. If AC = 8 cm. and AB = 3 cm.

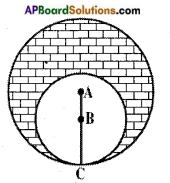
Answer:
Given: Two circles with centres A and B, whose radii are 8 cm and 5 cm.
[∵ AC = 8 cm, AB = 3 cm ⇒ BC = 8 – 3 = 5 cm]
Area of the shaded region = (Area of the larger circle) – (Area of the smaller circle)

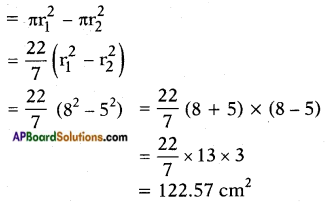
Question 7.
ABCD is a rectangle with AB = 14 cm. and BC = 7 cm. Taking DC, BC and AD as diameters, three semicircles are drawn as shown in the figure. Find the area of the shaded region.

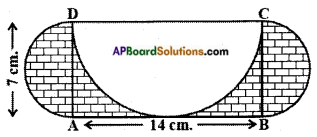
Answer:
Given AB = 14 cm, AD = BC = 7 cm Area of the shaded and unshaded region
= (2 × Area of the semi-circles with AD as diameter) + Area of the rectangle