AP State Syllabus AP Board 8th Class Maths Solutions Chapter 15 Playing with Numbers Ex 15.1 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 15th Lesson Playing with Numbers Exercise 15.1
![]()
Question 1.
Using divisibility rules, fmd which of the following numbers are divisible by 2,5,10 ( say
yes or no ) in the given table. What do you observe?

Solution:
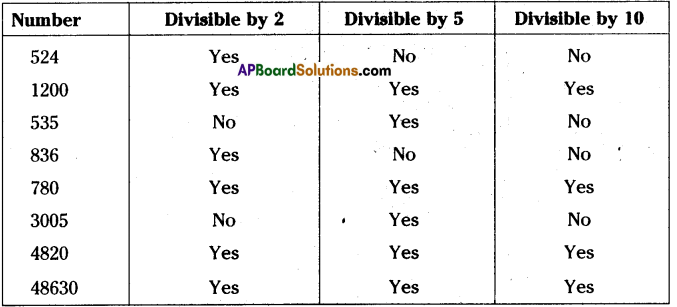
![]()
Question 2.
Using divisibility tests, determine which of following numbers are divisible by 2
(a) 2144 (b) 1258 (c) 4336 (d) 633 (e) 1352
Solution:
If a number is divisible by 2 then the units digit of the number be 0, 2, 4, 6, 8.
∴ a) 2144, b) 1258, c) 4336 e) 1352 are divisible by ‘2’.
Question 3.
Using divisibility tests, determine which of the following numbers are divisible by 5
(a) 438750 (b) 179015 (c) 125 (d) 639210 (e) 17852
Solution:
If a number is divisible by 5 its units digit be either ‘0’ or 5.
∴ a) 438750, b) 179015, c) 125 d) 639210 are divisible by 5.
Question 4.
Using divisibility tests, determine which of the following numbers are divisible by 10:
(a) 54450 (b) 10800 (c) 7138965 (d) 7016930 (e) 10101010
Solution:
If a number is divisible by 10 then its units digit must be 0’.
a) 54450, b) 10800, d) 7016930, e) 1010100 are divisible by 10.
![]()
Question 5.
Write the number of factors of the following’?
(a) 18 (b) 24 (e) 45 (d) 90 (e) 105
Solution:
| Number | Factors , | No.of factors |
| a) 18 | 1,2,3,6,9,18 | 6 |
| b) 24 | 1, 2, 3, 4, 6, 8, 12, 24 | 8 |
| c) 45 | 1,3,5,9,15,45 | 6 |
| d) 90 | 1, 2, 3, 5, 6, 9,10, 15, 18, 30, 45, 90 | 12 |
| e) 105 | 1,3, 5, 7,15,21,35,105 | 8 |
Question 6.
Write any 5 numbers which are divisible by 2,5 and 10.
Solution:
10, 20, 30, 40. are divisible by 2, 5 and 10
[∵ The L.C.M. of 2, 5, 10 is 10]
![]()
Question 7.
A number 34A is exactly divisible by 2 and leaves a remainder 1, when divided by 5, find A.
Solution:
If 34A Is divisible by 2 then the remainder should be equal to 0.
∴ A should be equal to 0, 2, 4, 6, 8.
∴ 340, 342, 344, 346, 348 are divisible by 2 and gives the remainder ‘0’.
Among these 346 is divisible by 5 and gives the remainder 1.
∴ 346 → \(\frac{6}{5}\) (R = 1)
∴ The value of A = 6.
