Practice the AP 10th Class Maths Bits with Answers Chapter 1 Real Numbers on a regular basis so that you can attempt exams with utmost confidence.
AP State Syllabus 10th Class Maths Bits 1st Lesson Real Numbers with Answers
Question 1.
Find the rational number in between \(\frac { 1 }{ 2 }\) and √1
Answer:
\(\frac { 3 }{ 4 }\)
Question 2.
Write the name set of rational and ir-rational numbers.
Answer:
Real numbers.
![]()
Question 3.
Write the logarithmic form of 35 = 243.
Answer:
log3243 = 5
Question 4.
Write the symbol of “implies”.
Answer:
⇒
Question 5.
Write the prime factorisation of 729.
Answer:
36
Question 6.
If ‘x’ and ‘y’ are two prime numbers, then find their HCF.
Answer:
1
Explanation:
HCF of any two prime numbers is always 1.
Question 7.
Find the value of log10 0.01.
Answer:
-2
Explanation:
log100.01 = log10 \(\frac{1}{10^{2}}\)
= log1010-2 = – 2
Question 8.
Find the number of odd numbers in between ‘0’ and 100.
Answer:
50
Question 9.
Write the exponential form of log48 = x.
Answer:
4x = 8.
Explanation:
Exponential form of log48 = x is 4x = 8
Question 10.
How much the value of \(\frac{36}{2^{3} \times 5^{3}}\) in decimal form ?
Answer:
0.036.
![]()
Question 11.
LCM of two numbers is 108 and their HCF is 9 and one of them is 54, then find the second one.
Answer:
18
Explanation:
LCM x HCF = one number x second number
108 x 9 = 54 x second one , 108 x 9
⇒ Second one = \(\frac{108 \times 9}{54}\) = 18.
Question 12.
\(\frac { 3 }{ 8 }\) is example for decimal.
Answer:
Terminating decimal.
Question 13.
If \(\mathbf{a} \sqrt{\mathbf{c}}=\sqrt{\mathbf{a c}}\) , then find the value of ‘a’, (a, c are positive integers),
Answer:
a = 1
Question 14.
Find the value of 9 – \(0 . \overline{9}\).
Answer:
8
Explanation:
9 – \(\frac{9}{9}\) = 9 – 1 = 8.
Question 15.
Write rational number that equals to \(2 . \overline{6}\)
Answer:
\(\frac { 8 }{ 3 }\)
Question 16.
Write the value of log25 5.
Answer:
\(\frac { 1 }{ 2 }\)
Explanation:
log255 = log551 = \(\frac{1}{2}\)log55 = \(\frac{1}{2}\)
Question 17.
The fundamental theorem of arithmetic is applicable to, which least number ?
Answer:
2
![]()
Question 18.
Find the last digit of 650.
Answer:
6
Question 19.
Which of the following is a terminat¬ing decimal ?
A) \(\frac { 10 }{ 81 }\)
B) \(\frac { 41 }{ 75 }\)
C) \(\frac { 8 }{ 125 }\)
D) \(\frac { 3 }{ 14 }\)
Answer:
C)
Question 20.
Find the value of log2 32.
Answer:
5
Question 21.
Which of the following is not irrational ?
A) √2
B) √3
C) √4
D) √5
Answer:
(C)
Question 22.
Find the value of log10 0.001.
Answer:
-3
Question 23.
Find the number of prime factors of 36.
Answer:
2 and 3
Explanation:
36 = 22 x 32
∴ Two prime numbers i.e., 2 and 3.
Question 24.
Write the exponential form of
Iog10 = -3.
Answer:
10-3 = 0.001
Question 25.
Define an irrational number.
Answer:
Which cannot be written in the form
of p/q where p, q ∈ Z, q ≠ 0.
Question 26.
Find the LCM of 24 and 36.
Answer:
72
![]()
Question 27.
Find the logarithmic form of ab = c.
Answer:
logac = b.
Question 28.
If 3 log (x + 3) = log 27, then find the value of x.
Answer:
0
Explanation:
3 log (x + 3) = log 27
⇒ log (x + 3)3 = log 33
⇒ x + 3 = 3 ⇒ x = 0
log3729 = x ⇒ 3x = 729 = 36 ⇒ x = 6
Question 29.
If P1 and P2 are two odd prime num-bers, such that P1 > P2, then the value of \(\mathbf{P}_{1}^{2}-\mathbf{P}_{\mathbf{2}}^{2}\) results number
Answer:
An even number.
Question 30.
Find the value of \(\log _{10} 2+\log _{10} 5\)
Answer:
1
Question 31.
If log3 729 = x, then find the value of x.
Answer:
6
Explanation:
log3 729 = x ⇒ 3x = 729 = 36 ⇒ x = 6
Question 32.
Write the number of digits in the fractional part of the decimal form of \(\frac{7}{40}\).
Answer:
3
Explanation:
\(\frac{7}{40}=\frac{7}{2^{3} \times 5^{1}}\)
In Denominator 2n x 5m is equal to 3.
Question 33.
Write the prime factorization of 144.
Answer:
24 x 32
Question 34.
Find the number of prime factors of 72.
Answer:
2
Question 35.
log3 x2 = 2, then find the value of x.
Answer:
3
Explanation:
log3x2 = 2 ⇒ 32 = x2 ⇒ x = 3
Question 36.
Find the value of \(9 \sqrt{2} \times \sqrt{2}\)
Answer:
18
Question 37.
Find the value of log0.1 0.01.
Answer:
2
Explanation:
log 0.1 0.01 = log10-1 10-2
= \(\frac{-2}{-1}\) log10 10 = 2
Question 38.
0.3030030003 ………………. is an ………………. number.
Answer:
Irrational.
![]()
Question 39.
\(\frac{27}{82}\) is a …………. decimal.
Answer:
Non-terminating
Question 40.
If log 2 = 0.30103, then find log 32.
Answer:
1.50515
Explanation:
log 32 = log 25 = 5 log 2
= 5 x 0.30103 .
= 1.50515
Question 41.
Expand log 15.
Answer:
log5 + log3
Question 42.
Find the value of log10 10.
Answer:
1
Question 43.
Calculate the value of log8 128.
Answer:
\(\frac{7}{3}\)
Question 44.
Find the value of \(5 \sqrt{5}+6 \sqrt{5}-2 \sqrt{5}[/latex[
Answer:
9√5
Question 45.
743.2111111 … is a number.
Answer:
Rational
Question 46.
Find the value of log5 125.
Answer:
3
Question 47.
Expand log10 [latex]\frac{125}{16}\)
Answer:
3 log 5 – 4 log 2
Explanation:
log10 \(\frac{125}{16}\) = log10 125 – log1016
= log1053 – log1024
= 3 log 5 – 4 log 2
Question 48.
Find the L.C.M of the numbers 27 x 34 x 7 and 23 x 34 x 11.
Answer:
27 x 34 x 7 x 11
Question 49.
If loga ax2 – 5x + 8 = 2, then find x.
Answer:
2 or 3.
Explanation:
\(\log _{a} a^{x^{2}-5 x+8}=\log _{a} a^{2}\)
{2 was write down as 2-loga a}
x2 – 5x + 8 = 2
x2 – 5x + 6 = 0
by solving equation x = 2 or 3
Question 50.
Find the value of loga \(\frac{1}{a}\).
Answer:
– 1
Question 51.
Find the value of log1 1.
Answer:
Not defined.
Question 52.
If log10 0.00001 = x, then find x.
Answer:
-5
![]()
Question 53.
Find the value of logb a • loga b.
Answer:
1.
Question 54.
16 x 64 = 4k, then find the value of k.
Answer:
5
Explanation:
16 x 64 = 4k
⇒ 42 x 43 = 4k
⇒ 45 = 4k
⇒ k = 5
I’m
Question 55.
Write exponential form of log464 = 3.
Answer:
43 = 64
Question 56.
Calculate the value of \(\log _{9} \sqrt{3 \sqrt{3 \sqrt{3}}}\)
Answer:
\(\frac{7}{16}\)
Question 57.
If ‘m’ and ‘n’ are co-primes, then find H.C.F of m2 and n2.
Answer:
1
Question 58.
\(\sqrt{5}+\sqrt{7}\) is number.
Answer:
An irrational.
Question 59.
Find the H.C.F. of the numbers
37 x 53 x 24 and 32 x 74 x 28.
Answer:
24 x 32
Question 60.
\(\frac{13}{125}\) is a ……………… decimaL
Answer:
Terminating
Question 61.
Write the decimal expansion of 0.225 in its rational form.
Answer:
\(\frac{9}{40}\)
Question 62.
How many prime factors are there in the prime factorization of 240.
Answer:
3
Question 63.
14.381 may certain the denominator when expressed in p/q form.
Answer:
23 x 53
Question 64.
By which numbers 7 x 11 x 17 +34 is divisible, write them.
Answer:
17 and 79
Explanation:
Given number = 7 x 11 x 17 + 34
= 17 (7 x 11 + 2)
= 17 x 79
Given number has 17 and 79 are factors.
Question 65.
Write log\(\frac{x^{2} y^{3} z^{4}}{w^{5}}\) in the expanded form.
Answer:
2 log x + 3 log y + 4 log z – 5 log w
Explanation:
log x2y3z4 – log w5 = log x2 + log y3 + log z4 – log w5
= 2log x + 3log y + 4log z – 51og w
Question 66.
Write the logarithmic form of 122 = 144.
Answer:
log12 144 = 2
Question 67.
Expand log 81 x 25.
Answer:
4log 3 + 2 log 5
Question 68.
What is the L.C.M. of greatest two digit number and the greatest three digit number.
Answer:
9 x 11 x 111
Question 69.
Write logarithmic form of 192 = 361.
Answer:
log19361 = 2
Question 70.
3 X 5 x 7 x 11 + 35 is number.
Answer:
Composite
Question 71.
Write the decimal expansion of \(\frac{101}{99}\).
Answer:
\(1 . \overline{02}\)
Question 72.
If P1, p2, p3, …………… pn are co-primes, then
their LCM is
Answer:
P1p2 …………… pn
Question 73.
In the above problem find HCF.
Answer:
1
Question 74.
n2 – 1 is divisible by 8, if ‘n’ is number.
Answer:
An odd number.
![]()
Question 75.
If x and y are any two co-primes, then find their L.C.M.
Answer:
x.y
Question 76.
Write \(\frac{70}{71}\) is which type of decimal ?
Answer:
Non-terminating, repeating.
Question 77.
0.12 112 1112 11112………………is…………… type of number.
Answer:
Irrational
Question 78.
Write \(\frac{123}{125}\) is which type of decimal ?
Answer:
Terminating.
Question 79.
Write the product of L.C.M. and H.C.F. of the least prime and least composite number.
Answer:
8
Question 80.
\(\sqrt{2}-2\) is…………………number.
An irrational.
Question 81.
Find the number of prime factors of 1024.
Answer:
Only one number, i.e., ‘2’. (i.e., 210)
Question 82.
Write the LCM of 208 and 209.
Answer:
208 x 209 (Product of even and odd number is its product)
Question 83.
Write the expansion of \(\frac{87}{625}\) terminates after how many places ?
Answer:
4 places.
Question 84.
The decimal expansion of \(\frac{87}{625}\) terminates after how many places ?
Answer:
4 places.
Question 85.
What is the H.C.F. of ‘n’ and ‘n + 1’, where ‘n’ is a natural number ?
Answer:
1
Question 86.
What is the prime factorisation of 20677.
Answer:
23 x 29 x 31
Question 87.
Find the HCF of 1001 and 1002.
Answer:
1
Question 88.
p, q are co-primes and q = 2n . 5m, where m > n, then write the decimal expansion of p/q terminates after how many places ?
Answer:
‘m’ places.
Question 89.
Write the decimal fprm of \(\frac{80}{81}\) and write repeats after how many places ?
Answer:
81 = 34, so not possible.
Question 90.
If a rational number p/q has a termi¬nating decimal, then write the prime factorisation of ‘q’ is of the form.
Answer:
q = 2m . 5n
Question 91.
Write the decimal expansion of \(\frac{7}{16}\) without actual division.
Answer:
0.4375
Question 92.
In the expansion of \(\frac{123}{125}\) terminates after how many places ?
Answer:
3 places.
Question 93.
What is the L.C.M of least prime and the least composite number ?
Answer:
Least composite
Question 94.
Write the decimal expansion of \(\frac{27}{14}\)
Answer:
\(1.9 \overline{285714}\)
![]()
Question 95.
Which type of number was \(5.6789 \overline{1}\) ?
Answer:
Rational number
Question 96.
After how many places the decimal expansion of \(\frac{23}{125}\) terminates ?
Answer:
3 places.
Question 97.
Write the type of decimal expansion of \(\frac{9}{17}\)
Answer:
Non-terminating & repeating.
Question 98.
Write the period of the decimal expansion of \(\frac{19}{21}\)
Answer:
904761
Question 99.
After how many digits will the deci-mal expansion of \(\frac{11}{32}\) terminates ?
Write it.
Answer:
5 places.
Question 100.
If \(\sqrt{2}\) = 1.414, then find \(3 \sqrt{2}\).
Answer:
4.242
Question 101.
Find the value of \(\frac{3}{8}\)
Answer:
0.375
Question 102.
Find the value of log 64 – log 4.
Answer:
16
Question 103.
Find the value of 128 ÷ 32.
Answer:
4
Question 104.
Find the value of 104.
Answer:
10000
Question 105.
Find the value of \(\sqrt{\mathbf{5}}\) .
Answer:
2.236
Question 106.
Find the value of log27 9.
Answer:
\(\frac{2}{3}\)
Question 107.
Find the value of | – 203 |.
Answer:
203
Question 108.
Complete the rule a(b + c).
Answer:
ab + ac
Question 109.
Find the value of log3 \(\frac{1}{9}\).
Answer:
-2
Question 110.
How much the LCM of 12, 15 and 21.
Answer:
420
Question 111.
Find the value of loga 1, a > 0.
Answer:
0
Question 112.
a + (-a) = 0 = (- a) + a is called ……………… property.
Answer:
Inverse
![]()
Question 113.
Find the value of \(\sqrt{\mathbf{a}} \times \sqrt{\mathbf{b}}\)
Answer:
\(\sqrt{a b}\)
Question 114.
Find the value of 55.
Answer:
3125
Question 115.
Find the value of \(\frac{13}{4}\) .
Answer:
3.25
Question 116.
Find the value of \(\sqrt{12544}\)
Answer:
112
Question 117.
Find the value of log61.
Answer:
0
Question 118.
Find the value of log1010000.
Answer:
4
Question 119.
How much the HCF of 12 and 18.
Answer:
6
Question 120.
Which number has no multiplicative inverse ?
Answer:
0
Question 121.
How much the LCM of 306 and 657.
Answer:
22338
Question 122.
Find the value of logx \(\frac{\mathbf{a}}{\mathbf{b}}\).
Answer:
logxa – logxb
Question 123.
Find the value of log32 \(\frac{1}{4}\)
Question 124.
Find the value of \(\sqrt{2025}\)
Answer:
\(\frac{-2}{5}\)
Question 125.
Find the value of \(2 \sqrt{3}+7 \sqrt{3}+\sqrt{3}\)
Answer:
\(10 \sqrt{3}\)
Question 126.
Find the value of 22 x 5 x 7.
Answer:
140
![]()
Question 127.
Find the value of log10 100.
Answer:
2
Question 128.
6n cannot end with this number. What is that number ? (When ‘n’ is a posi¬tive number).
Answer:
0
Question 129.
If 2x = y and log2 y = 3 then find (x – y)2.
Answer:
25
Question 130.
Find the value of log3 \(\frac{1}{27}\).
Answer:
-3
Question 131.
Expanded form of log101000.
Answer:
3 log 2 + 3 log 5
Question 132.
Find the value of log2512.
Answer:
9
Question 133.
Write \(\frac{3}{2}\) (log x) – (log y) as single form.
Answer:
\(\log \sqrt{\frac{x^{3}}{y^{2}}}\)
Question 134.
Find HCF of 1 and 143.
Answer:
1
Question 135.
Which of the following is a correct one ?
A) N⊂Z⊂W
B) N⊂W⊂Z
C) R⊂N⊂W
D) All the above
Answer:
(B)
Question 136.
Find the value of log216.
Answer:
4
Question 137.
Find the value of \(\log _{7} \sqrt{49}\)
Answer:
1
Question 138.
Find the value of log21024.
Answer:
10
Question 139.
Find the value of log18324.
Answer:
2
Question 140.
Express logarithmic form of ax = b.
Answer:
logab = x .
![]()
Question 141.
Find the value of \((\sqrt{7}+\sqrt{5}) \cdot(\sqrt{7}-\sqrt{5})\)
Answer:
2
Choose the correct answer satisfying the following statements.
Question 142.
Statement (A) : 6n ends with the digit zero, where ‘n’ is natural number. Statement (B): Any number ends with digit zero, if its prime factor is of the form 2m x 5n, where m, n are natural numbers.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Explanation:
6n = (2 x 3)n = 2n x 3n
Its prime factors do not contain 5n i.e., of the form 2m x 5n, where m, n are natural numbers. Here (A) is incorrect but (B) is correct.
Hence, (iii) is the correct option.
Question 143.
Statement (A) : \(\sqrt{a}\) is an irrational number, where ‘a’ is a prime number.
Statement (B) : Square root of any prime number is an irrational number.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
As we know that square root of every prime number is an irrational number. So, both A and B are correct and B explains A. Hence (i) is the correct option.
Question 144.
Statement (A) : For any two positive integers a and b,
HCF (a, b) x LCM (a, b) – a x b.
Statement (B) : The HCF of two num-bers is 5 and their product is 150. Then their LCM is 40.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)
Explanation:
We have,
LCM (a, b) x HCF (a, b) = a xb LCM x 5 – 150 150
∴ LCM = \(\frac{150}{5}\) = 30
=> LCM = 30, i.e., (B) is incorrect and (A) is correct.
Hence, (ii) is the correct option.
Question 145.
Statement (A) : When a positive inte-ger ’a’ is divided by 3, the values of re-mainder can be 0, 1 (or) 2.
Statement (B) : According to Euclid’s Division Lemma a = bq + r, where 0 ≤ r < b and ‘r’ is an integer.
i) Both A and B are true.
ii) A is true, 3 is false
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
Given positive integers A and B, there exists unique integers q and r satisfy¬ing a = bq + r where 0 ≤ r < b.
This is known as Euclid’s Division Algorithm. So, both A and B are cor¬rect and B explains A.
Hence, (i) is the correct option.
Question 146.
Statement (A): A number N when di¬vided by 15 gives the remainder 2. Then the remainder is same when N is divided by 5.
Statement (B) : \(\sqrt{3}\) is an irrational number.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)
![]()
Question 147.
Statement (A): \(\frac{41}{1250}\) is a terminating decimal.
Statement (B) : The rational number p/q is a terminating decimal if q = 2m x 5n, where m, n are non-nega¬tive integers.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Question 148.
Statement (A) : \(\sqrt{3}\) is an irrational number.
Statement (B) : The square root of a prime number is an irrational.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
Clearly, both A and B are correct but B does not explain A.
Hence, (i) is correct option.
Question 149.
Statement (A) : \(\frac{27}{250}\) is a terminating decimal.
Statement (B) : The rational number p/q is a terminating decimal, if q = (2m x 5n) for some whole number m and n.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Question 150.
Statement (A): \(\frac{13}{3125}\) is a terminating decimal fraction.
Statement (B): If q = 2n . 5m where n, m are non-negative integers, then p/q is terminating decimal fraction.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
(B) is correct.
Since the factors of the denominator 3125 is of the form 2° x 55.
∴ \(\frac{13}{3125}\) is a terminatmg decimal.
∴ Since (A) follows from (B).
∴ Hence, (i) is the correct option.
Question 151.
Statement (A) : Denominator of 34.12345 is of the form 2m x 5n, where m, n are non-negative integers.
Statement (B) : 34.12345 is a termi-nating decimal fraction.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
(B) is clearly true.
Again 34.12345 = \(\frac{3412345}{100000}\)
= \(\frac{682469}{20000}=\frac{682469}{2^{5} \times 5^{4}}\)
Its denominator is of the form 2m x 5n
[m = 5, n = 4 are non-negative integers.]
∴ (A) is true.
Since (B) gives (A).
Hence, (i) is the correct option.
Question 152.
Statement (A): The H.C.F. of two num-bers is 16 and their product is 3072. Then their L.C.M. = 162.
Statement (B): If a, b are two positive integers, then H.C.F x L.C.M = a x b.
i) Both A and B are true.
ii) A is true, B is false.-
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Explanation:
Here (B) is true (standard result)
(A) is false.
∴ \(\frac{3072}{16}\) = 192 ≠ 162
Hence, (iii) is the correct option.
![]()
Question 153.
Statement (A) : 2 is a rational num¬ber.
Statement (B): The square roots of all positive integers are irrationals.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)
Explanation:
Here (B) is not true.
∴ \(\sqrt{4} \neq 2\) which is not an irrational
number.
Clearly, (A) is true.
∴ (ii) is the correct option.
Question 154.
Statement (A) : If L.C.M. {p, q} = 30 and H.C.F. {p, q} = 5, then pq = 150.
Statement (B): L.C.M. of a, b x H.C.F. of a, b = a • b.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Question 155.
Statement (A) : n2 – n is divisible by 2 for every positive integer.
Statement (B): \(\sqrt{2}\) is a rational num¬ber.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)
Question 156.
Statement (A): n2 + n is divisible by 2 for every positive integer n.
Statement (B): If x and y are odd posi-tive integers, from x2 + y2 is divisible by 4.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Read the below passages and answer to the following questions.
If p is prime, then \(\sqrt{\mathbf{p}}\) is irrational and if a, b are two odd prime num-bers, then a2 – b2 is composite.
Question 157.
Is \(\sqrt{7}\) is a rational number ?
Answer:
No, it is an irrational number.
Question 158.
The results of 1192 – 1112 is a ………..
number.
Answer:
Composite
L.C.M. of several fractions
= \(\frac{\text { LCM of their numerators }}{\text { HCF of their denominators }}\)
H.C.F. of several fractions = \(\frac{\text { HCF of their numerators }}{\text { LCM of their denominators }}\)
![]()
Question 159.
Find the LCM of the fractions \(\frac{5}{16}, \frac{15}{24}\) and \(\frac{25}{8}\)
Answer:
\(\frac{75}{8}\).
Explanation:
L.C.M. of \(\frac{5}{16}, \frac{15}{24}\) and \(\frac{25}{8}\)
= \(\frac{\text { L.C.M. of numerators }}{\text { H.C.F. of denominators }}\)
L.C.M’. of 5, 15 and 25 is 75.
H.C.F. of 16, 24 and 8 is 8.
The H.C.F. of the given fractions = \(\frac{75}{8}\)
Question 160.
Find the HCF of \(\frac{2}{5}, \frac{6}{25}\) and \(\frac{8}{35}\).
Answer:
\(\frac{2}{175}\)
Explanation:
Question 161.
Find the HCF of the fractions \(\frac{8}{21}, \frac{12}{35}\) and \(\frac{32}{7}\)
Answer:
\(\frac{4}{105}\)
[H+] ion concentration in a soap used by Sohan is 9.2 x 10-22.
Explanation:
H.C.F. of given fraction is
\(\frac{\text { H.C.F. of } 8,12,32}{\text { L.C.M. of } 21,35,7}\)
= \(\frac{4}{105}\)
Question 162.
Which mathematical concept is used to find pH of a soap ?
Answer:
Logarithms.
Question 163.
How much the pH of soap used by Sohan ?
Answer:
pH = 21.04.
Question 164.
Write the correct matching options :
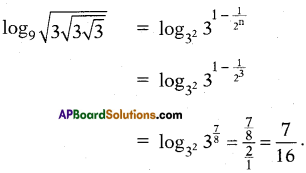
Answer:
A – (iii), B – (iv)
Question 165.
Write the correct matching options :

Answer:
A – (i), B – (ii)
Question 166.
Write the correct matching options :
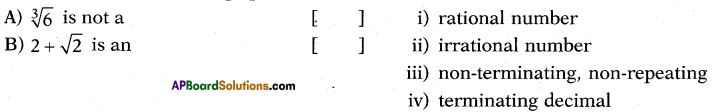
Answer:
A – (iii), B – (i)
Question 167.
Write the correct matching options :

Answer:
A – (ii), B – (v), C – (iii)
Question 168.
Write the correct matching options:

A – (i), B – (iv)
Question 169.
Write the correct matching options :

Answer:
A – (ii), B – (iii)
Question 170.
Write the correct matching options :

Answer:
A – (ii), B – (v)
Question 171.
Write the correct matching options:

Answer:
A – (iii), B – (iv)
Question 172.
Write the correct matching options:
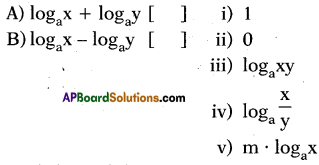
Answer:
A — (i), B – (ii), C — (v)
Question 173.
What is the value of \(\log _{\frac{2}{3}}\left(\frac{27}{8}\right)\)
Answer:
-3
Question 174.
Write the decimal form of the rational number \(\frac{7}{2^{2} \times 5}\)
AP Model Paper
Answer:
0.35
![]()
Question 175.
What is the value of \(\log _{\sqrt[3]{5}} \sqrt{5}\) ?
Solution:

Question 176.
Which statement do you agree with ? P: The product of two irrational num-bers is always a rational number.
Q : The product of a rational and an irrational number is always an irra-tional number,
i) Only P ii) Only Q iii) Both P and Q
Answer:
(ii)
Question 177.
Express 3 log22 = x in exponential form.
Solution:
3 log22 = x
log223 = x ⇒ log28 = x ⇒ 2x = 8