Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Hyperbola Solutions Exercise 5(a) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2B Hyperbola Solutions Exercise 5(a)
I.
Question 1.
One focus of a hyperbola is located at the point (1, -3) and the corresponding directrix is the line y = 2. Find the equation of the hyperbola if its eccentricity is \(\frac{3}{2}\).
Solution:
S(1 – 3) is thefocus, equation of the directrix is y – 2 = 0
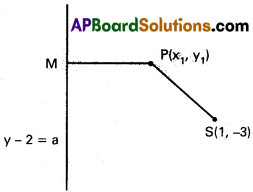
P(x1, y1) is any point on the hyperbola join SP and draw PM perpendicular to the directrix S.P = e. PM ⇒ SP² = e². PM²
(x1 – 1)² + (y1 + 3)² = \(\frac{9}{4}\)|\(\frac{(y_1-2}{\sqrt{1+0}}\)|²
x²1 + 1 – 2x1 + y²1 + 9 + 6y1 = \(\frac{9}{4}\) (y1 – 2)²
4x²1 + 4y²1 – 8x1 + 24y1 + 40 = 9(y²1 + 4 – 4y1) = 9y²1 – 36y1 + 36
4x²1 – 5y²1 – 8x1 + 60y1 + 4 = 0
Focus of P(x², y²) is
4x² – 5y² – 8x + 60y + 4 = 0
This is the equation of the required hyperbola.
Question 2.
If the lines 3x – 4y = 12 and 3x + 4y = 12 meets on a hyperbola S = 0 then find the eccentricity of the hyperbola S = 0.
Solution:
The given lines as
3x – 4y = 12
3x + 4y = 12
The combined equation of the lines
(3x – 4y) (3x + 4y) = 144
9x² – 16y² = 144

Question 3.
Find the equations of the hyperbola whose foci are (±5, 0) the transverse axis is of length 8.
Solution:
Foci are S(±5, 0) ∴ ae = 5
Length of transverse axis = 2a = 8
a = 4
e = \(\frac{5}{4}\)
b² = a² (e² – 1) = 16(\(\frac{25}{16}\) – 1)
Equation of the hyperbola is \(\frac{x^2}{16}-\frac{y^2}{9}\) = 1
9x² – 16y² = 144
![]()
Question 4.
Find the equation of the hyperbola, whose asymptotes are the straight lines (x + 2y + 3) = 0, (3x + 4y + 5) = 0 and which passes through the point (1, -1).
Solution:
Combined equation of the asymptotes as
(x + 2y + 3) (3x + 4y + 5) = 0
∴ Equation of the hyperbola can be taken as
(x + 2y + 3) (3x + 4y + 5) + k = 0
The hyperbola passes through P(1, -1)
(1 – 2 + 3) (3-4 + 5) + k = 0
8 + k = 0 ⇒ k = -8
Equation of the hyperbola is
(x + 2y + 3) (3x + 4y + 5) – 8 = 0
3x² + 6xy + 9x + 4xy + 8y² + 12y + 5x +10y + 15 – 8 = 0
3x² + 10xy + 8y² + 14x + 22y + 7 = 0
Question 5.
If 3x – 4y + k = 0 is a tangent to x² – 4y² = 5, find value of k.
Solution:
Equation of the hyperbola x² – 4y² = 5
\(\frac{x^2}{5}-\frac{y^2}{\left(\frac{5}{{4}}\right)}\) = 1
a² = 5, b² = \(\frac{5}{4}\)
Equation of the given line is 3x – 4y + k = 0
4y = 3x + k
y = \(\frac{3}{4}\)x + \(\frac{k}{4}\)
m = \(\frac{3}{4}\) c = \(\frac{k}{4}\)
Condition for tangency is c² = a²m² – b²
\(\frac{k^2}{16}\) = 5. \(\frac{9}{16}-\frac{5}{4}\)
k² = 45 – 20 = 25
k = ±5.
Question 6.
Find the product of lengths of the perpen-diculars from any point on the hyperbola \(\frac{x^2}{16}-\frac{y^2}{9}\) = 1 to its asymptotes.
Solution:
Equation of the hyperbola is \(\frac{x^2}{16}-\frac{y^2}{9}\) = 1
a² = 16, b² = 9
Product of the perpendiculars from any point as the hyperbola to its asymptotes
![]()
Question 7.
If the eccentricity of a hyperbola is \(\frac{5}{4}\), then find the eccentricity of its conjugate-hyperbola.
Solution:
If e and er, are the eccentricity of a hyperbola and its conjugate hyperbola, then

Question 8.
Find the equation of the hyperbola whose asymptotes are 3x = ± 5y and the vertices are (± 5, 0).
Solution:
The equation of the asymptotes are
3x = ±5y
3x – 5y = 0, 3x + 5y = 0
Combined equation of the asymptotes is
(3x – 5y) (3x + 5y) = 0
9x² – 25y² = 0
Equation of the hyperbola is 9x² – 25y² = k
The hyperbola passes through the vertex (5, 0)
9(5)² – 0 = k ⇒ k = 225
Equation of the hyperbola is
9x² – 25y² = 225
![]()
Question 9.
Find the equation of the normal at θ = \(\frac{\pi}{3}\) to the hyperbola 3x² – 4y² = 12.
Solution:
Equation of the hyperbola is 3x² – 4y² = 12
\(\frac{x^2}{4}+\frac{y^2}{3}\) = 1
Equation of the normal is
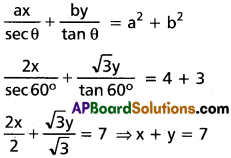
Question 10.
If the angle between the asymptotes is 30° then find its eccentricity.
Solution:
Angle between the asymptotes = 2θ = 30°
θ = 15°
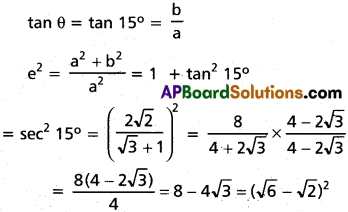
Eccentricity = e = √6 – √2
II.
Question 1.
Find the centre, foci, eccentricity equation of the directrices, length of the latus rectum of the following hyperbola.
i) 16y² – 9x² = 144
Solution:
Equation of the hyperbola is
16y² – 9x² = 144
\(\frac{y^2}{9}-\frac{x^2}{16}\) = 1
a² = 16, b² = 9
Centre C(0, 0)
b²e² = a² + b² = 16 + 9
= 25 ⇒ be = 5
Foci are 5(0, ±ae) = (0, ±5)
Eccentricity = \(\frac{be}{b}=\frac{5}{3}\)
Equation of the directrices are y = ±b/e
± 3. \(\frac{5}{3}\)
5y = ± 9
Length of the latus return = 2. \(\frac{a^2}{b}\)
= 2. \(\frac{16}{3}\) = \(\frac{32}{3}\)
ii) x² – 4y² = 4
Solution:
Equation of the hyperbola is \(\frac{x^2}{4}-\frac{y^2}{1}\) = 1
a² = 4, b² = 1
Centre is c (0,0)
a²e² = a² + b² = 4 + 1 = 5
ae = √5
Foci are (±ae, 0) = (± √5, 0)
Eccentricity = \(\frac{ae}{a}=\frac{\sqrt{5}}{2}\)
Equations of directrices are x = ±\(\frac{a}{e}\)
= ± 2. \(\frac{2}{\sqrt{5}}\)
⇒ √5 = ± 4
⇒ √5x ± 4 = 0
Length of the latus rectum = \(\frac{2b^2}{a}=\frac{2.1}{2}\) = 1
iii) 5x² – 4y² + 20x + 8y = 4
Solution:
5(x² + 4x + 4) -4 (y² – 2y + 1) = 4 + 20 – 4
5(x + 2)² – 4(y – 1)² = 20
\(\frac{(x+2)^2}{4}+\frac{(y-1)^2}{5}\) = 1
a² = 4, b² = 5 => a < b
Centre C(-2, +1)
a²e² = a² + b² = 4 + 5 = 9
ae = 3
Eccentricity = \(\frac{ae}{a}=\frac{3}{2}\)
Foci are (h ± ae, k) = (-2 ± 3, 1)
= (-5, 1) and (1, 1)
Equations of the directrices are x – h = ±\(\frac{a}{e}\)
x + 2 = ± 2. \(\frac{2}{3}\)
3x + 6 = ± 4
3x+ 10 = 0 or 3x + 2 = 0
Length of the latus rectum = \(\frac{2b^2}{a}=\frac{2.5}{2}\) = 5
iv) 9x² – 16y² + 72x – 32y – 16 = 0
Solution:
Equation of the hyperbola is
9x² – 16y² + 72x – 32y -16 = 0
⇒ 9(x² +8x) – 16(y² + 2y) = 16
⇒ 9(x² + 8x +16) – 16 (y² + 2y + 1)
= 16 + 144 – 16
⇒ 9(x + 4)² – 16(y + 1)² = 144
\(\frac{(x+4)^2}{16}+\frac{(y+1)^2}{9}\) = 1
Comparing with \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}\) = 1
a² = 16, b² = 9, h = -4, k = -1
Centre (h, k) = (-4, -1)

Foci = (h ± ae, k) = (- 4±4.\(\frac{5}{4}\), 1)
= (-4 ± 5, -1)
= (1, -1) and (-9, -1)
Equation of the directrices are
x + 4 = ± 4. \(\frac{4}{5}\)
= ± \(\frac{16}{5}\)
5x + 20 = ± 16
Equation of the directices are 5x + 4 = 0
and 5x + 36 = 0
Length of Latus rectum = \(2\frac{b^2}{a}=\frac{2.9}{4}=\frac{9}{2}\)
![]()
Question 2.
Find the equation to the hyperbola whose foci are (4, 2) and (8, 2) and eccentricity is 2.
Solution:
Foci are (4, 2) and (8, 2) Centre C is the mid point of the foci
∴ Centre is (\(\frac{4+8}{2}\), \(\frac{2+2}{2}\)) = (6, 2)
ae = 6 – 4 = 2
Given e = 2 ⇒ a = \(\frac{ae}{e}=\frac{2}{2}\) = 1
b² = a² (e² – 1) = 1(4 – 1) = 3
Equation of the hyperbola is
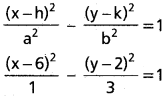
Multiplying with 3
3(x – 6)² – (y – 2)² = 3
⇒ 3(x² – 12x + 36) – (y² – 4y + 4) = 3
⇒ 3x² – 36x + 108 – y² + 4y – 4 -3 = 0
3x² – y² – 36x + 4y + 101 = 0
Question 3.
Find the equation of the hyperbola of given length of transverse axis 6 whose vertex bisects the distance between the centre and the focus.
Solution:
Given CA = AS
![]()
a = ae – a
2a = ae ⇒ e = 2
Length of transverse axis = 2a = 6 ⇒ a = 3
b² = a²(e² – 1) = 9(4 – 1) = 27
Equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1
\(\frac{x^2}{9}-\frac{y^2}{27}\) = 1
3x² – y² = 27
Question 4.
Find the equations of the tangents to the hyperbola x² – 4y² = 4 Which are i) Parallel ii) Perpendicular to the line x + 2y = 0.
Solution:
Equation of the hyperbola is x² – 4y² = 4
\(\frac{x^2}{4}-\frac{y^2}{1}\) = 1
a² = 4, b² = 1
i) The+anget is parallel to x + 2y = 0
m = –\(\frac{1}{2}\)
c² = a²m² – b² = 4.\(\frac{1}{4}\) – 1 = 1 – 1 = 0
c = 0
Equation of the parallel tangent is
y = mx + c
= –\(\frac{1}{2}\)x
2y = -x
x + 2y = 0.
ii) The tangent is perpendicular to x +2y = 0
Slope of the tangent = m = \(\frac{-1}{\left(-\frac{1}{2}\right)}\) = 2
c² = a²m² – b² = 4. 4 – 1 = 16
c = ±√15
Equation of the perpendicular tangent is
y = 2x ± √15
Question 5.
Find the equations of tangents drawn to the hyperbola 2x² – 3y² = 6 through (-2, 1).
Solution:
Equation of the hyperbola is 2x² – 3y² = 6
\(\frac{x^2}{3}-\frac{y^2}{2}\) = 1
Suppose the slope of the tangent is m¹
The tangent passes through P (-2, 1)
Equation of the tangent is
y – 1 = m(x + 2) = mx + 2m
y = mx + (2m + 1) ………. (1)
Condition for tangency is c² = a²m² – b²
(2m + 1)² = 3m² – 2
4m² + 4m + 1 = 3m² – 2
m² + 4 m + 3 = 0
(m + 1) (m + 3) = 0
m = -1 or – 3
Case (i): m = -1
Substituting in (1) equation of the tangent is
y = -x – 1
x + y + 1 =0
Case (ii) : m = – 3
Equation of the tangent is
y = – 3x – 5
3x + y + 5 = 0
Question 6.
Prove that the product of the perpendicular distance from any point on a hyperbola to its asymptotes is constant.
Solution:
Equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1
Any point on the hyperbola is P(a sec θ, b tan θ)
Equations of the asymptotes are \(\frac{x}{a}\) = ± \(\frac{y}{b}\)
i.e., \(\frac{x}{a}-\frac{y}{b}\) = 0 and \(\frac{x}{a}+\frac{y}{b}\) = 0
PM = Perpendicular distance from P on
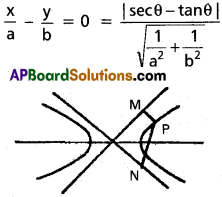
PN = Perpendicular distance from P on
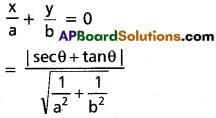
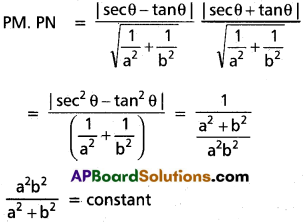
III.
Question 1.
Tangents to the hyperbola make angles \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 make angles θ1, θ2 with transverse axis of a hyperbola. Show that the point of intersection of these tangents lies on the curve 2xy = k(x² – a²) when tan θ1 + tan θ2 = k.
Solution:
Equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1
Equation of the tangent to the hyperbola can be taken as
y = mx ± \(\sqrt{a^2m^2-b^2}\)
Suppose p(x1, y1) is the point of intersection of the tangents
y1 = mx1 ± \(\sqrt{a^2m^2-b^2}\)
y1 – mx1 = ±\(\sqrt{a^2m^2-b^2}\)
Squaring both sides
(y1 – mx1)² = a²m² – b²
y²1 + m²x²1 – 2mx1y1 – a²m² + b² = 0
m² (x²1 – a²) – 2mx1y1 + (y²1 + b²) = 0
This is a quadratic equation in m giving the values for m say m1, m2
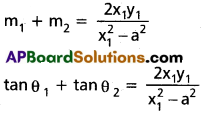
i.e.,k = \(\frac{2x_1y_1}{x^2_1-a^2}\)
or 2x1y1 = k(x²1 – a²1)
p(x1, y1) lies on the curve 2xy = k(x² – a²)
Question 2.
Show that the locus of feet of the perpen-diculars drawn from foci to any tangent of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 is the auxiliary circle of the hyperbola.
Solution:
Equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1
Equation of the tangent to the hyperbola is
y = mx ± \(\sqrt{a^2m^2-b^2}\)
y – mx = ± \(\sqrt{a^2m^2-b^2}\) ………… (1)
Equation to the perpendicular from foci (±ae, 0) on this tangent is 1
y = –\(\frac{1}{m}\)(x ± ae)
⇒ my = – (x ± ae)
x + my = ±ae …………. (2)
Squaring and adding (1) and (2)
(y – mx)² + (x + my)² = a²m² – b² + a²e²
⇒ y² + m²x² – 2mxy + x² + m²y² + 2mxy
= a²m² – a²(e² – 1) + a²e² .
⇒ (x² + y²) (1 + m²) = a²m² – a²e² + a² + a²e²
= a²(1 + m²)
or x² + y² = a² which is the auxiliary circle.
Locus of the feet of the perpendiculars drawn from the foci to any tangent to the hyperbola lies on the auxiliary circle.
Question 3.
Show that the equation \(\frac{x^2}{9-c}-\frac{y^2}{5-c}\) = 1 represents.
i) An ellipse if ‘c’ is a real constant less than 5.
ii) A hyperbola if ‘c’ is any real constant between 5 and 9.
iii) Show that each ellipse in (i) and each hyperbola (ii) has foci at the two points (±2, 0) independent of the value of ‘c’.
i) An ellipse if ‘c’ is a real constant less than 5.
Solution:
Given equation is
\(\frac{x^2}{9-c}-\frac{y^2}{5-c}\) = 1
This equation represents an ellipse if 9 – c >0, 5 – c > 0
∴ c < 9, c < 5
⇒ c < 5
ii) A hyperbola if ‘c’ is any real constant between 5 and 9.
Solution:
Given equation is \(\frac{x^2}{9-c}-\frac{y^2}{5-c}\) = 1
This equation represents a hyperbola if
9 – c > 0 and 5 – c < 0
9 > c and 5 < c
ic. 5 < c < 9
iii) Show that each ellipse in (i) and each hyperbola (ii) has foci at the two points (±2, 0), independent of the value ‘c’.
Solution:
In both cases
Case (i): a² = 9 – c, b² = 5 – c
a² – b² = (9 – c) – (5 – c)
= 9 – c – 5 + c = 4
a²e² = 4 ⇒ ae = 2
Foci are (±ae, 0) (±2, 0)
Case (ii) : a² = 9 – c, b² = c – 5
a² + b² = 9 – c + c – 5 = 4
a²e² = 4 ⇒ ae = 2
Foci are (± ae, 0) = (± 2, 0)
![]()
Question 4.
Show that the angle between two asymptotes of a hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 is 2 Tan-1(\(\frac{b}{a}\)) Or 2 Sec-1(e).
Solution:
Equations of the asymptotes are \(\frac{x}{a}-\frac{y}{b}\) = 0
and \(\frac{x}{a}+\frac{y}{b}\) = 0
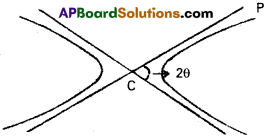
If 2 θ is the angle between the asymptotes then tan θ = \(\frac{b}{a}\) = slope of the asymptotes of θ = tan-1\(\frac{b}{a}\)
Angle between the asymptotes

Angle between the asymptotes
= 2tan-1\(\frac{b}{a}\) or 2 Sec-1(e)