Students get through Maths 2B Important Questions Inter 2nd Year Maths 2B Hyperbola Important Questions which are most likely to be asked in the exam.
Intermediate 2nd Year Maths 2B Hyperbola Important Questions
Question 1.
Find the equations of the hyperbola whose foci are (±5, 0) the transverse axis is of length 8. [T.S. Mar. 16; May 11]
Solution:
Foci are S(±5,0) ∴ ae = 5
Length of transverse axis = 2a = 8
a = 4
e = \(\frac{5}{4}\)
b2 = a2(e2 – 1) = 16(\(\frac{25}{16}\) – 1) = 9
Equation of the hyperbola is \(\frac{x^{2}}{16}\) – \(\frac{y^{2}}{9}\) = 1
9x2 – 16y2 = 144.
![]()
Question 2.
If the eccentricity of a hyperbola is \(\frac{5}{4}\), then find the eccentricity of its conjugate-hyperbola. [AP Mar. 16] [TS Mar. 15, 13]
Solution:
If e and e1, are the eccentricity of a hyper bola and its conjugate hyperbola, then
\(\frac{1}{\mathrm{e}^{2}}\) + \(\frac{1}{\mathrm{e}_{1}^{2}}\) = 1
Given e = \(\frac{5}{4}\) = \(\frac{16}{25}\) + \(\frac{1}{\mathrm{e}_{1}^{2}}\) = 1
\(\frac{1}{\mathrm{e}_{1}^{2}}\) = 1 – \(\frac{16}{25}\) = \(\frac{9}{25}\) e12 = \(\frac{25}{9}\)
e1 = \(\frac{5}{3}\)
Question 3.
Find the centre, foci, eccentricity equation of the directrices, length of the latus rectum of the x2 – 4y2 = 4 hyperbola. [A.P. Mar. 16; May 11]
Solution:
Equation of the hyperbola is \(\frac{x^{2}}{4}\)– \(\frac{y^{2}}{1}\) = 1
a2 = 4, b2 = 1
Centre is c (0, 0)
a2e2 = a2 + b2 = 4 + 1 = 5
ae = \(\sqrt{5}\)
Foci are (±ae, 0) = (±\(\sqrt{5}\), 0)
Eccentricity = \(\frac{\mathrm{ae}}{\mathrm{a}}\) = \(\frac{\sqrt{5}}{2}\)
Equations of directrices are x = ± \(\frac{\mathrm{ae}}{\mathrm{a}}\)
= ± 2 . \(\frac{2}{\sqrt{5}}\)
⇒ \(\sqrt{5}\) x = ± 4
⇒ \(\sqrt{5}\) x ± 4 = 0
Length of the latus rectum = \(\frac{2 b^{2}}{a}\) = \(\frac{2.1}{2}\) = 1
![]()
Question 4.
Find the equations of the tangents to the hyperbola 3x2 – 4y2 = 12 which are
i) Parallel and
ii) Perpendicular to the line y = x – 7. [AP Mar. 15]
Solution:
i) Equation of the hyperbola is 3x2 – 4y2 = 12
\(\frac{x^{2}}{4}\) – \(\frac{y^{2}}{3}\) = 1
a2 = 4, b2 = 3.
The tangent is parallel to y = x – 7
m = slope of the tangent = 1
Equation of the parallel tangents are
y = mx ± \(\sqrt{a^{2} m^{2}-b^{2}}\)
y = x ± \(\sqrt{4-3}\)
y = x ± 1
ii) The tangent is perpendicular to y – x = 7
m – slope of the tangent = (-1)
Equation of the perpendicular tangents are
y = (-1) x ± \(\sqrt{4(-1)^{2}-3}\)
= -x ± 1
x + y = ± 1.
Question 5.
If 3x – 4y – k = 0 is a tangent to x2 – 4y2 = 5, find value of k. [T.S. Mar. 17]
Solution:
Equation of the hyperbola x2 – 4y2 = 5
\(\frac{x^{2}}{5}\) – \(\frac{y^{2}}{\left(\frac{5}{4}\right)}\) = 1
a2 = 5, b2 = \(\frac{5}{4}\)
Equation of the given line is 3x — 4y + k = 0
4y = 3x + k
y = \(\frac{3}{4}\) x + \(\frac{k}{4}\)
m = \(\frac{3}{4}\), c = \(\frac{k}{4}\),
Condition for tangency is c2 = a2m2 – b2
\(\frac{\mathrm{k}^{2}}{16}\) = 5 . \(\frac{9}{16}\) – \(\frac{5}{4}\)
k2 = 45 – 20 = 25
k = ± 5.
![]()
Question 6.
Find the equations of the tangents to the hyperbola x2 – 4y2 = 4 Which are
i) Parallel
ii) Perpendicular to the line x + 2y = 0. [T.S. Mar. 15, Mar. 14, 11; May 06]
Solution:
Equation of the hyperbola is
x2 – 4y2 = 4
\(\frac{x^{2}}{4}\) – \(\frac{y^{2}}{1}\) = 1
a2 = 4, b2 = 1
i) The tangent is parallel to x + 2y = 0
m = –\(\frac{1}{2}\)
c2 = a2m2 – b2 = 4 . \(\frac{1}{4}\) = 1 – 1 = 0
c = 0
Equation of the parallel tangent is
y = mx + c
= –\(\frac{1}{2}\) x
2y = -x
x + 2y = 0.
ii) The tangent is perpendicular to x + 2y = 0
Slope of the tangent = m = \(\frac{-1}{\left(-\frac{1}{2}\right)}\) = 2
c2 = a2m2 – b2 = 4 . 4 – 1 = 153
c = ±\(\sqrt{15}\)
Equation of the perpendicular tangent is
y = 2x ± \(\sqrt{15}\)
Question 7.
Prove that the point of intersection of two perpendicular tangents to the hyperbola \(\frac{x^{2}}{a^{2}}\) – \(\frac{y^{2}}{b^{2}}\) = 1 lies on the circle x2 + y2 = a2 – b2. [T.S. Mar. 16]
Solution:
Let P (x1, y1) be the point of intersection of two perpendicular tangents to the hyperbola
\(\frac{x^{2}}{a^{2}}\) – \(\frac{x^{2}}{b^{2}}\) = 1
Equation of the tangent can be taken as
y = mx ± \(\sqrt{a^{2} m^{2}-b^{2}}\)
This tangent passes through P (x1, y1)
y1 = mx1 ± \(\sqrt{a^{2} m^{2}-b^{2}}\)
(y1 – mx1)2 = a2m2 – b2
y12 + m2x12 – 2mx1y1 = a2m2 – b2
m2x12 – a2m2 – 2mx1y1 + y12 + b2 = 0
m2(x12 – a2) – 2mx1y1 + (y12 + b2) = 0
This is a quadratic in m giving the values say m1, m1 which are the slopes of the tangents
passing through P
The tangents are perpendicular
⇒ m1m2 = – 1
\(\frac{y_{1}^{2}+b^{2}}{x_{1}^{2}-a^{2}}\) = – 1 ⇒ y12 + b2
x12 + y12 = a2 – b2
focus of P (x1, y1) is x2 + y2 = a2 – b2.
This circle is called director circle of the hyperbola.
![]()
Question 8.
If e, e1 are the eccentricities of a hyperbola and its conjugate hyperbola prove that \(\frac{1}{e^{2}}\) + \(\frac{1}{\mathrm{e}_{1}^{2}}\) = 1 [Mar. 11]
Solution:
Equation of the hyperbola is \(\frac{x^{2}}{a^{2}}\) – \(\frac{x^{2}}{b^{2}}\) = 1
∴ b2 = a2(e2 – 1) ⇒ e2 – 1 = \(\frac{b^{2}}{a^{2}}\)
e2 = 1 + \(\frac{b^{2}}{a^{2}}\) = \(\frac{a^{2}+b^{2}}{a^{2}}\)
∴ \(\frac{1}{\mathrm{e}^{2}}\) = \(\frac{a^{2}}{a^{2}+b^{2}}\) …………… (1)
Equation of the conjugate hyperbola is

Question 9.
Find the centre eccentricity, foci, directrices and length of the latus rectum of the following hyperbolas.
i) 4x2 – 9y2 – 8x – 32 = 0
ii) 4 (y + 3)2 – 9(x – 2)2 = 1.
Solution:
i) 4x2 – 9y2 – 8x – 32 = 0
4(x2 – 2x) – 9y2 = 32
4(x2 – 2x + 1) – 9y2 = 36
\(\frac{(x-1)^{2}}{9}\) – \(\frac{(y)^{2}}{4}\) = 1
Centre of the hyperbola is C (1, 0)
a2 = 9, b2 = 4 ⇒ a = 3, b = 2
e = \(\sqrt{\frac{a^{2}+b^{2}}{a^{2}}}=\sqrt{\frac{9+4}{9}}=\frac{\sqrt{13}}{3}\)
Foci are (1±3. \(\frac{\sqrt{13}}{3}\), 0) = (1±\(\sqrt{13}\), 0)
Equations of differences are x = 1 ± \(\frac{3.3}{\sqrt{13}}\)
⇒ x = 1 ± \(\frac{9}{\sqrt{13}}\)
Length of the latus rectum = \(\frac{2 b^{2}}{a}\)
= \(\frac{2.4}{3}\) = \(\frac{8}{3}\)
ii) The equation of the hyperbola is
4 (y + 3)2 – 9 (x – 2)2 = 1
\(\frac{y-(-3)^{2}}{1 / 4}\) = \(\frac{(x-2)^{2}}{1 / 9}\) = 1
Centre is C (2, -3)
Semi transverse axis = b = \(\frac{1}{2}\)
Semi conjugate axis = a = \(\frac{1}{3}\)

Question 10.
If e, e1 are the eccentricities of a hyperbola and its conjugate hyperbola prove that \(\frac{1}{e^{2}}\) + \(\frac{1}{e_{1}^{2}}\) = 1. [Mar. 11]
Solution:

Equation of the conjugate hyperbola is
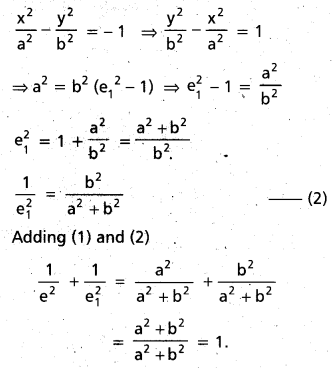
![]()
Question 11.
i) If the line lx + my = 0 is a tangent to the hyperbola \(\frac{x^{2}}{a^{2}}\) – \(\frac{y^{2}}{b^{2}}\) = 1, then show that a2l2 – b2m2 = n2.
ii) If the lx + my = 1 is a normal to the hyperbola \(\frac{x^{2}}{a^{2}}\) – \(\frac{y^{2}}{b^{2}}\) = 1, then show that \(\frac{a^{2}}{l^{2}}\) – \(\frac{b^{2}}{m^{2}}\) = (a2 + b2)2.
Solution:
i) Equation of the given tangent ¡s
lx + my + n = 0 ……………. (1)
Equation of the tangent P(θ) is
\(\frac{x}{a}\) sec θ – \(\frac{y}{b}\) tan θ – 1 = 0 …………….. (2)
Comparing (1) and (2)
\(\frac{\sec \theta}{a l}\) = \(\frac{\tan \theta}{-\mathrm{bm}}\) = \(\frac{-1}{n}\)
sec θ = –\(\frac{\mathrm{a} l}{\mathrm{n}}\), tan θ = \(\frac{\mathrm{bm}}{\mathrm{n}}\)
sec2 θ – tan2θ = 1
= \(\frac{a^{2} l^{2}}{n^{2}}\) – \(\frac{b^{2} m^{2}}{n^{2}}\) = 1 ⇒ a2l2 – b2m2 = n2.
ii) Equation of the given line is lx + my = 1 ……………. (1)
Equation of the normal at P(θ) is
\(\frac{a x}{\sec \theta}\) + \(\frac{b y}{\tan \theta}\) = a2 + b2 ……….. (2)
Comparing (1) and (2)

Question 12.
Find the equations of the tangents to the hyperbola 3x2 – 4y2 = 12 which are
i) Parallel and ii) Perpendicular to the line y = x – 7. [A.P. Mar. 15]
Solution:
i) Equation of the hyperbola is 3x2 – 4y2 = 12
\(\frac{x^{2}}{4}\) – \(\frac{y^{2}}{3}\) = 1
a2 = 4, b2 = 3
The tangent is parallel to y = x – 7
m = slope of the tangent = 1
Equation of the parallel tangents are
y = mx ± \(\sqrt{a^{2} m^{2}-b^{2}}\)
y = x ± \(\sqrt{4-3}\)
y = x ± 1
ii) Th tangent is perpendicular to y – x = 7
m – slope of the tangent = (-1)
Equation of the perpendicular tangents are
y = (-1) x ± \(\sqrt{4(-1)^{2}-3}\)
= -x ± 1
x + y = ±1.
![]()
Question 13.
Prove that the point of intersection of two perpendicular tangents to the hyperbola \(\frac{x^{2}}{a^{2}}\) – \(\frac{y^{2}}{b^{2}}\) = 1 lies on the circle x2 + y2 = a2 – b2. [T.S. Mar. 16]
Solution:
Let P (x1, y1) be the point of intersection of two perpendicular tangents to the hyperbola
\(\frac{x^{2}}{a^{2}}\) – \(\frac{y^{2}}{b^{2}}\) = 1
Equation of the tangent can be taken as
y = mx ± \(\sqrt{a^{2} m^{2}-b^{2}}\)
This tangent passes through P (x1, y1)
y1 = mx1 ± \(\sqrt{a^{2} m^{2}-b^{2}}\)
(y1 – mx1)2 = a2m2 – b2
y12 + m2x12 – 2mx1y1 = a2m2 – b2
m2x12 – a2m2 – 2mx1y1 + y12 + b2 = 0
m2 (x12 – a2) – 2mx1y1 + (y12 + b2) = 0
This is a quadratic in m giving the values say m1, m2 which are the slopes of the tangents passing through P
The tangents are perpendicular
⇒ m1m2 = – 1
\(\frac{y_{1}^{2}+b^{2}}{x_{1}^{2}-a^{2}}\) = -1 ⇒ y12 + b2 = -x12 + a2
x12 + y12 = a2 – b2
focus of P (x1, y1) is x2 + y2 = a2 – b2.
This circle is called director circle of the hyperbola.
Question 14.
A circle cuts the rectangular hyperbola xy = 1 in the points (xr, yr), r = 1, 2, 3, 4. Prove that x1x2x3x4 = y1y2y3y4 = 1.
Solution:
Let the circle be x2 + y2 = a2.
Since (t, \(\frac{1}{t}\)) (t ≠ 0) lies on xy = 1, the points of intersection of the circle and the hyperbola are given by
t2 + \(\frac{1}{t^{2}}\) = a2
⇒ t4 – a2t2 + 1 = 0
⇒ t4 + 0 . t3 – a2t2 + 0 . t + 1 = 0.
If t1, t2, t3 and t4 are the roots of the above biquadratic, then t1t2t3t4 = 1.
If (xr, yr) = (tr; \(\frac{1}{t_{r}}\)), r = 1, 2, 3, 4
then x1x2x3x4 = t1t2t3t4 = 1,
and y1y2y3y4 = \(\frac{1}{t_{1} t_{2} t_{3} t_{4}}\) = 1
![]()
Question 15.
If four points be taken on a rectangular hyperbola such that the chords joining any two points is perpendicular to the chord joining the other two, and if α, β, γ and δ be the inclinations to either asymptote of the straight lines joining these points to the centre, prove that
tan α tan β tan γ tan δ = 1.
Solution:
Let the equation of the rectangular hyperbola be x2 – y2 = a2. By rotating the X-axis and the Y-axis about the origin through an angle \(\frac{\pi}{4}\) in the clockwise sense, the equation x2 – y2 = a2 can be transformed to the form xy = c2.
Let (ctr, \(\frac{c}{t_{r}}\)), r = 1, 2, 3, 4 (tr ≠ 0) be four point on the curve. Let the chord joining
A = (ct1, \(\frac{c}{t_{1}}\)), B = (ct2, \(\frac{c}{t_{2}}\)) be perpendicular to the chord joining C = (ct3, \(\frac{c}{t_{3}}\)) and D = (ct4, \(\frac{c}{t_{4}}\)).
The slope of \(\stackrel{\leftrightarrow}{A B}\) is \(\frac{\frac{c}{t_{1}}-\frac{c}{t_{2}}}{c t_{1}-c t_{2}}=\frac{-1}{t_{1} t_{2}}\)
[No chord of the hyperbola can be vertical]
Similarly slope of \(\stackrel{\leftrightarrow}{C D}\) is –\(\frac{1}{t_{3} t_{4}}\), Since \(\stackrel{\leftrightarrow}{A B}\) ⊥ \(\stackrel{\leftrightarrow}{C D}\).
\(\left(-\frac{1}{t_{1} t_{2}}\right)\left(-\frac{1}{t_{3} t_{4}}\right)\) = -1 ⇒ t1t2t3t4 = -1 ………………… (1)
We know the coordinate axes are the asymptotes of the curve, If \(\stackrel{\leftrightarrow}{\mathrm{OA}}\), \(\stackrel{\leftrightarrow}{\mathrm{OB}}\), \(\stackrel{\leftrightarrow}{\mathrm{OC}}\) and \(\stackrel{\leftrightarrow}{\mathrm{OD}}\) make angles α, β, γ and δ with the positive direction of the X-axis, then tan α, tan β, tan γ and tan δ are their respective slopes. [O, the origin is the centre, None of \(\stackrel{\leftrightarrow}{\mathrm{OA}}\), \(\stackrel{\leftrightarrow}{\mathrm{OB}}\), \(\stackrel{\leftrightarrow}{\mathrm{OC}}\) and \(\stackrel{\leftrightarrow}{\mathrm{OD}}\) is vertical]

If \(\stackrel{\leftrightarrow}{\mathrm{OA}}\), \(\stackrel{\leftrightarrow}{\mathrm{OB}}\), \(\stackrel{\leftrightarrow}{\mathrm{OC}}\) and \(\stackrel{\leftrightarrow}{\mathrm{OD}}\) make angles α, β, γ and δ with the other asymptote the Y-axis then cot α, cot β, cot γ and cot δ are their respective inclinations so that
cot α cot β cot γ cot δ = tan α tan β tan γ tan δ = 1.