Use these Inter 2nd Year Maths 2B Formulas PDF Chapter 5 Hyperbola to solve questions creatively.
Intermediate 2nd Year Maths 2B Hyperbola Formulas
Definition:
A conic with eccentricity greater than one is called a hyperbola, i.e., the locus of a point, the ratio of whose distances from a fixed point (focus) and fixed straight line (directrix) is e, where e> 1 is called hyperbola.
Equation of hyperbola in standard form:
→ \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1
Here b2 = a2 (e2 – 1)
→ The difference of the focal distances of any point on the hyperbola is constant.
(i.e.,) SP ~ S’P = 2a
![]()
→ A Point P(x1, y1) in the plane of the hyperbola S = 0 lies inside the hyperbola, if S11 < 0, lies outside if S11 > 0 and on the curve S11 = 0
→ Ends of the latus rectum (± ae, ± b2/a) and the length of the latus rectum is 2b2/a.
→ Equation of tangent at P(x1, y1) to \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1
\(\frac{x x_{1}}{a^{2}}-\frac{y y_{1}}{b^{2}}\) = 1
→ Equation of normal at P(x1, y1)
\(\frac{a^{2} x}{x_{1}}+\frac{b^{2} y}{y_{1}}\) = a2 + b2
→ Parametric form is x = a sec θ, y = b tan θ.
→ Equation of tangent at ‘θ’ on the hyperbola
\(\frac{x}{a}\) sec θ – \(\frac{y}{b}\) tan θ = 1
→ Equation of normal at θ on the hyperbola
\(\frac{a x}{\sec \theta}+\frac{b y}{\tan \theta}\) = a2 + b2
→ A necessary and sufficient condition for a straight line y = mx + c to be tangent to hyperbola c2 = a2m2 – b2
y = mx ± \(\sqrt{a^{2} m^{2}-b^{2}}\)
→ If P(x1, y1) is any point in the plane of the hyperbola S = 0 then the equation of the polar of P is S1 = 0.
![]()
→ The pole of the line lx + my + n = 0; n ≠ 0 with respect to the hyperbola S = 0 is
\(\left(\frac{-a^{2} l}{n} ; \frac{b^{2} m}{n}\right)\), n ≠ 0
Equation of a Hyperbola in Standard From.
The equation of a hyperbola in the standard form is \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.
Proof:
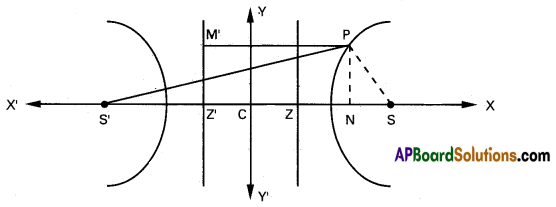
Let S be the focus, e be the eccentricity and L = 0 be the directrix of the hyperbola.
Let P be a point on the hyperbola. Let M, Z be the projections of P, S on the directrix L = 0 respectively. Let N be the projection of P on SZ. Since e > 1, we can divide SZ both internally and externally in the ratio e : 1.
Let A, A’ be the points of division of SZ in the ratio e : 1 internally and externally respectively. Let AA’ = 2a. Let C be the midpoint of AA’. The points A, A’ lie on the hyperbola and \(\frac{\mathrm{SA}}{\mathrm{AZ}}\) = e, \(\frac{\mathrm{SA}^{\prime}}{\mathrm{A}^{\prime} \mathrm{Z}}\) = e
∴ SA = eAZ, SA’ = eA’Z
Now SA + SA’ = eAZ + eA’Z
⇒ CS – CA + CS + CA’ = e(AZ + A’Z)
⇒ 2CS = eAA’ (∵ CA = CA’)
⇒ 2CS = e2a ^ CS = ae
Aslo SA’ – SA = eA’Z – eAZ
AA’ = e(A’Z – AZ)
⇒ 2a = e[CA’ + CZ – (CA – CZ)]
⇒ 2a = e 2CZ (∵ CA = CA’) ⇒ CZ = \(\frac{a}{e}\).
Take CS, the principal axis of the hyperbola as
x-axis and Cy perpendicular to CS as y-axis. Then S = (ae, 0).
Let P(x1, y1).
Now PM = NZ = CN – CZ = x1 – \(\frac{a}{e}\).
P lies on the hyperbola ⇒ \(\frac{\mathrm{PS}}{\mathrm{PM}}\) = e
⇒ PS = ePM ⇒ PS2 = e2PM2
⇒ (x1 – ae)2 + (y1 – 0)2 = e2 \(\left(x_{1}-\frac{a}{e}\right)^{2}\)
⇒ (x1 – ae)2 + y12 = (x1e – a)2
⇒ x12 + a2 e2 – 2x1ae + y12 = x1e2 + a2 – 2x1ae
⇒ x2(e2 -1) – y2 = a2(e2 -1)
⇒ \(\frac{x_{1}^{2}}{a^{2}}-\frac{y_{1}^{2}}{a^{2}\left(e^{2}-1\right)}\) = 1 ⇒ \(\frac{x_{1}^{2}}{a^{2}}-\frac{y_{1}^{2}}{b^{2}}\) = 1
Where b2 = a2(e2 – 1)
The locus of P is \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.
The equation of the hyperbola is \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.
Nature of the curve \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1
Let C be the curve represented by \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1. Then
(i) (x,y) ∈ C(x, -y) ∈ C and (x, y) ∈ C ⇔ (-x,y) ∈ C.
Thus the curve is symmetric with respect to both the x-axis and the y-axis. Hence the coordinate axes are two axes of the hyperbola.
(ii) (x, y) ∈ C ⇔ (-x, -y) ∈ C.
Thus the curve is symmetric about the origin O and hence O is the midpoint of every chord of the hyperbola through O. Therefore the origin is the center of the hyperbola.
(iii) (x, y) ∈ C and y = 0 ⇒ x2 = a2 ⇒ x = ±a.
Thus the curve meets x-axis (Principal axis) at two points A(a, 0), A'(-a, 0). Hence hyperbola has two vertices. The axis AA’ is called transverse axis. The length of transverse axis is AA’ = 2a.
(iv) (x, y) ∈ C and x = 0 ⇒ y2 = -b2 ⇒ y is imaginary.
Thus the curve does not meet the y-axis. The points B(0, b), B'(0, -b) are two points on y-axis. The axis BB’ is called conjugate axis. BB’ = 2b is called the length of conjugate axis.
(v) \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 ⇒ y = \(\frac{b}{a} \sqrt{x^{2}-a^{2}}\) ⇒ y has no real value for -a < x < a.
Thus the curve does not lie between x = -a and x = a.
Further x → ∞ ⇒ y ^ ± ∞ and
x → -∞ ⇒ y → ± ∞.
Thus the curve is not bounded (closed) on both the sides of the axes.
(vi) The focus of the hyperbola is S(ae, 0). The image of S with respect to the conjugate axis is S'(-ae, 0). The point S’ is called second focus of the hyperbola.
(vii) The directrix of the hyperbola is x = a/e. The image of x = a/e with respect to the conjugate axis is x = -a/e. The line x = -a/e is called second directrix of the hyperbola corresponding to the second focus S’.
![]()
Theorem:
The length of the latus rectum of the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 is \(\frac{2 b^{2}}{a}\)
Proof:
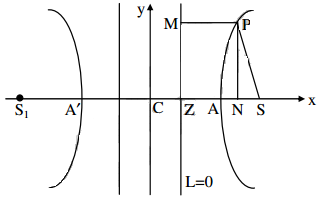
Let LL be the length of the latus rectum of the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.
If SL = 1, then L = (ae, 1)
L lies on the hyperbola ⇒ \(\frac{(a \mathrm{e})^{2}}{a^{2}}-\frac{1^{2}}{b^{2}}\) = 1
⇒ \(\frac{1^{2}}{\mathrm{~b}^{2}}\) = e2 – 1 ⇒ 12 = b2(e2 – 1)
⇒ 1 = b2 × \(\frac{\mathrm{b}^{2}}{\mathrm{a}^{2}}\) ⇒ 1 = \(\frac{b^{2}}{a}\) ⇒ SL = \(\frac{b^{2}}{a}\)
∴ LL’ = 2SL = \(\frac{2 b^{2}}{a}\)
Theorem:
The difference of the focal distances of any point on the hyperbola is constant f P is appoint on the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 with foci S and S then |PS’- PS| = 2a
Proof:
Let e be the eccentricity and L = 0, L’ = 0 be the directrices of the hyperbola.
Let C be the centre and A, A’ be the vertices of the hyperbola.
∴ AA’ = 2a
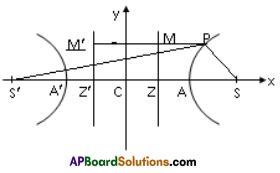
Foci of the hyperbola are S(ae, 0), S'(-ae, 0).
Let P(x1, y1) be a point on the hyperbola.
Let M, M’ be the projections of P on the directrices L = 0, L’ = 0 respectively.
∴ \(\frac{\mathrm{SP}}{\mathrm{PM}}\) = e, \(\frac{\mathrm{S}^{\prime} \mathrm{P}}{\mathrm{PM}^{\prime}}\) = e
Let Z, Z’ be the points of intersection of transverse axis with directrices.
∴ MM’ = ZZ’ = CZ + CZ’ = 2a/e
PS’ – PS = ePM’ – ePM = e(PM’ – PM)
= e(MM’) = e(2a/e) = 2a
Notation: We use the following notation in this chapter.
S ≡ \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) – 1, S1 = \(\frac{x_{1}}{a^{2}}-\frac{y_{1}}{b^{2}}\) – 1
S11 ≡ S(x1, y1) = \(\frac{x_{1}^{2}}{a^{2}}-\frac{y_{1}^{2}}{b^{2}}\) – 1, S12 = \(\frac{\mathrm{x}_{1} \mathrm{x}_{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}_{1} \mathrm{y}_{2}}{\mathrm{~b}^{2}}\) – 1
Note: Let F(x1, y1) be a point and S ≡ \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) – 1 = 0 be a hyperbola. Then
- F lies on the hyperbola S = 0 ⇔ S11 = 0
- F lies inside the hyperbola S = 0 ⇔ S11 > 0
- F lies outside the hyperbola S = 0 ⇔ S11 < 0
Theorem:
The equation of the chord joining the two points A(x1, y1), B(x2, y2) on the hyperbola S = 0 is S1 + S2 = S12.
Theorem:
The equation of the normal to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 at P(x1 y1) is \(\frac{\mathrm{a}^{2} \mathrm{x}}{\mathrm{x}_{1}}+\frac{\mathrm{b}^{2} \mathrm{y}}{\mathrm{y}_{1}}\) = a2 + b2.
Theorem: The condition that the line y = mx + c may be a tangent to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 is c2 = a2m2 – b2
Note: The equation of the tangent to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 may be taken as y = mx ± \(\sqrt{a^{2} m^{2}-b^{2}}\)
The point of contact is \(\left(\frac{-a^{2} m}{c}, \frac{-b^{2}}{c}\right)\) where c = am – b
Theorem: Two tangents can be drawn to a hyperbola from an external point.
Note: If m1, m2 are the slopes of the tangents through P, then m1 m2 become the roots of (x22 – a2)m2 – 2x1y1m + (y12 + b2) = 0
Hence m1 + m2 = \(\frac{2 \mathrm{x}_{1} \mathrm{y}_{1}}{\mathrm{x}_{1}^{2}-\mathrm{a}^{2}}\)
m1m2 = \(\frac{\mathrm{y}_{1}^{2}+\mathrm{b}^{2}}{\mathrm{x}_{1}^{2}-\mathrm{a}^{2}}\)
Theorem:
The point of intersection of two perpendicular tangents to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 lies on the circle x2 + y2 = a2 – b2.
Proof:
Equation of any tangent to the hyperbola is:
y = mx ± \(\)
Suppose P(x1, y1) is the point of intersection of tangents.
Plies on the tangent Y1 = mx1 ± \(\sqrt{a^{2} m^{2}-b^{2}}\) y1 = mx1 = ±\(\sqrt{a^{2} m^{2}-b^{2}}\)
= (y1 – mx1)2 = a2m2 – b2
y12 + m2x12 – 2mx1y1 – a2m2 + b2 = 0
= m2(x12 – a2) – 2mx1y1 + (y12 + b2) = 0
This is a quadratic in m giving the values for m say m1 and m2.
The tangents are perpendicular
⇒ m1m2 = -1 ⇒ \(\frac{\mathrm{y}_{1}^{2}+\mathrm{b}^{2}}{\mathrm{x}_{1}^{2}-\mathrm{a}^{2}}\) = -1
⇒ y12 + b2 = -x2 + a2 ⇒ x12 + y12 = a2 – b2
P(x1, y1) lies on the circle x2 + y = a2 – b2.
![]()
Definition:
The point of intersection of perpendicular tangents to a hyperbola lies on a circle, concentric with the hyperbola. This circle is called director circle of the hyperbola.
Corollary:
The equation to the auxiliary circle of \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\)= 1 is x2 + y2 = a2.
Theorem:
The equation to the chord of contact of P(x1, y1) with respect to the hyperbola S = 0 is S1 = 0.
Midpoint of a Chord:
Theorem: The equation of the chord of the hyperbola S = 0 having P(x1, y1) as it’s midpoint is S1 = S11.
Pair of Tangents:
Theorem: The equation to the pair of tangents to the hyperbola S = 0 from P(x1, y1) is S12 = S11S
Asymptotes:
Definition: The tangents of a hyperbola which touch the hyperbola at infinity are called asymptotes of the hyperbola.
Note:
- The equation to the pair of asymptotes of \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 is \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 0.
- The equation to the pair of asymptotes and the hyperbola differ by a constant.
- Asymptotes of a hyperbola passes through the centre of the hyperbola.
- Asymptotes are equally inclined to the axes of the hyperbola.
- Any straight line parallel to an asymptote of a hyperbola intersects the hyperbola at only one point.
Theorem:
The angle between the asymptotes of the hyperbola S = 0 is 2tan-1(b/a).
Proof:
The equations to the asymptotes are y = ± \(\frac{b}{a}\)x.
If θ is an angle between the asymptotes, then
tan θ = \(\frac{\frac{\mathrm{b}}{\mathrm{a}}-\left(-\frac{\mathrm{b}}{\mathrm{a}}\right)}{1+\left(\frac{\mathrm{b}}{\mathrm{a}}\right)\left(-\frac{\mathrm{b}}{\mathrm{a}}\right)}=\frac{2\left(\frac{\mathrm{b}}{\mathrm{a}}\right)}{1-\frac{\mathrm{b}^{2}}{\mathrm{a}^{2}}}=\frac{2 \tan \alpha}{1-\tan ^{2} \alpha}\) = tan 2α Where tan α = \(\frac{b}{a}\)
∴ θ = 2α = 2Tan-1\(\frac{b}{a}\)
![]()
Parametric Equations:
A point (x, y) on the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 represented as x = a sec θ, y = b tan θ in a single parameter θ. These equations x = a sec0, y= b tan θ are called parametric equations of the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.
The point (a sec θ, b tan θ) is simply denoted by θ.
Note: A point on the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 can also be represented by (a cosh θ, b sinh θ). The equations x = a cosh θ, y = sinh θ are also called parametric equations of the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.
Theorem: The equation of the chord joining two points α and β on the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 is:
\(\frac{x}{a}\)cos\(\frac{\alpha-\beta}{2}\) – \(\frac{y}{b}\)sin\(\frac{\alpha+\beta}{2}\) = cos\(\frac{\alpha+\beta}{2}\)
Theorem:
The equation of the tangent at P(0) on the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 is \(\frac{x}{a}\)cos\(sec θ – [latex]\frac{y}{b}\) tan θ = 1.
Theorem:
The equation of the normal at P(0) on the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 is \(\frac{a x}{\sec \theta}+\frac{\text { by }}{\tan \theta}\) = a2 + b2.