Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Ellipse Solutions Exercise 4(a) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2B Ellipse Solutions Exercise 4(a)
I.
Question 1.
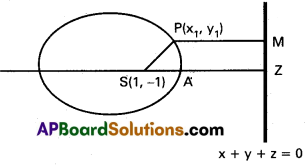
Find the equation of the ellipse with focus at (1, -1) e = \(\frac{2}{3}\) and directrix as x + y + 2 = 0.
Solution:
P(x1, y1) is any point on the ellipse. Equation of the directrix is
x + y + 2 = 0
Draw PM perpendicular to ZM, Join SP
By Definition of ellipse SP = e . PM
SP² = e². PM²

9[(x1 – 1)² + (y1 + 1)²] = 2[x1 + y1 + 2]²
9[x²1 – 2x1 + 1 + y²1 + 2y1 + 1] = 2[x²1 + y²1 + 4 + 2x1y1 + 4x1 + 4y1]
9x²1 +9y²1 – 18x1 18y1 +18 = 2x²1 +2y²1 + 4x1y1 + 8x1 + 8y1 + 8
7x²1 – 4x1y1 + 7y²1 – 26x1 + 10y1 +10 = 0 focus of P (x1, y1) is
7x² – 4xy + 7y² – 26x + 10y + 10 = 0
This is the equation of the required Ellipse.
Question 2.
Find the equation of the ellipse in the standard form whose distance between foci is 2 and the length of latus rectum is \(\frac{15}{2}\).
Solution:
Latus rectum = \(\frac{15}{2}\) ;
distance between foci = 2
\(\frac{2b^2}{2}\) = \(\frac{15}{2}\) ; 2ae = 2
ae = 1
⇒ b² = a² – a²e²
⇒ b² = a² – 1
⇒ \(\frac{15}{2}\)a = a² – 1
⇒ 4a² – 15a – 4 = 0
a = 4 or a = –\(\frac{1}{4}\)
b² = a² – 1
= 16 – 1
Equation of the ellipse is \(\frac{x^{2}}{16}+\frac{y^{2}}{15}\) = 1
![]()
Question 3.
Find the equation of the ellipse in the standard form such that distance between foci is 8 and distance between directrices is 32.
Solution:
Distance between foci = 8.
Distance between directrices = 32.
2ae = 8, \(\frac{2a}{e}\) = 32
ae = 4, \(\frac{a}{e}\) = 16
(ae)\(\frac{a}{e}\) = 64
a² = 64
b² = a² – a² e²
= 64 – 16 = 48
Equation of the ellipse is
∴ \(\frac{x^{2}}{64}+\frac{y^{2}}{48}\) = 1
Question 4.
Find the eccentricity of the ellipse, (in standard form), if its length Solution:
Latus rectum = \(\frac{2b^2}{a}\)
Major axis = 2a
Given \(\frac{2b^2}{a}\) = \(\frac{1}{2}\) .2a.
2b² = a²
But b² = a² (1 – e²)
2a²(1 – e²) = a²
1 – e² = \(\frac{1}{2}\)
e² = \(\frac{1}{2}\) ⇒ e = \(\frac{1}{\sqrt{2}}\)
![]()
Question 5.
The distance of a point on the ellipse x² + 3y² = 6 from its centre is equal to 2. Find the eccentric angles.
Solution:
Equation of the ellipse is x² + 3y² = 6
\(\frac{x^{2}}{6}+\frac{y^{2}}{2}\)
a = √6 , b = √2
Any point on the ellipse is
P (√6 cos θ, √2 sin θ)
Given CP = 2 ⇒ CP² = 4
6 cos² θ + 2 sin² θ = 4
6(1 – sin² θ + 2 sin² θ = 4
6 – 6 sin² θ + 2 sin² θ = 4

Question 6.
Find the equation of ellipse in the standard form, if it passes through the points (-2, 2) and (3, -1).
Solution:
Equation of the ellipse in standard form is
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
passes through-(-2, 2); (3, -1)
\(\frac{4}{a^{2}}+\frac{4}{b^{2}}\) = 1 ……… (i)
\(\frac{9}{a^{2}}+\frac{1}{b^{2}}\) = 1 ……….(ii)
Solving (i) and (ii) we get
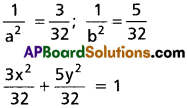
3x² + 5y² = 32.
Question 7.
If the ends of major axis of an ellipse are (5, 0) and (-5, 0). Find the equation of the ellipse in the standard form if its focus lies on the line 3x – 5y – 9 = 0.
Solution:
(a, 0): (5, 0), (-a, 0) : (-5, 0)
a = 5, b² = a² (1 – e²)
Focus lies on the line 3x – 5y – 9 = 0
3(ae) – 5 (0) – 9 = 0
3(5e) – 9 = 0

Equation of the ellipse is
\(\frac{x^{2}}{25}+\frac{y^{2}}{16}\) ⇒ 16x² + 25y² = 400
![]()
Question 8.
If the length of the major axis of an ellipse is three times the length of its minor axis then find the eccentricity of the ellipse.
Solution:
Major axis = 3 minor axes
2a = 3(2b) ⇒ a = 3b
a² = 9b² ⇒ a² = 9a² (1 – e²)
(1 – e²) = \(\frac{1}{9}\) ⇒ e² = 1 – \(\frac{1}{9}\) = \(\frac{8}{9}\)
e = \(\frac{2\sqrt{2}}{3}\)
Eccentricity of the ellipse = \(\frac{2\sqrt{2}}{3}\)
II.
Question 1.
Find the length of major axis, minor axis, latus rectum, eccentricity, co-ordinates of centre, foci and the equations of directrices of the following ellipse.
i) 9x² + 16y² = 144
ii) 4x² + y² – 8x + 2y + 1 =0
iii) x² + 2y² – 4x + 12y + 14 = 0
Solution:
Given equation is 9x² + 16y² = 144
\(\frac{x^{2}}{16}+\frac{y^{2}}{9}\) =1
∴ a = 4, b = 3
Length of major axis = 2a = 2. 4 = 8
Length of minor axis = 2b = 2. 3 = 6
Length of latus rectum = \(\frac{2b^{2}}{a}=\frac{2.9}{4}=\frac{9}{2}\)
Eccentricity = \(\sqrt{\frac{a^2-b^2}{a^2}}=\sqrt{\frac{16-9}{16}}=\frac{\sqrt{7}}{4}\)
Centre is C (0,0)
Foci are (± ae, 0) = (±√7, 0)
Equations of the directrices are x = ± \(\frac{a}{e}\)
x = ± 4.\(\frac{4}{\sqrt{7}}\) = ±\(\frac{16}{\sqrt{7}}\)
√7x = +16
(ii) Given equation is 4x² + y² – 8x + 2y + 1 =0
4(x² – 2x) + (y² + 2y) = -1
4(x – 1)² + (y + 1)² = 4 + 1 – 1 = 4
\(\frac{(x-1)^{2}}{2}+\frac{(y+1)^{2}}{2}\)= 1
Hence a < b ⇒ y – axis is major axis
a = 1, b = 2
Length of major axis = 2b = 4
Length of minor axis = 2a = 2
Length of latus rectum \(\frac{2a^{2}}{a}=\frac{2}{2}=1\)
Eccentricity = \(\sqrt{\frac{b^2-a^2}{b^2}}=\sqrt{\frac{4-1}{4}}=\frac{\sqrt{3}}{2}\)
Centre is C (-1, -1)
be = 2.\(\frac{\sqrt{3}}{2}\) = √3
Foci are (-1, 1 ±√3)
Equations of the directrices are y + 1 = ± \(\frac{b}{e}\)
= ± \(\frac{4}{\sqrt{3}}\)
√3y + √3 = ±4
√3y + √3 ± 4 = o
(iii) Given equation is x² + 2y² – 4x+ 12y + 14 = 0
x² – 4x + 2 (y² + 6y) = – 14
⇒ (x² – 4x + 4) + 2(y² + 6y + 9) = 4 + 18 – 14
⇒ (x – 2)² + 2(y + 3)² = 8
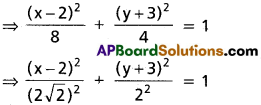
a = 2√2, b = 2, h = 2, k =-3
Length of major axis = 2a = 2(2 √2) = 4 √2
Length of minor axis = 2b = 2(2) = 4
Length of latus rectum
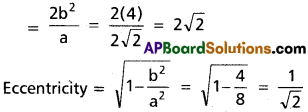
Centre = (h, k) = (2, – 3)
Foci = (h ± ae, k) = (2 ± 2, -3)
= (4, -3), (0, – 3)
Equations of the directrices are x- h = ± \(\frac{a}{e}\)
x – 2 = ±\(\frac{2 \sqrt{2}}{\left(\frac{1}{\sqrt{2}}\right)}\) x – 2 = ±4
i.e., x = 6, x = -2.
![]()
Question 2.
Find the equation of the ellipse in the form \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}\) = 1, given the following data.
i) Centre (2, -1), one end of major axis (2, – 5), e = \(\frac{1}{3}\).
Solution:
Centre (2, -1) ⇒ h = 2, k = -1
end of major axis (2, -5)
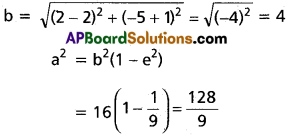
Equation of the ellipse is
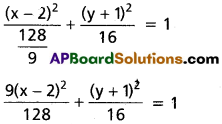
9(x – 2)² + 8(y + 1)² = 128
i.e., 9 (x – 2)² + 8 (y + 1)² = 128.
ii) Centre (4, -1), one end of major axis is (-1, -1) and passing through (8, 0).
Solution:
a = \(\sqrt{(4+1)^2+(-1+1)^2}\)
a = 5
passes through (8, 0)

Required equation be
\(\frac{(x-4)^2}{25}\) + \(\frac{9}{25}\)(y + 1)² = 1
⇒ (x – 4)² + 9(y + 1)² = 25
iii) Centre (0, -3), e = \(\frac{2}{3}\), semi-minor axis = 5.
Solution:
b = 5
⇒ b² = a² – a²e²
⇒ 25 = a² – a². \(\frac{4}{9}\) = a²\(\frac{5}{9}\)
⇒ 45 = a²
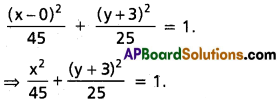
iv) Centre (2, -1); e = \(\frac{1}{2}\); length of latus rectum 4.
Solution:
Equation of the ellipse is
\(\frac{9(x-2)^2}{64}+\frac{3(y+1)^2}{16}\) = 1
9(x – 2)² + 12(y + 1)² = 64.
Question 3.
Find the radius of the circle passing through the foci of an ellipse 9x² + 16y² = 144 and having least radius.
Solution:
Equation of the ellipse 9x² + 16y² = 144.
\(\frac{x^2}{16}+\frac{y^2}{9}\) = 1
a² = 16, b² = 9
a = 4, b = 3
The circle passes through S and S¹ and has least radius.
If S S¹ is diameter.
a²e² = a² – a² (1 – e²) = a² – b² = 16 – 9 = 7
Equation of the required circle is x² + y² = 7.
![]()
Question 4.
A man running on a race course notices that the sum of the distances of the two flag posts from him is always 10m and the distance between the flag posts is 8m. Find the equation of the race course traced by the man.
Solution:
S and S¹ are the flags and P is the position of the man.
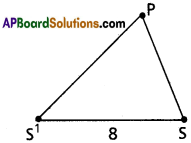
Given SP + S¹P = 10 and SS¹ = 8
The path traced by the man is an ellipse whose foci are S and S¹.
2a = 10 ⇒ a = 5
SS¹ = 8 ⇒ 2ae = 8 ⇒ ae = 4
b² = a² (1 – e²) = 25 (1 – \(\frac{16}{25}\)) = 9
Equation of the ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
\(\frac{x^2}{25}+\frac{y^2}{9}\) = 1.
III.
Question 1.
A line of fixed length (a + b) moves so that its ends are always on two perpendicular straight lines fixed. Prove that a marked point on the line, which divides this line into portions of lengths ‘a’ and ‘b’ describes an ellipse and also find the eccentricity of the ellipse when a = 8, b = 12.
Solution:
Take the perpendicular lines as co-ordinates axes. AB is the fixed line. Let OA = α, and OB = β so that equation of AB is \(\frac{x}{\alpha}+\frac{y}{\beta}\) = 1
Where α² + β² = (a + b)² ………….. (1)
P(x, y) divides AB in the ratio a = b
Co-ordinates of P are (\(\frac{b\alpha}{a+b}+\frac{a\beta}{a+b}\)) = (x, y)
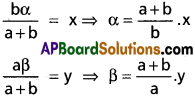
Substituing the values of α, β in (1) we get,
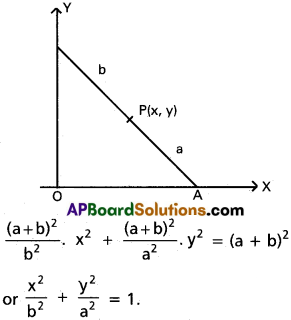
P describes an ellipse.
Given a = 8, b = 12, so that b > a
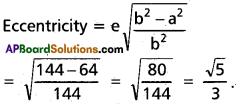
![]()
Question 2.
Prove that the equation of the chord joining the points α, β on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\)
![]()
Solution:
The given points on the ellipse are
P(a cos α, b sin α) and Q (a cos β, b sin β).

Equation of the chord PQ is
