Inter 2nd Year Maths 2B Ellipse Formulas

Use these Inter 2nd Year Maths 2B Formulas PDF Chapter 4 Ellipse to solve questions creatively.

Intermediate 2nd Year Maths 2B Ellipse Formulas

Definition:
→ A conic with eccentricity less than one is called an ellipse i.e., the locus of a point whose distances from a fixed point and a fixed straight line are in constant ratio ‘e’ which is less than 1, is called an ellipse. The fixed point and fixed straight line are called focus and directrix respectively.

Equation of Ellipse in standard form:
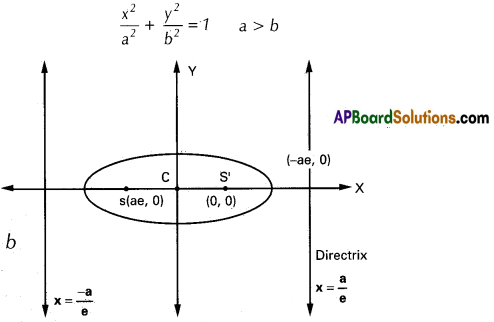
→ \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1; a > b, b² = a² (1 – e²) ; e < 1
Foci: (ae, 0), (- ae, 0); directrices x = \(\frac{\mathrm{a}}{\mathrm{e}}\); x = \(\frac{-a}{e}\)
a = Length of semi major axis.
b = Length of semi minor axis.

Various forms of the ellipse:

→ Major axis: along X – axis
Length of major axis: 2a
Minor axis: along Y-axis
Length of minor axis: 2b
Centre: (0, 0)
Foci: S (ae, 0); S’ (- ae, 0)
Directrices: x = \(\frac{\mathrm{a}}{\mathrm{e}}\); x = – \(\frac{\mathrm{a}}{\mathrm{e}}\)
e is given as: b² = a² (1 – e²)
(or) e = \(\sqrt{\frac{a^{2}-b^{2}}{a^{2}}}\), a > b
a < b (or) b > a

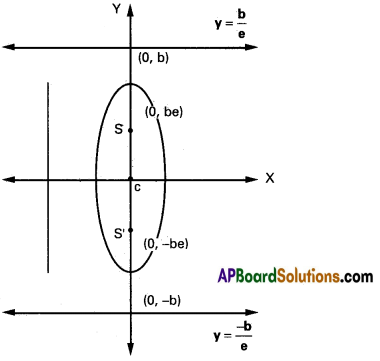
→ Major axis: along Y – axis
Length of major axis: 2b
Minor axis: along Y-axis
Length of minor axis: 2a
Centre: (0, 0)
Foci: S (0, be); S’ (0, – be)
Directrices: y = \(\frac{b}{\mathrm{e}}\), y = – \(\frac{b}{\mathrm{e}}\)
e is given as: a² = b² (1 – e²)
(or) e = \(\sqrt{\frac{b^{2}-a^{2}}{b^{2}}} .\)

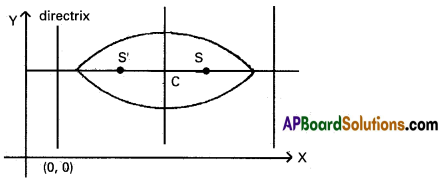
→ \(\frac{(x-\alpha)^{2}}{a^{2}}+\frac{(y-\beta)^{2}}{b^{2}}\) = 1, a > b
Major axis: parallel to X-axis along the line y = β
Length of major axis: 2a
Minor axis: parallel to Y-axis along the line x = α
Length of minor axis: 2b
Center: (α, β)
Foci: S (ae + α, β); S’ ( – ae + α, β)
Directrices: x = α + \(\frac{a}{e}\) ; x = α – \(\frac{a}{e}\)
e is given by b² = a² ( 1 – e²)

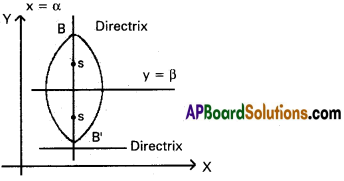
→ \(\frac{(x-\alpha)^{2}}{a^{2}}+\frac{(y-\beta)^{2}}{b^{2}}\) = 1, a < b
Major axis: parallel to Y-axis along the line x = α
Length of major axis: 2b
Minor axis: parallel to X-axis along the line y = β
Length of minor axis: 2a
Center: (α, β)
Foci: S (α, be + β); S’ (α, -be + β)
Directrices: y – β = \(\frac{b}{\mathrm{e}}\) ; y – β = – \(\frac{b}{\mathrm{e}}\)

→ A line segment joining two points on the ellipse is called a chord of the ellipse. Chord passing through foci is called a focal chord. A focal chord perpendicular to the major axis of the ellipse is cal fed latus rectum. Length of latus rectum = \(\frac{2 b^{2}}{a}\), a > b, Length of the latus rectum = \(\frac{2 a^{2}}{a}\), if b > a

→ If P (x, y) is any point on the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 whose foci are S and S’.
Then SP + SP’ = constant = 2a.

→ Parametric equations x = a cos θ; y = b sin θ

→ If P a point lies outside the ellipse, then S₁₁ > 0.

→ If P a point lies on the ellipse, then S₁₁ = 0.

→ If P a point lies inside the ellipse, then S₁₁ < 0.

Ellipse:
A conic is said to be an ellipse if it’s eccentricity e is less than 1.

Equation of an Ellipse in Standard Form:
The equation of an ellipse in the standard form is \(\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}\) = 1.(a < b)
Proof:

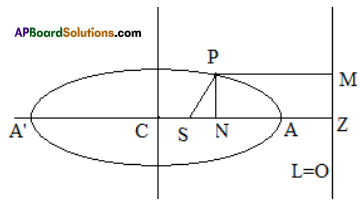
Let S be the focus, e be the eccentricity and L = 0 be the directrix of the ellipse. Let P be a point on the ellipse. Let M, Z be the projections (foot of the perpendiculars) of P, S on the directrix L = 0 respectively. Let N be the projection of P on SZ. Since e < 1, we can divide SZ both internally and externally in the ratio e: 1. Let A, A’ be the points of division of SZ in the ratio e: 1 internally and externally respectively. Let AA’ = 2a. Let C be the midpoint of AA’. The points A, A’ lie on the ellipse and
\(\frac{S A}{A Z}\) = eAZ, \(\frac{\mathrm{SA}^{\prime}}{\mathrm{A}^{\prime} \mathrm{Z}}\) = eA’Z
Now SA + SA’ = eAZ + eA’Z
⇒ AA’ = e(AZ + A’Z)
⇒ 2a = e(CZ – CA + A’C + CZ)
⇒ 2a = e.2CZ (∵ CA = A’C)
⇒ CZ = a/e

Also SA’- SA = eA’Z – eAZ
⇒ A’C + CS – (CA – CS) = e(A’Z – AZ)
⇒ 2CS = eAA’ (∵ CA = A’C)
⇒ 2CS = e2a ⇒ CS = ae
Now PM = NZ = CZ – CN = \(\frac{a}{e}\) – x₁

P lies on the ellipse:
⇒ \(\frac{\mathrm{PS}}{\mathrm{PM}}\) = e ⇒ PS = ePM ⇒ PS² = e²PM²
⇒ (x₁ – ae)² + (y₁ – 0)² = e²\(\left(\frac{\mathrm{a}}{\mathrm{e}}-\mathrm{x}_{1}\right)^{2}\)
⇒ (x₁ – ae)² + y₁² = (a – x₁e)²
⇒ x₁ + ae – 2x₁ae + y₁ = a + x₁e – 2x₁ae
⇒ (1 – e²)x₁² + y₁² = (1 – e²)a²
⇒ \(\frac{x_{1}^{2}}{a^{2}}+\frac{y_{1}^{2}}{a^{2}\left(1-e^{2}\right)}\) = 1 ⇒ \(\frac{x_{1}^{2}}{a^{2}}+\frac{y_{1}^{2}}{b^{2}}\) = 1
Where b² = a²(1 – e²) > 0
The locus of P is \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1.
∴ The equation of the ellipse is \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1.
Nature of the Curve \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1.

Let be the curve represented by \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1. Then

• The curve is symmetric about the coordinate axes.
• The curve is symmetric about the origin O and hence O is the midpoint of every chord of the ellipse through O. Therefore the origin is the centre of the ellipse.
• Put y = 0 in the equation of the ellipse ⇒ x = a ⇒ x = ±a.
  Thus the curve meets x-axis (Principal axis) at two points A(a, 0), A'(-a, 0). Hence the ellipse has two vertices. The axis AA’ is called major axis. The length of the major axis is AA’ = 2a
• Put x = 0 ⇒ y² = b² ⇒ y = ± b. Thus, the curve meets y-axis (another axis) at two points B(0, b), B'(0, -b). The axis BB’ is called minor axis and the length of the minor axis is BB’ = 2b.
• The focus of the ellipse is S(ae, 0). The image of S with respect to the minor axis is S'(-ae,0). The point S’ is called second focus of the ellipse.
• The directrix of the ellipse is x = a/e. The image of x = a/e with respect to the minor axis is x = -a/e. The line x = -a/e is called second directrix of the ellipse.
• \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
  y² = b²(1 – \(\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}\)) ⇒ y = \(\frac{b}{a} \sqrt{a^{2}-x^{2}}\)

Thus y has real values only when -a ≤ x ≤ a. Similarly x has real values only when -b ≤ y ≤ b. Thus the curve lies completely with in the rectangle x = ±a, y = ±b. Therefore the ellipse is a closed curve.

Theorem:
The length of the latus rectum of the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 (a > b > 0) is \(\frac{2 b^{2}}{a}\)
The length of the latus rectum of the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 (0 < a < b) is \(\frac{2 b^{2}}{a}\)

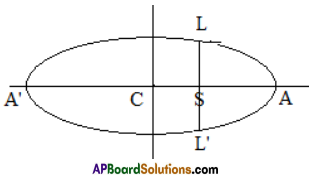
Let LL’ be the length of the latus rectum of the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1.
Focus S = (ae, 0)
If SL = 1, then L = (ae, 1)
L is lies on the ellipse ⇒ \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
⇒ e + \(\frac{1^{2}}{\mathrm{~b}^{2}}\) = 1 ⇒ \(\frac{1^{2}}{\mathrm{~b}^{2}}\) = 1 – e = \(\frac{\mathrm{b}^{2}}{\mathrm{a}^{2}}\) ⇒ 1 = \(\frac{b^{4}}{a^{2}}\)
⇒ 1 = \(\frac{b^{2}}{a}\) ⇒ SL = \(\frac{b^{2}}{a}\)
LL’ = 2SL = \(\frac{2 b^{2}}{a}\)

Note: The coordinates of the four ends of the latus recta of the ellipse \(\frac{\mathrm{b}^{2}}{\mathrm{a}}\) = 1 (a < b < 0) are L = (ae, \(\frac{\mathrm{b}^{2}}{\mathrm{a}}\)), L’ = (ae, –\(\frac{\mathrm{b}^{2}}{\mathrm{a}}\)), L₁ = (-ae, \(\frac{\mathrm{b}^{2}}{\mathrm{a}}\)); L₁‘ = (-ae, \(\frac{\mathrm{b}^{2}}{\mathrm{a}}\))

Note: The coordinates of the four ends of the latus recta of the ellipse \(\frac{\mathrm{b}^{2}}{\mathrm{a}}\) = 1 (0 < a < b) are L = (\(\frac{\mathrm{a}^{2}}{\mathrm{~b}}\), be), L’ = (-\(\frac{\mathrm{a}^{2}}{\mathrm{~b}}\), be), L₁ = (\(\frac{\mathrm{a}^{2}}{\mathrm{~b}}\), -be), L₁‘ = (\(\frac{\mathrm{a}^{2}}{\mathrm{~b}}\), -be)

Theorem:
If P is a point on the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 with foci S and S then PS + PS’ = 2a.
Proof:
Let e be the eccentricity and L = 0, L’ = 0 be the directrices of the ellipse.
Let C be the centre and A, A’ be the vertices of the ellipse.
∴ AA’ = 2a
Foci of the ellipse are S(ae, 0), S'(-ae, 0)
Let P(x₁, y₁) be a point on the ellipse

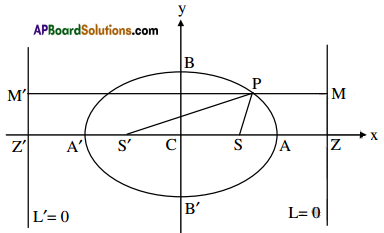
Let M, M’ be the projections of P on the directrices L = 0, L’ = 0 respectively.
∴ \(\frac{\mathrm{SP}}{\mathrm{PM}}\) = e, \(\frac{\mathrm{S}^{\prime} \mathrm{P}}{\mathrm{PM}^{\prime}}\) = e

Let Z, Z’ be the points of intersection of major axis with directrices.
∴ MM’ = ZZ’ = CZ + CZ’ = 2a/e.
PS + PS’ = ePM + ePM’
= e(PM + PM’) = e(MM’) = e(2a/e) = 2a.

Theorem:
Let P(x₁, y₁) be a point and S ≡ \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) – 1 = 0 be an ellipse. Then
(i) P lies on the ellipse ⇔ S₁₁ = 0,
(ii) P lies inside the ellipse ⇔ S₁₁ < 0,
(iii) P lies outside the ellipse ⇔ S₁₁ > 0

Theorem:
The equation of the tangent to the ellipse S = 0 at F(x₁, y₁) is S₁ = 0.

Theorem:
The equation of the normal to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 F(x₁, y₁) is \(\frac{a^{2} x}{x_{1}}-\frac{b^{2} y}{y_{1}}\) = a² – b².
Proof:
The equation of the tangent to S = 0 at F is S₁ = 0
⇒ \(\frac{\mathrm{xx}_{1}}{\mathrm{a}^{2}}+\frac{\mathrm{yy}_{1}}{\mathrm{~b}^{2}}\) – 1 =
The equation of the normal to S = 0 at F is
\(\frac{\mathrm{y}_{1}}{\mathrm{~b}^{2}}\)(x – x₁) – \(\frac{\mathrm{x}_{1}}{\mathrm{~a}^{2}}\)(y – y₁) = 0
⇒ \(\frac{x_{1}}{b^{2}}-\frac{y_{1}}{a^{2}}=\frac{x_{1} y_{1}}{b^{2}}-\frac{x_{1} y_{1}}{a^{2}}\)
⇒ \(\frac{\mathrm{a}^{2} \mathrm{~b}^{2}}{\mathrm{x}_{1} \mathrm{y}_{1}}\left(\frac{\mathrm{xy}}{\mathrm{b}^{2}}-\frac{\mathrm{y} \mathrm{x}_{1}}{\mathrm{a}^{2}}\right)=\frac{\mathrm{a}^{2} \mathrm{~b}^{2}}{\mathrm{x}_{1} \mathrm{y}_{1}}\left(\frac{\mathrm{x}_{1} \mathrm{y}_{1}}{\mathrm{~b}^{2}}-\frac{\mathrm{x}_{1} \mathrm{y}_{1}}{\mathrm{a}^{2}}\right)\)
⇒ \(\frac{a^{2} x}{x_{1}}-\frac{b^{2} y}{y_{1}}\) = a² – b²

Theorem:
The condition that the line y = mx + c may be a tangent to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) – 1 is c² = a²m² + b².
Proof:
Suppose y = mx + c … (1)is a tangent to the e11ipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1.
Let P(x1, y) be the point of contact.
The equation of the tangent at P is
\(\frac{\mathrm{xx}_{1}}{\mathrm{a}^{2}}+\frac{\mathrm{yy}_{1}}{\mathrm{~b}^{2}}\) – 1 = 0 … (2)

Now (1) and (2) represent the same line.
\(\frac{\mathrm{x}_{1}}{\mathrm{a}^{2} \mathrm{~m}}=\frac{\mathrm{y}_{1}}{\mathrm{~b}^{2}(-1)}=\frac{-1}{\mathrm{c}}\) ⇒ x₁ = \(\frac{-a^{2} m}{c}\), y₁ = \(\frac{\mathrm{b}^{2}}{\mathrm{c}}\)
P lies on the line y = mx + c ⇒ y₁ = mx₁ + c
⇒ \(\frac{\mathrm{b}^{2}}{\mathrm{c}}\) = m\(\left(\frac{-a^{2} m}{c}\right)\) + c ⇒ b² = -a²m² + c²
⇒ c² = a²m² + b²

Note:
The equation of a tangent to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 may be taken as y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\). The point of contact is \(\left(\frac{-\mathrm{a}^{2} \mathrm{~m}}{\mathrm{c}}, \frac{\mathrm{b}^{2}}{\mathrm{c}}\right)\) where c² = a²m² + b²

Theorem:
Two tangents can be drawn to an ellipse from an external point.

Director Circle:
The points of intersection of perpendicular tangents to an ellipse S = 0 lies on a circle, concentric with the ellipse.
Proof:
Equation of the ellipse
S ≡\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 0
Let P(x₁, y₁) be the point of intersection of perpendicular tangents drawn to ellipse.

Let y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\) be a tangent to the ellipse S = 0 passing through P.
y₁ = mx₁ ± \(\sqrt{a^{2} m^{2}+b^{2}}\)
⇒ y₁ – mx₁ = ± \(\sqrt{a^{2} m^{2}+b^{2}}\)
⇒ (y₁ – mx₁)² = a²m² + b²
⇒ y₁² + m²x₁² – 2x₁y₁m = a²m² + b²
⇒ (x₁² – a²)m² -2x₁y₁m + (y₁² -b²) = 0 … (1)

If m₁, m₂ are the slopes of the tangents through P then m1, m2 are the roots of (1).
The tangents through P are perpendicular.
⇒ m₁m₂ = -1 ⇒ \(\frac{y_{1}^{2}-b^{2}}{x_{1}^{2}-a^{2}}\) = -1
⇒ y₁² – b² = -x² + a² ⇒ x²₁ + y²₁ = a² + b²
∴ P lies on x² + y² = a² + b² which is a circle with centre as origin, the centre of the ellipse.

Auxiliary Circle:
Theorem: The feet of the perpendiculars drawn from either of the foci to any tangent to the ellipse S = 0 lies on a circle, concentric with the ellipse.( called auxiliary circle)
Proof:
Equation of the ellipse S ≡ \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) – 1 = 0
Let P(x₁, y₁) be the foot of the perpendicular drawn from either of the foci to a tangent.
The equation of the tangent to the ellipse S = 0 is y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\) … (1)
The equation to the perpendicular from either foci (±ae, 0) on this tangent is
y = –\(\frac{1}{m}\)(x ± ae)

Now P is the point of intersection of (1) and (2)

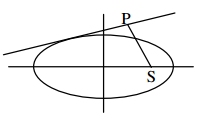
∴ y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\), y₁ = –\(\frac{1}{m}\)(x₁ ± ae
⇒ y₁ – mx₁ = ±V a2m2 + b2, my₁ + x₁ = ±ae
⇒ (y₁ – mx₁)² + (my₁ + x₁)² = a²m² + b² + a²e²
⇒ y₁² + m²x² – 2x₁y₁m + m²y₁² + x₁² + 2x₁y₁m = a²m² + a²(1 – e²) + a²e²
⇒ x₁²(m² + 1) + y₁²(1 + m²) = a²m² + a²
⇒ (x₁² + y₁²)(m² + 1) = a² (m² + 1)
⇒ x₁² + y₁² = a²
P lies on x² + y² = a² which is a circle with centre as origin, the centre of the ellipse.

Theorem:
The equation to the chord of contact of P(x₁, y₁) with respect to the ellipse S = 0 is S₁ = 0.

Eccentric Angle Definition:
Let P(x, y) be a point on the ellipse with centre C. Let N be the foot of the perpendicular of P on the major axis. Let NP meets the auxiliary circle at P’. Then ∠NCP’ is called eccentric angle of P. The point P’ is called the corresponding point of P.

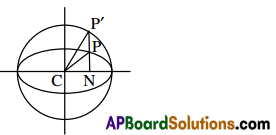
Parametric Equations: If P(x, y) is a point on the ellipse then x = a cos θ, y = b sin θ where θ is the eccentric angle of P. These equations x = a cos θ, y = b sin θ are called parametric equations of the ellipse. The point P(a cos θ, b sin θ) is simply denoted by θ.

Theorem: The equation of the chord joining the points with eccentric angles α and β on the ellipse S = 0 is \(\frac{x}{a} \cos \frac{\alpha+\beta}{2}+\frac{y}{b} \sin \frac{\alpha+\beta}{2}=\cos \frac{\alpha-\beta}{2}\)
Proof:
Given points on the ellipse are P(a cos α, b sin α), Q(a cos β, b sin β).
Slope of \(\overline{\mathrm{PQ}}\) is \(\frac{\mathrm{b} \sin \alpha-\mathrm{b} \sin \beta}{\mathrm{a} \cos \alpha-\mathrm{a} \cos \beta}=\frac{\mathrm{b}(\sin \alpha-\sin \beta)}{\mathrm{a}(\cos \alpha-\cos \beta)}\)
Equation of \(\overline{\mathrm{PQ}}\) is:

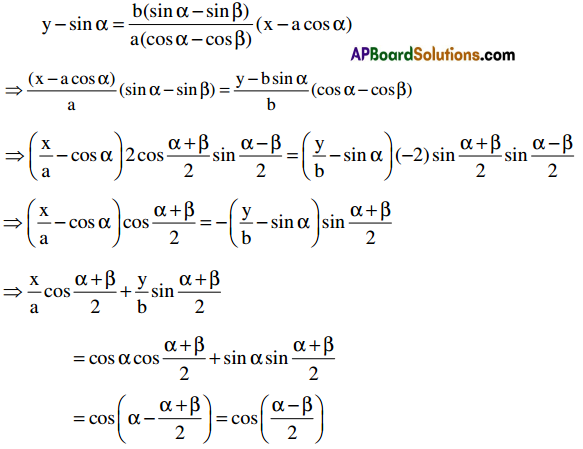
Theorem: The equation of the tangent at P(θ) on the ellipse
S = 0 is \(\frac{x}{a}\) cos θ + \(\frac{y}{b}\) sin θ = 1.

Theorem: The Equation of The Normal At P(θ) On The Ellipse
S = 0 Is \(\frac{a x}{\cos \theta}-\frac{b y}{\sin \theta}\) = a² – b².

Theorem: Four normals can be drawn from any point to the ellipse and the sum of the eccentric angles of their feet is an odd multiple of π.