Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Differential Equations Solutions Exercise 8(b) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2B Differential Equations Solutions Exercise 8(b)
I.
Question 1.
Find the general solution of \(\sqrt{1-x^2}\) dy + \(\sqrt{1-y^2}\) dx = 0.
Solution:
Given differential equation is
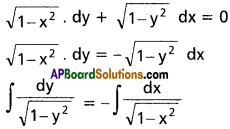
sin-1 y = – sin-1 x + c
Solution is sin-1 x + sin-1 y = c, where c is a constant.
Question 2.
Find the general solution of \(\frac{dy}{dx}=\frac{2y}{x}\).
Solution:
\(\frac{dy}{dx}=\frac{2y}{x}\)
∫\(\frac{dy}{dx}\) = 2∫\(\frac{2y}{x}\)
log c + log y = 2 log x
log cy = log x²
Solution is cy = x², where c. is a constant.
II. Solve the following differential equations.
Question 1.
\(\frac{dy}{dx}=\frac{1+y^2}{1+x^2}\)
Solution:
\(\frac{dy}{dx}=\frac{1+y^2}{1+x^2}\)
∫\(\frac{dy}{1+y^2}\) = ∫\(\frac{dx}{1+x^2}\)
tan-1 y = tan-1 x + tan-1c where c is a constant.
![]()
Question 2.
\(\frac{dy}{dx}\) = ey-k
Solution:
\(\frac{dy}{dx}=\frac{e^y}{e^x}\)
\(\frac{dy}{e^y}=\frac{dx}{e^x}\)
∫e-xdx = ∫e-ydy
-e-x = -e-y + C
e-y = e-x + c where c is a constant.
Question 3.
(ex + 1) y dy + (y + 1) dx = 0
Solution:
(ex + 1 )y. dy = – (y + 1) dx
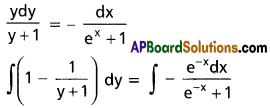
y – log (y + 1) = log (e-x + 1) + log c
⇒ y – log (y + 1) = log c (e-x + 1)
⇒ y = log (y + 1) + log c (e-x + 1)
y = log c (y + 1) (e-x +1)
Solution is
ey = c(y + 1) (e-x +1)
Question 4.
\(\frac{dy}{dx}\) = ex-y + x²e-y
Solution:
\(\frac{dy}{dx}\) = ex-y + x² . e-y
= \(\frac{e^x}{e^y}=\frac{x^2}{e^y}\)
∫ey . dy = ∫(ex + x²) dx
Solution is
ey = ex + \(\frac{x^3}{3}\) + c
Question 5.
tan y dx + tan x dy = 0
Solution:
tan y dx = – tan x dy
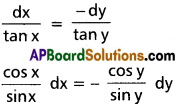
log sin x = – log sin y + log c
log sin x + log sin y = log c
log (sin x . sin y) = log c
⇒ sin x . sin y = c is the solution
![]()
Question 6.
\(\sqrt{1+x^2}\)dx + \(\sqrt{1+y^2}\)dy = 0
Solution:
\(\sqrt{1+x^2}\)dx = –\(\sqrt{1+y^2}\)dy
Integrating both sides we get
∫\(\sqrt{1+x^2}\)dx = -∫\(\sqrt{1+y^2}\)dy
Integrating both sides we get
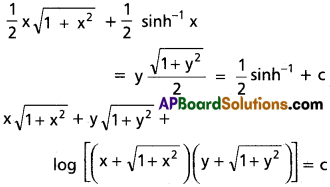
Question 7.
y – x\(\frac{dy}{dx}\) = 5(y² + \(\frac{dy}{dx}\))
Solution:
y – 5y² = (x + 5)\(\frac{dy}{dx}\)
\(\frac{dx}{x+5}=\frac{dy}{y(1-5y}\)
Integrating both sides
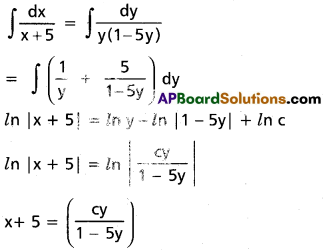
Question 8.
\(\frac{dy}{dx}=\frac{xy+y}{xy+x}\)
Solution:
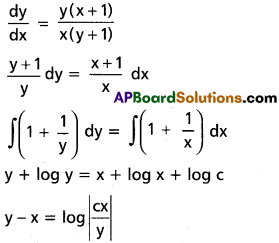
III. Solve the following differential equations.
Question 1.
\(\frac{dy}{dx}=\frac{1+y^2}{(1+x^2)xy}\)
Solution:

log (1 + y²) = log x² – log (1 + x²) + log c
log (1 + x²) + log (1 + y²) = log x² + log c
Solution is (1 + x²) (1 + y²) = cx²
Question 2.
\(\frac{dy}{dx}\) + x² = x² e3y
Solution:

log(1 – e-3y) = x³ + c'(c’ = 3c)
Solution is
1 – e-3y = ex³ . k(k = ec’)
Question 3.
(xy² + x)dx+(yx²+y)dy = 0.
Solution:
(xy² + x) dx + (yx² + y) dy = 0
x(y² + 1) dx + y (x² + 1) dy = 0
Dividing with (1 + x²) (1 + y²)
\(\frac{x dx}{1+x^2}+\frac{y dy}{1+y^2}\) = 0
Integrating
∫\(\frac{x dx}{1+x^2}\) + ∫\(\frac{y dy}{1+y^2}\) = 0
\(\frac{1}{2}\) [(log (1 + x²) + log (1 + y²)] = log c
log (1 + x²) (1 + y²) = 2 log c = log c²
Solution is (1 + x²) (1 + y²) = k when k = c².
![]()
Question 4.
\(\frac{dy}{dx}\) = 2y tanh x
Solution:
\(\frac{dy}{dx}\) = 2y tanh x
\(\frac{dy}{y}\) = 2 tanh x dx
Integrating both sides we get
∫\(\frac{dy}{y}\) = 2 ∫ tanh x dx
log y = 2 log |cosh x| + log c
lny = 2ln cosh x + In c
y = c cos²h x
Question 5.
sin-1 \(\frac{dy}{dx}\) = x + y
Solution:
\(\frac{dy}{dx}\) = sin(x + y)
x + y = t
1 + \(\frac{dy}{dx}=\frac{dt}{dx}\)
\(\frac{dt}{dx}\) – 1 = sin t
\(\frac{dt}{dx}\) = 1 + sin t
Integrating both sides we get
∫\(\frac{dt}{1+\sin t}\) = ∫dx
∫\(\frac{1-\sin t}{\cos^2 t}\) dt = x + c
∫sec² t dt – ∫tan t . sec t dt = x + c
tan t – sec t = x + c
⇒ tan (x + y) – sec (x + y) = x + c
Question 6.
\(\frac{dy}{dx}+\frac{y^2+y+1}{x^2+x+1}\) = 0
Solution:
\(\frac{-dy}{y^2+y+1}=\frac{dx}{x^2+x+1}\)
Integrating both sides dy
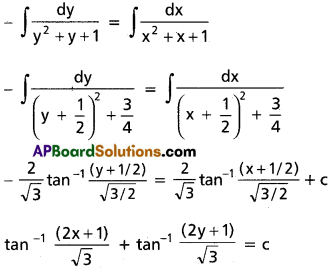
![]()
Question 7.
\(\frac{dy}{dx}\) = tan² (x + y)
Solution:
\(\frac{dy}{dx}\) = tan² (x + y)
put v = x + y

2v + sin 2v = 4x + c’
2(x + y) + sin 2(x + y) = 4x + c’
x – y – \(\frac{1}{2}\)sin [2(x + y)] = c