Inter 2nd Year Maths 2A Theory of Equations Important Questions

Students get through Maths 2A Important Questions Inter 2nd Year Maths 2A Theory of Equations Important Questions which are most likely to be asked in the exam.

Intermediate 2nd Year Maths 2A Theory of Equations Important Questions

Question 1.
Form polynomial equation of the lowest degree, with roots 1, -1, 3 (May ’06)
Hint : Equation having roots, α, β, γ is [(x – α)(x – β)(x – γ) = 0
Solution:
Required equation is
(x – 1) (x + 1) (x – 3) = 0
⇒ (x² – 1) (x – 3) = 0
⇒ -3x² – x + 3 = 0

Question 2.
If 1, 1 α are the roots of
x³ – 6x² + 9x – 4 = 0, then find α. (May ’11)
Solution:
1, 1, α are roots of x³ – 6x² + 9x – 4 = 0
Sum = 1 + 1 + α = 6
α = 6 – 2 = 4

Question 3.
If -1, 2 and α are the roots of 2x³ + x² – 7x – 6 = 0, then find α (Mar 14, 13)
Solution:
-1, 2, α are roots of 2x³ + x² – 7x – 6 = 0
sum = -1 + 2 + α = –\(\frac{1}{2}\)
α = –\(\frac{1}{2}\) – 1 = –\(\frac{3}{2}\)

Question 4.
If 1, -2 and 3 are roots of x³ – 2x² + ax + 6 = 0, then find α. (Mar. ’04,)
Solution:
1, -2 and 3 are roots of x³ + x² + ax – 6 = 0
x³ – 2x + ax + 6 = 0
⇒ 1(-2) + (-2) 3 + 3. 1 = a
i.e., a = -2 – 6 + 3 = -5

Question 5.
If the product of the roots of 4x³ + 16x² – 9x – a = 0 is 9, then find a. (TS Mar. ’17, ’16)
Solution:
α, β, γ are the roots of
4x³ + 16x² – 9x – a = 0
αβγ = \(\frac{a}{4}\) = 9 ⇒ a = 36

Question 6.
Find the transformed equation whose roots are the negative of the roots of
x⁴ + 5x³ + 11x + 3 = 0
Solution:
Given f(x) = x⁴ + 5x³ + 11x + 3 = 0
We want an equation whose roots are
-α₁, α₂, α₃, α₄,
Required equation f(-x) = 0
⇒ (-x)⁴ + 5 (-x)³ + 11 (-x) + 3 = 0
⇒ x⁴ – 5x³ – 11x + 3 = 0

Question 7.
Form the polynomial equation of degree 3 whose roots are 2, 3 and, 6.
Solution:
The required polynomial equation is,
(x – 2) (x – 3) (x – 6) = 0
⇒ x³ – 11x² + 36x – 36 = 0

Question 8.
Let α, β, γ be the roots of Σα³
Solution:
Σα³ = α³ + β³ + γ³
= (α + β + γ)
= (α² + β² + γ² – αβ – βγ – γα) + 3αβγ
= (-p)(p² – 2q – q) – 3r
= -p(p² – 3q) – 3r
∴ Σα³ = -p³ + 3pq – 3r = 3pq – p³ – 3r

Question 9.
If α, β and 1 are the roots of x³ – 2x² – 5x + 6 = 0, then find α and β (AP Mår ’16, ’08)
Solution:
α, β and 1 are the roots of
x³ – 2x² – 5x + 6 = 0
Sum = α + β + 1 = 2 ⇒ α + β = 1
product = αβ = -6
(α – β)² = (α + β )² – 4αβ = 1 + 24 = 25
α – β = 5
α + β = 1
Adding 2α = 6 ⇒ α = 3
∴ α = 3 and β = -2

Question 10.
If α, β and γ are the roots of x³ – 2x² + 3x – 4 = 0, then find
i) Σα²β²
ii) Σαβ (α + β)
Solution:
Since α, β, γ are the roots of
x³ – 2x² + 3x – 4 = 0
then α + β + γ = 2
αβ + βγ + γα = 3
αβγ = 4

i) Σα²β² = α²β² + β²γ² + γ²α²
= (αβ + βγ + γα)² – 2αβγ(α + β + γ)
= 9 – 2. 2.4 = 9 – 16 = -7

ii) Σαβ (α + β) = α²β + β²γ + γ²α + αβ² + βγ² + γα²
= (αβ + βγ + γα)(α + β + γ) – 3αβγ
= 2.3 – 3.4 = 6 – 12 = -6.

Question 11.
Solve the x³ – 3x² – 6x + 8 = 0 equation, given that the roots of each are in A.P. (‘Mar. ’07)
Solution:
The roots of x³ – 3x² – 6x + 8 = 0 are in A.P
Suppose a – d, a, a + d be the roots
Sum = a – d + a + a + d = 3
3a = 3
⇒ a = 1
∴ (x – 1) is a factor of x³ – 3x² – 6x + 8 = 0

⇒ x² – 2x – 8 = 0
⇒ x² – 4x + 2x – 8 = 0
⇒ x(x – 4) + 2(x – 4) = 0
⇒ x = 4, -2
∴ The roots are -2, 1, 4.

Question 12.
Solve x⁴ – 4x² + 8x + 35 = 0, given that 2 + i \(\sqrt{3}\) is a root (AP Mar. ’15)
Solution:
Let 2 + i \(\sqrt{3}\) is one root
⇒ 2 – i \(\sqrt{3}\) is another root.
The equation having roots
2 ± i \(\sqrt{3}\) is x² – 4x + 7 = 0
∴ x² – 4x + 7 is a factor of

∴ The roots of the given equation are 2 ± i\(\sqrt{3}\), -2 ± i

Question 13.
Find the polynomial equation whose roots are the reciprocals of the roots of x⁴ – 3x³ + 7x² + 5x – 2 = 0 (TS Mar. ’15, ’11)
Solution:
Given equation is
f(x) = x⁴ – 3x³ + 7x² + 5x – 2 = 0
Required equation is f(\(\frac{1}{x}\)) = 0
i.e. \(\frac{1}{x^{4}}\) – \(\frac{3}{x^{3}}\) + \(\frac{7}{x^{2}}\) + \(\frac{5}{x}\) – 2 = 0
Multiplying with x⁴
⇒ 1 – 3x + 7x² + 5x³ – 2x⁴ = 0
i.e., 2x⁴ – 5x³ – 7x² + 3x – 1 = 0

Question 14.
Find the polynomial equation whose roots are the translates of those of x⁵ – 4x⁴ + 3x² – 4x + 6 = 0 by -3. (TS Mar. 16)
Solution:
Given equation is
f(x) = x⁵ – 4x⁴ + 3x² – 4x + 6 = 0
Required equation is f(x + 3) = 0
(x + 3)⁵ – 4(x + 3)⁴ + 3(x + 3)²

Required equation is
x⁵ + 11x⁴ + 42x³ + 57x² – 13x – 60 = 0

Question 15.
Show that x⁵ – 5x³ + 5x² – 1 = 0 has three equal roots and find this root. (TS Mar. ’17)
Solution:
Let f(x) = x⁵ – 5x³ + 5x² – 1
f'(x) = 5x⁴ – 15x² + 10x
= 5x (x³ – 3x + 2)
f'(1) = 5(1) (1 – 3 + 2) = 0
f(1) = 1 – 5 + 5 – 1 = 0
x – 1 is a factor of f'(x) and f(x)
∴ 1 is a repeated’ root of f(x).

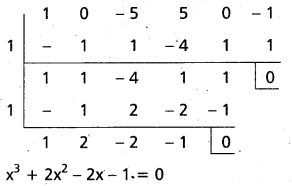
⇒ 1 is a root of above equation
(∵ sum of the coefficients is zero)
∴ 1 is the required root.

Question 16.
Solve the 8x³ – 36x² – 18x + 81 = 0 equation, given that the roots of each are in AP. (Mar. 04’)
Soluution:
Given the roots of 8x³ – 36x² – 18x + 81 = 0 are in AP.
Let the roots be a – d, a, a + d
Sum of the roots = a – d + a + a + d
= \(\frac{36}{8}\) = \(\frac{9}{2}\)
i.e., 3a = \(\frac{9}{2}\) ⇒ a = \(\frac{3}{2}\)
∴ (x – \(\frac{3}{2}\)) is a factor of

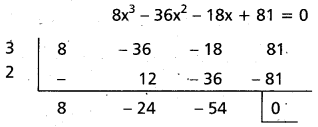
⇒ 8x² – 24x – 54 = 0
⇒ 4x² – 12x – 27 = 0
⇒ 4x² – 18x + 6x – 27 = 0
⇒ 2x(2x – 9) + 3 (2x – 9) = 0
⇒ (2x + 3) (2x – 9) = 0
⇒ x = –\(\frac{3}{2}\), \(\frac{9}{2}\)
The roots are –\(\frac{3}{2}\), \(\frac{3}{2}\), \(\frac{9}{2}\)

Question 17.
Solve the 3x³ – 26x² + 52x – 24 = 0 equations, given that the roots of each are in GP.
(TS Mar. ’15)
Solution:
Given equation is 3x³ – 26x² + 52x – 24 = 0
The roots are in G.P.
Suppose \(\frac{a}{r}\), a, ar are the roots.
Product = \(\frac{a}{r}\).a.ar = –\(\left(-\frac{24}{3}\right)\)
a³ = 8 ⇒ a = 2
∴ (x – 2) is a factor of 3x³ – 26x² + 52x – 24

⇒ 3x³ – 20x + 12 = 0
⇒ 3x² – 18x – 2x + 12 = 0
⇒ 3x (x – 6) -2 (x – 6) = 0
⇒ (3x – 2)(x – 6) = 0
⇒ x = \(\frac{2}{3}\), 6
∴ The roots are \(\frac{2}{3}\), 2, 6.

Question 18.
Solve 18x³ + 81x² + 121x + 60 = 0 given that one root is equal to half the sum of the
remaining roots. (May ’11; Mar. ’05)
Solution:
Suppose α, β, γ are the roots of 18x³ + 81x² + 121x + 60 = 0.

Question 19.
Solve the equation
2x⁵ + x⁴ – 12x³ – 12x² + x + 2 = 0 (AP Mar.17, 16; Mar. ‘08, 07)
Solution:
Given f(x) = 2x⁵ + x⁴ – 12x³ – 12x² + x + 2 = 0
This is an odd degree reciprocal equation of first type.
∴ -1 is a root.
Dividing f(x) with x + 1

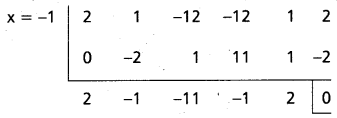
Dividing f(x) by (x + 1) we get
2x⁴ – x³ – 11x² – x + 2 = 0
Dividing by x²

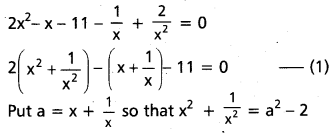
Substituting in (1), required equation is
2(a² – 2) – a – 11 = 0 .
2a² – 4 – a – 11 = 0
2a² – a – 15 = 0
(a – 3)(2a + 5) = 0
a = 3 or \(-\frac{5}{2}\)
Case (i) a = 3

Question 20.
Find the roots of
x⁴ – 16x³ + 86x² – 176x + 105 = 0
Solution:
Let f(x) = x⁴ – 16x³ + 86x² – 176x + 105
Now, f(1) = 1 – 16 + 86 – 176 + 105 = 0
∴ 1 is a root of f(x) = 0
⇒ x – 1 is a factor of f(x)

∴ f(x) = (x – 1) (x³ – 15x² + 71x – 105)
= (x – 1) g(x) where
g(x) = x³ – 15x² + 71x – 105
g(1) = 1 – 15 + 71 – 105 = -48 ≠ 0
g(2) = -15 ≠ 0
g(3) = 27 – 135 + 213 – 105 = 0
∴ 3 is a root of g(x) =0
⇒ x – 3 is a factor of g(x)

∴ g(x) = (x – 3) (x² – 12x + 35)
= (x – 3) (x – 5) (x – 7)
∴ f(x) = (x – 1) (x – 3) (x – 5) (x – 7)
∴ 1, 3, 5, 7 are the roots of f(x) = 0.

Question 21.
Solve 4x³ – 24x² + 23x + 18 = 0, given that the roots of this equation are in arithmetic progression (Mar. ’14; May ’06)
Solution:
Let a – d, a, a + d are the roots of the given equation
Now, sum of the roots
a – d + a + a + d = \(\frac{24}{4}\)
3a = 6
a = 2
Product of the roots (a – d) a (a + d) = \(-\frac{18}{4}\)
a(a² – d) = \(-\frac{9}{2}\)
2(4 – d²) = \(-\frac{9}{2}\)
4(4 – d²) = -9
16 – 4d² = -9
4d² = 25
d = ±\(\frac{5}{2}\)
∴ roots are –\(\frac{1}{2}\), 2 and \(\frac{9}{2}\)

Question 22.
Find the polynomial equation whose roots are the squares of the roots of x⁵ + 4x³ – x² + 11 = 0 by -3. (Mar. ’06)
Solution:
Let f (x) ≡ x⁵ + 4x³ – x² + 11
The required equation is f(x + 3) = 0

The required equation is
x⁵ + 15x⁴ + 94x³ + 305x² + 507x + 353 = 0

Question 23.
Solve the equation 6x⁴ – 35x³ + 62x² – 35x + 6 = 0. (May. 13)
Solution:
We observe that the given equation is an even degree reciprocal equation of class one. On dividing both sides of the given equation by x², we get

Then the above equation reduces to
6(y² – 2) – 35y + 62 = 0
i.e., 6y² – 35y + 50 = 0
i.e., (2y – 5)(3y – 10) = 0.
Hence the roots of 6y² – 35y + 50 = 0 are \(\frac{5}{2}\) and \(\frac{10}{3}\).

Hence the roots of the given equation are \(\frac{1}{2}\), \(\frac{1}{3}\), 2 and 3.

Question 24.
Solve x⁵ – 5x⁴ + 9x³ – 9x² + 5x – 1 = 0. (Mar. ’13)
Solution:
Given equation is
x⁵ – 5x⁴ + 9x³ – 9x² + 5x – 1 = 0 is a reciprocal equation of odd degree and of class two.
∴ 1 is a root of the given equation.
⇒ (x – 1) is a factor of
x⁵ + 4x³ + 5x² – 4x² + 1 = 0

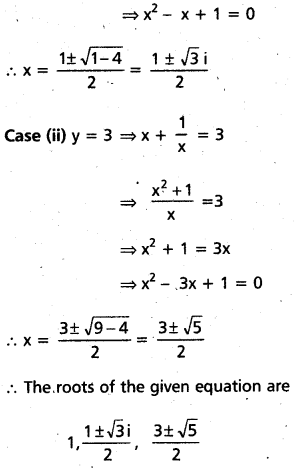
Question 25.
Form the polynomial equation of degree 3 whose roots are 2, 3 and 6. (Mar. ’02)
Solution:
The required polynomial equation is,
(x – 2) (x – 3)(x – 6) = 0
⇒ x³ – 11x³ + 36x – 36 = 0

Question 26.
Find the relation between the roots and the coefficients of the cubic equation
3x³ – 10x² + 7x + 10 = 0.
Solution:
3x³ – 10x² + 7x + 1o = 0 ———- (1)
On.comparing (1) with
ax³ + bx² + cx + d = 0,
we have

Question 27.
Write down the relations between the roots and the coefficients of the bi-quadratic equation.
x⁴ – 2x³ + 4x² + 6x – 21 = 0
Solution:
Given equation is
x⁴ – 2x³ + 4x² + 6x – 21 = 0 —— (1)
On comparing (1) with
ax⁴ + bx³ + cx² + dx + c = 0,
we have

Question 28.
If 1, 2, 3 and 4 are the roots of x⁴ + ax³ + bx² + cx + d = 0, then find the
values of a, b, c and d.
Solution:
Given that the roots of the given equation are 1, 2, 3 and 4. Then
x⁴ + ax³ + bx² + cx + d
≡ (x – 1) (x – 2) (x – 3) (x – 4) = 0
≡ x⁴ – 10x³ + 35x² – 50x + 24 = 0
On equating the coefficients of like powers of x, we obtain
a = -10, b = 35, c = -50, d = 24

Question 29.
if a, b, c are the roots of
x³ – px² + qx- r = 0 and r ≠ 0, then find \(\frac{1}{\mathbf{a}^{2}}+\frac{1}{\mathbf{b}^{2}}+\frac{1}{\mathrm{c}^{2}}\) interms of p, q, r.
Solution:
Given that a, b, c are the roots of
x³ – px² + qx – r = 0, then
a + b + c = p, ab + bc + ca = q, abc = r

Question 30.
Find the sum of the squares and the sum of the cubes of the roots of the equation x³ – px² + qx – r = 0 in terms of p, q, r.
Solution:
Let α, β, γ be the roots of the given equation then α + β + γ = p, αβ + βγ + γα = q, αβγ = r
Sum of the squares of the roots is α² + β² + γ²
= (α + β + γ)² – 2(αβ + βγ + γα) = p² – 2q
Sum of the cubes of the roots is α³ + β³ + γ³
= (α + β + γ) (α² + β² + γ² – αβ – βγ – γα) + 3αβγ
= p(p² – 2q – q) + 3r
= p(p² – 3q) + 3r

Question 31.
Obtain the cubic equation, whose roots are the sqüares of the roots of the equation, x³ + p₁x² + P₂x + p₃ = 0
Solution:
The required equation is, f(\(\sqrt{x}\)) =0

Question 32.
Let α, β, γ be the roots of
x³ + px² + qx + r = 0. Then find the
i) Σα²
ii) Σ\(\frac{1}{\alpha}\)
iii) Σα³
iv) Σβ²γ²
v) Σ(α + β) (β + γ) (γ + α)
Solution:
since α, β, γ are the roots of the equation, we have α + β + γ = – p,
αβ + βγ + γα = q, αβγ = -r.

i) Σα²
Solution:
Σα² = α² + β² + γ²
= (α + β + γ) – 2(αβ + βγ + γα)
= p² – 2q

ii) Σ\(\frac{1}{\alpha}\)
Solution:

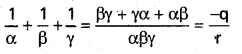
iii) Σα³
Solution:

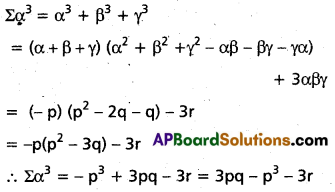
iv) Σβ²γ²
Solution:

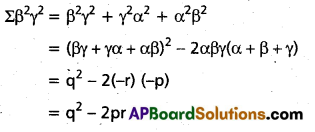
v) (α + β) (β + γ) (γ + α)
Solution:
We know, α + β + γ = -p
⇒ α + β = -p – r and β + γ = -p – α
= γ + α = -p – β
∴ (α + β) (β + γ)(γ + α)
= (-p – γ) (-p – α) (-p – β)
= -p³ – p²(α + β + γ) – p(αβ + βγ + γα) – αβγ
= -p³ + p³ – pq + r = r – pq .

Question 33.
Let α, β, γ be the roots of
x³ + ax² + bx + c = 0 then find Σα² + Σβ²
Solution:
Since α, β, γ are roots of the given equation,

Question 34.
If α, β, γ are the roots of x³ + px² + qx + r = 0, then form the cubic equation whose roots are .
α(β + γ), β(γ + α), γ(α + β)
Solution:
Let α, β, γ be the roots of the given equation.
we have, α + β + γ = – p, αβ + βγ + γα = q, αβγ = -r
Let y = α(β + γ)
= αβ + αγ + γβ – βγ

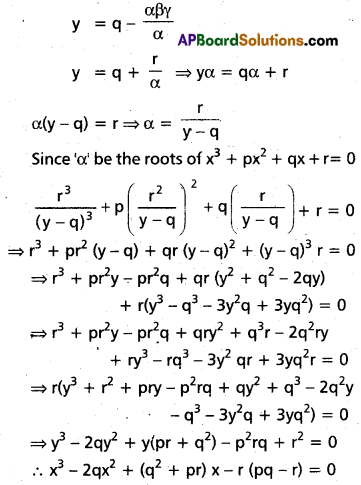
Question 35.
Solve x³ – 3x² – 16x + 48 = 0
Solution:
Let f(x) = x³ – 3x² – 16x + 48
by inspection, f(3) = 0
Hence 3 is a root of 1(x) = 0
Now we divide f(x) by (x – 3)

Question 36.
Find the roots of
x⁴ – 16x³ + 86x² – 176x + 105 = 0 (Mar. ‘02)
Solution:
Let f(x) = x⁴ – 16x³ + 86x² – 176x + 105
Now if (1) = 1 – 16 + 86 – 176 + 105 = 0
∴ 1 is a root of f(x) = 0
⇒ x – 1 is a factor of f(x)

∴ g(x) = (x – 3)(x² – 12x + 35)
= (x – 3) (x – 5) (x – 7)
∴ f(x) = (x – 1) (x – 3) (x – 5) (x – 7)
∴ 1, 3, 5, 7 are the roots of f(x) = 0.

Question 37.
Solve x³ – 7x² + 36 = 0, given one root being twice the other.
Solution:
Let α, β, γ be the root of the equation
x³ – 7x² + 36 = 0 and
let β = 2α
Now, we have, α + β + γ = 7
⇒ 3α + γ = 7 —— (1)
αβ + βγ + γα = 0
⇒ 2α² + 3αγ = 0 —— (2)
αβγ = -36 ⇒ 2α²γ = -36 —— (3)
From (1) and (2), we have
2α² + 3α(7 – 3α) = 0
i.e., α² – 3α = 0 (or) α(α – 3) = 0
∴ α = 0 or α = 3
Since α = 0 does not satisfy the given equation.
∴ α = 3, so β = 6 and γ = -2
∴ The roots are 3, 6, -2.

Question 38.
Given that 2 is a root of
x³ – 6x² + 3x + 1o = 0, find the other roots.
Solution:
Let f(x) = x³ – 6x² + 3x + 10
Since 2 is a root of f(x) = 0, we divide f(x) by (x – 2)

∴ -1, 2, and 5 are the roots of the given equation.

Question 39.
Given that two roots of
4x³ + 20x² – 23x + 6 = 0 are equal, find all the roots of the given equation.
Solution:
Let α, β, γ are the roots of
4x³ + 20x² – 23x + 6 = 0
Given two roots are equal, let α = β

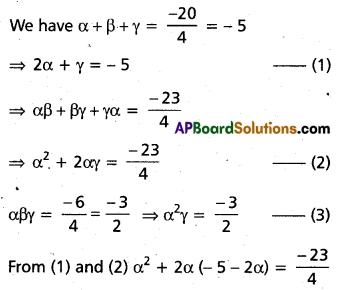
⇒ 12α² + 4α – 23 = 0
⇒ (2α – 1) (6α + 23) = 0
α = \(\frac{1}{2}\), α = \(\frac{-23}{6}\)
On verfication, we get that is a root of (1)
α = \(\frac{1}{2}\) is roots of (1)
(2) ⇒ roots are \(\frac{1}{2}\), \(\frac{1}{2}\), -6

Question 40.
Given that the sum of two roots of
x⁴ – 2x³ + 4x² + 6x – 21 = 0 is zero find the roots of the equation.
Solution:
Let α, β, γ, δ are the roots of given equation, since sum of two is zero.
α + β = 0
Now α + β + γ + δ = 2 ⇒ γ + δ = 2
Let αβ = p, γδ = q
The equation having the roots α, β is

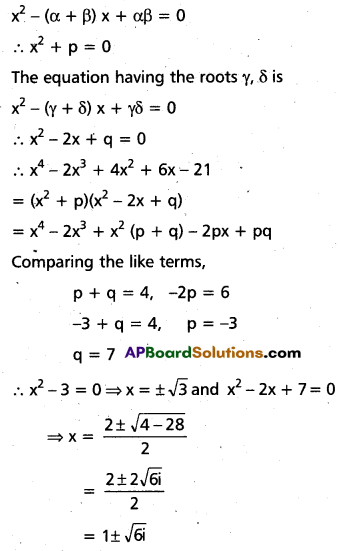
∴ Roots are –\(\sqrt{3}\), \(\sqrt{3}\), 1 – i \(\sqrt{6}\) and 1 + i \(\sqrt{6}\)

Question 41.
Solve 4x³ – 24x² + 23x + 18 = 0, given that the roots of this equation are in arithmetic progression. (Mar. 14, May ‘06)
Solution:
Let a – d, a, a + d are the roots of the given equation
Now, sum of the roots
a – d + a + a + d = \(\frac{24}{4}\)
3a = 6
a = 2
Product of the roots (a – d) a (a + d) = \(\frac{-18}{4}\)
a(a² – d²) = \(\frac{-9}{2}\)
2(4 – d²) = \(\frac{-9}{2}\)
4(4 – d²) = -9
16 – d² = -9
4d² = 25
d = ± \(\frac{5}{2}\)
∴ roots are –\(\frac{1}{2}\), 2 and \(\frac{9}{2}\)

Question 42.
Solve x³ – 7x² + 14x – 8 = 0, given that the roots are in geometric progression.
Solution:
Let \(\frac{a}{r}\), a, ar be the roots of the given equation. Then .

Hence a = 2. On substituting a = 2 in (1), we obtain
\(\frac{2}{r}\) + 2 + 2r = 7
i.e., 2r² – 5r + 2 = 0
i.e., (r – 2) (2r – 1) = 0
Therefore r = 2 or r = \(\frac{1}{2}\)
Hence the roots of the given equation are 1, 2 and 4.

Question 43.
Solve x⁴ – 5x³ + 5x² + 5x – 6 = 0 given that the product of two of its roots is 3.
Solution:
Let α, β, γ, δ be the roots of the given equation.
Product of the roots αβγδ = -6
Given αβ = 3 (∵ Product of two roots is 3)
∴ α, β, γ, δ = -6
γδ = -2
Let α + β, γ + δ = q
The equation having the roots α,β is
x² – (α + β) x + αβ = 0
x² + px + 3 = 0
The equation having the roots γ, δ is
x² – (γ + δ)x + γδ = 0
x² – qx – 2 = 0
∴ x⁴ – 5x³ + 5x² + 5x – 6
= (x² – px + 3)(x² – qx – 2)
= x⁴ – (p + q)x³ + (1 + pq)x² + (2p – 3q)x – 6
Comparing the like terms,
p + q = 5, 2p – 3q = 5
∴ 2p – 3q = 5
3p + 3q = 15
5p = 20 ⇒ p = 4
∴ q = 1
Now x² – 4x + 3 = 0 ⇒ (x – 3)(x – 1) = 0
⇒ x = 1, 3
x² – x – 2 = 0 ⇒ (x – 2)(x + 1) = 0
⇒ x = -1, 2
∴ The roots are -1, 2, 1, 3

Question 44.
Solve x⁶ + 4x³ – 2x² – 12x + 9 = 0, Given that it has two pairš of equal roots.
Solution:
Given equation is
x⁴ + 4x³ – 2x² – 12x + 9 = 0
Let the roots be α, α, β, β
Sum of the roots, 2(α + β) = -4
⇒ α + β = -2
Let αβ = p
The equation having roots α, β is
x² – (α + β)x + αβ = 0
i.e. x² + 2x + p = 0
∴ x⁴ + 4x³ – 2x² – 12x + 9
= [x² – (α + β)x + αβ]²
= (x² + 2x + p)²
= x⁴ + 4x³ + (2p + 4)x² + 4px + p²
Comparing coefficients of x on both sides
4p = -12 ⇒ p = – 3
x² + 2x + p = 0 ⇒ x² + 2x – 3 = 0
⇒ (x + 3)(x – 1) = 0
⇒ x = -3, 1
∴ The roots of the given equation are -3, -3, 1, 1

Question 45.
Prove that the sum of any two of the roots of the equation x⁴ + px³ + qx² + rx + s = 0 is equal to the sum of the remaining two roots of the equation iff p³ – 4pq + 8r = 0.
Solution:
Suppose that the sum of two of the roots of the given equation is equal to the sum of the remaining two roots.
Let α, β, γ, δ be roots of the given equation such that α + β = γ + δ

From these equations, we have

Then equations (1), (2) and (4) are satisfied. In view of (5), equation (3) is also satisfied. Hence (x² + bx + c)(x² + bx + d) = x⁴ + 2bx³ + (b² + c + d)x² + b(c + d)x + cd = x⁴ + px³ + qx² + rx + s
Hence the roots of the given equation are α₁, β₁, γ₁ and δ₁. where α₁ and β₁ are the roots of the equations x² + bx + c = 0 and γ₁ and δ₁ are those of the equation x² + bx + d = 0.
We have α₁ + β₁ = -b = γ₁ + δ₁.

Question 46.
Form the polynomial equation of degree 4 whose roots are
4 + \(\sqrt{3}\), 4 – \(\sqrt{3}\), 2 + i and 2 – i
Solution:
The equation having roots 4 + \(\sqrt{3}\), 4 – \(\sqrt{3}\) is
x² – 8x + 13 = 0
The equation having roots 2 + i, 2 – i is
x² – 4x + 5 = 0.
The required equation is
(x² – 8x + 13) (x² – 4x + 5) = 0
∴ x⁴ – 12x³ + 50x² – 92x + 65 = 0

Question 47.
Solve 6x⁴ – 13x³ – 35x² – x + 3 = 0 given that one of its root is 2 + \(\sqrt{3}\).
Solution:
2 + \(\sqrt{3}\) is a root 2 – \(\sqrt{3}\) is also a root.
The equation having roots

Question 48.
Find the polynomial equation of degree 4 whose roots are the negatives of the roots of x⁴ – 6x³ + 7x² – 2x + 1 = 0
Solution:
Let f(x) ≡ x⁴ – 6x³ + 7x² – 2x + 1
The required equation is f(-x) = 0
i.e., (-x)⁴ – 6(-x)³ + 7(-x)² + 2(-x) + 1 = 0
∴ x⁴ + 6x³ + 7x² + 2x + 1 = 0

Question 49.
Find the algebraic equation of the degree 4 whose roots are 3 times the roots of the equation
6x⁴ – 7x³ + 8x² – 7x + 2 = 0
Solution:
Let f(x) ≡ 6x⁴ – 7x³ + 8x² – 7x +2
The required equation is f\(\left(\frac{x}{3}\right)\) = o

Question 50.
Form the equation whose roots are m times the roots of the equation x³ + \(\frac{x^{2}}{4}\) – \(\frac{x}{16}\) + \(\frac{1}{72}\) = 0 and deduce the case when m = 12.
Solution:

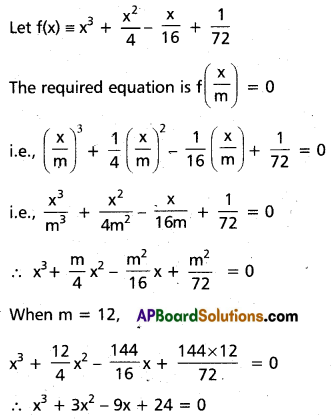
Question 51.
Find the algebraic equation of degree 5 whose roots are the translates of the roots of x⁵ + 4x³ – x² + 11 = 0 by -3. (Mar. ’06)
Solution:
Let f (x) ≡ x⁵ + 4x³ – x² + 11
The required equation is f(x + 3) = 0

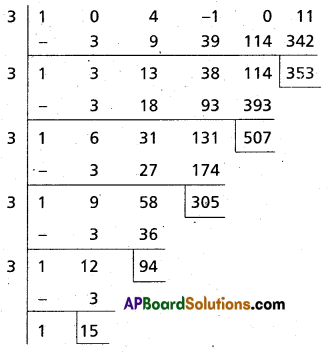
The required equation is
x⁵ + 15x⁴ + 94x³ + 305x² + 507x + 353 = 0

Question 52.
Find the algebraic equation of degree 4 whose roots are the translates of the roots
4x⁴ + 32x³ + 83x² + 76x + 21 = 0 by 2.
Solution:
Let f(x) ≡ 4x⁴ + 32x³ + 83x² + 76x + 21
The required equation is f(x – 2) = 0

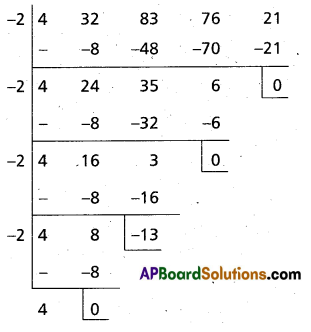
The required equation is
4x⁴ – 13x² + 9 = 0

Question 53.
Find the polynomial equation whose roots are the reciprocals of the roots of the equation
x⁴ + 3x³ – 6x² + 2x -4 = 0
Solution:
Let f(x) ≡ x⁴ + 3x³ – 6x² + 2x – 4

Question 54.
Find the polynomial equation whose roots are the squares of the roots of x³ – x² + 8x – 6 = 0
Solution:
Let f(x) ≡ x³ – x² + 8x – 6 .
The required equation is f(\(\sqrt{x}\)) = o

Squaring on both sides
⇒ x(x² + 16x + 64) = x² + 12x + 36
= x³ + 6x² + 64x – x² – 12x – 36 = 0
∴ x³ + 15x² + 52x – 36 = 0

Question 55.
Show that 2x³ + 5x² + 5x + 2 = 0 is a reciprocal equation of class one.
Solution:
Given equation is 2x³ + 5x² + 5x + 2 = 0
P₀ = 2, p₁ = 5, P₂ = 5, p₃ = 2
Here P₀ = p₃, p₁ = p₂
∴ The equation 2x³ + 5x² + 5x + 2 = 0 is a reciprocal equation of class one.

Question 56.
Solve the equation
4x³ – 13x² – 13x + 4 = 0
Solution:
4x³ – 13x² – 13x + 4 = 0 is a reciprocal equation of first class and of odd degree.
Thus -1 is a root of the 9iven equation.

4x² – 17x + 4 = 0 ⇒ 4x² – 16x – x + 4 = 0
⇒ 4x(x – 4) – 1 (x – 4) = 0
⇒ (x – 4)(4x – 1) = 0
⇒ x = 4 or \(\frac{1}{4}\)
The roots are -1, 4, \(\frac{1}{4}\)

Question 57.
Solve the equation 6x⁴ – 35x³ + 62x² – 35x + 6 = 0. (May ‘13)
Solution:
We observe that the given equation is an even degree reciprocal equation of class one.
On dividing both sides 6f the given equation by x², we get

Then the above equation reduces to
6(y² – 2) – 35y + 62 = 0
i.e., 6y² – 35y + 50 = 0
i.e., (2y – 5) (3y – 10) = 0.
Hence the roots of 6y² – 35y + 50 = 0 are \(\frac{5}{2}\) and \(\frac{10}{3}\).
Therefore x + \(\frac{1}{x}\) = \(\frac{5}{2}\) and x + \(\frac{1}{x}\) = \(\frac{10}{3}\)
i.e., 2x² – 5x + 2 = 0 and 3x² – 10x + 3 = 0.
The roots of these equations are respectively

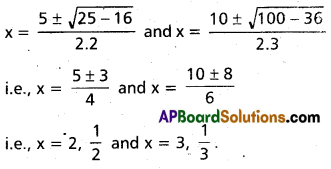
Hence the roots of the given equation are \(\frac{1}{2}\), \(\frac{1}{3}\), 2 and 3.

Question 58.
Solve x⁵ – 5x⁴ – 9x³ – 9x² + 5x – 1 = 0. (Mar ’13)
Solution:
Given equation is
x⁵ – 5x⁴ + 9x³ – 9x² + 5x – 1 = 0 is a reciprocal equation’of odd degree and of class two.
∴ 1 is a root of the given equation.
⇒ (x – 1) is a factor of
x⁵ – 5x⁴ + 9x³ – 9x² + 5x – 1 = 0

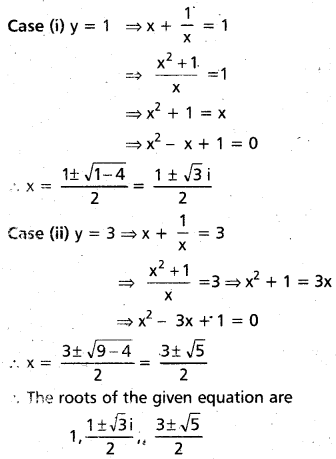
Question 59.
Solve the equation
6x⁶ – 25x⁵ + 31x⁴ – 31x² + 25x – 6 = 0
Solution:
Given equation is
6x⁶ – 25x⁵ + 31x⁴ – 31x² + 25x – 6 = 0 is a reciprocal equation of second class and of even degree.
∴ x² – 1 is a factor of
6x⁶ – 25x⁵ + 31x⁴ – 31x² + 25x – 6 = 0

∴ (1) becomes 6(y² – 2) – 25(y) + 37 = 0
⇒ 6y² – 12 – 25y + 37 = 0
⇒ 6y² – 25y + 25 = 0
⇒ 6y² – 15y – 10y + 25 = 0
⇒ 3y(2y – 5) – 5(2y – 5) = 0
⇒ (2y – 5)(3y – 5) = 0