Students get through Maths 2A Important Questions Inter 2nd Year Maths 2A Random Variables and Probability Distributions Important Questions which are most likely to be asked in the exam.
Intermediate 2nd Year Maths 2A Random Variables and Probability Distributions Important Questions
Question 1.
A Poisson variable satisfies P(X = 1) = P(X = 2). Find P(X = 5) (Mar.14; May ’13,’06).
Solution:

Question 2.
The probability that a person chosen at random is left handed (in hand writing) is 0.1. What is the probability that in a group of ten people there is one, who is left handed? (TS Mar.’16; AP Mar. ’17 ’15)
Solution:
Here n = 10
p = 0.1
q = 1 – p = 1 – 0.1 = 0.9
P(X = 1) = 10C1 (0.1)1 (0.9)10 – 1
= 10 × 0.1 × (0.9)
= 1 × (0.9)
= (0.9)
![]()
Question 3.
A Poisson variable satisfies P(X = 1) = P(X = 2). Find P(X = 5) (Mar.14; May ’13, ’06)
Solution:
Given P(X = 1) = P(X = 2)

Question 4.
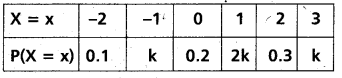
is the probability distribution of a random variable X. Find the value of K and the variance of X. ( March 2006) (TS Mar. 17)
Solution:
Sum of the probabilities = 1
0.1 + k + 0.2 + 2k + 0.3 + k = 1
4k + 0.6 = 1
4k = 1 – 0.6 = 0.4
k = \(\frac{0.4}{4}\) = 0.1
Mean = (-2) (0.1) + (-1) k + 0(0.2) + 1(2k) + 2(0.3) + 3k
= -0.2 – k + 0 + 2k + 0.6 + 3k
= 4k + 0.4
=4(0.1) + 0.4
= 0.4 + 0.4
= 0.8
μ = 0.8
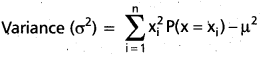
∴ Variance = 4(0.1) + 1(k) + 0(0.2) + 1(2k) + 4(0.3) + 9k – μ2
= 0.4 + k + 0 + 2k + 4(0.3) + 9k – μ2
= 12k + 0.4 + 1.2 – (0.8)2
= 12(0.1) + 1.6 – 0.64
= 1.2 + 1.6 – 0.64 .
∴ σ2 = 2.8 – 0.64 = 2.16
Question 5.
A random variable X has the following probability distribution. (TS & AP Mar. ‘16)
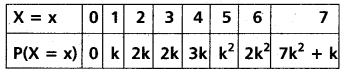
Find
i) k
ii) the mean and
iii) P(0 < X < 5).
Solution:
Sum of the probabilities = 1
⇒ 0 + k + 2k + 2k + 3k + k2 + 2k2 + 7k2 + k = 1
⇒ 10k2 + 9k = 1
⇒ 10k2 + 9k – 1 = 0
⇒ 10k(k + 1) – 1(k + 1) = 0
⇒ (10k – 1) (k + 1) = 0
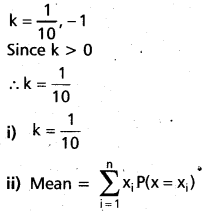
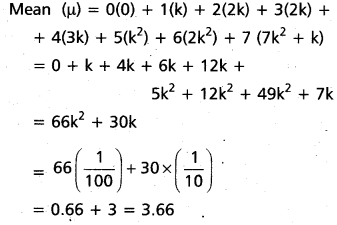
![]()
iii) P(0 < x < 5)
P(0 < x < 5) = P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)
= k + 2k + 2k + 3k
= 8k
= 8\(\frac{1}{10}\)
= \(\frac{8}{10}\) = \(\frac{4}{5}\)
Question 6.
The range of a random variable X is {0, 1, 2}. Given that P(X = 0) = 3c3, P(X = 1) = 4c – 10c2, P(X = 2) = 5c – 1
i) Find the value of c
ii) P(X < 1),P(1 < X ≤ 2) and P (0 < X ≤ 3) (AP & TS Mar. 15, 13, ‘11, 07, 05; May ‘11’)
Solution:
P(X = 0) + P(X = 1) + P(X = 2) = 1
3c3 + 4c – 10c2 + 5c – 1 = 1
3c3 – 10c2 + 9c – 2 = 0
c = 1 satisfy this equation
c = 1 ⇒ P(X = 0) = 3 which is not possible
Dividing with c – 1, we get
3c2 – 7c + 2 = 0
(c – 2) (3c – 1) = 0

ii) P(1 < X ≤ 2) = P(X = 2) = 5c – 1
= \(\frac{5}{3}\) – 1 = \(\frac{2}{3}\)
iii)P(0 < X ≤ 3) = P(X = 1) + P(X = 2)
= 4c – 10c2 + 5c – 1
= 9c – 10c2 – 1
= 9.\(\frac{1}{3}\) – 10.\(\frac{1}{9}\) – 1
= 3 – \(\frac{10}{9}\) – 1 = 2 – \(\frac{10}{9}\) = \(\frac{8}{9}\)
Question 7.
One in 9 ships is likely to be wrecked, when they are set on sail, when 6 ships are on sail, find the probability for
i) Atleast one will arrive safely
ii) Exactly, 3 will arrive safely. (Mar. 2008)
Solution:
p = probability of ship to be wrecked = \(\frac{1}{9}\)

Question 8.
If the mean and variance of a binomial variable X are 2.4 and 1.44 respectively, find P(1 < X ≤ 4). (May ’06)
Solution:
Mean = np = 2.4 …… (1)
Variance = npq = 1.44 …… (2)
Dividing (2) by (1),
\(\frac{\mathrm{npq}}{\mathrm{np}}\) = \(\frac{1.44}{2.4}\)
q = 0.6 = \(\frac{3}{5}\)
2
p = 1 – q = 1 – 0.6 = 0.4 = \(\frac{2}{5}\)
Substituting in (1)
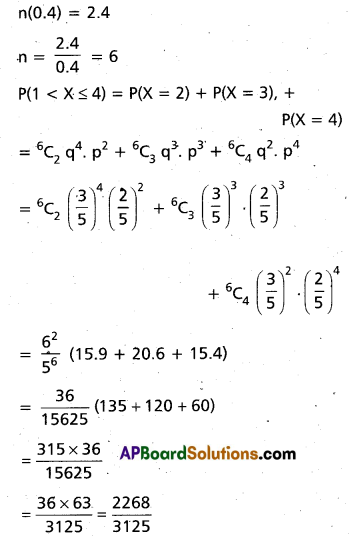
![]()
Question 9.
The probability distribution of a random variable X is given below. (AP Mar. ‘17’) (Mar. ‘14; May ‘13)

Find the value of K, and the mean and variance of X.
Solution:

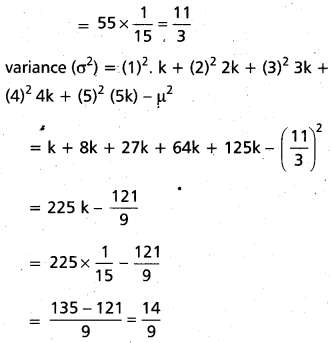
Question 10.
The mean and variance of a binomial distribution are 4 and 3 respectively. Fix the distribution and find P(X ≥ 1)
(AP Mar. ‘16 TS Mar. 17 ‘15, ’08)
Solution:
Given distribution ¡s Binomial distribution with mean = np = 4
variance = npq = 3
∴ \(\frac{n p q}{n p}\) = \(\frac{3}{4}\)
⇒ q = \(\frac{3}{4}\)
so that p = 1 – q
= 1 – \(\frac{3}{4}\) = \(\frac{1}{4}\)
∴ np = 4
n\(\frac{1}{4}\) = 4
⇒ n = 16

Question 11.
A cubical die is thrown. Find the mean and variance of X, giving the number on the face that shows up.
Solution:
Let S be the sample space and X be the random variable associated with S, where P(X) is given by the following table

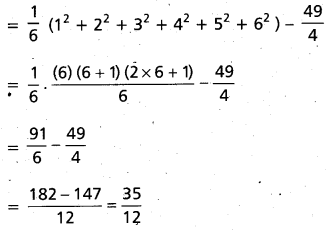
![]()
Question 12.
The probability distribution of a random variable X is given below.
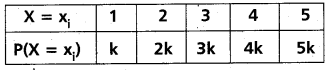
Find the value of k, and the mean and variance of X
Solution:

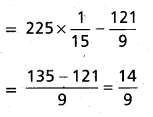
Question 13.
If x is a random variable with probability distribution. P(X = k) = \(\frac{(k+1) c}{2^{k}}\), k = 0, 1, 2 then find c.
Solution:

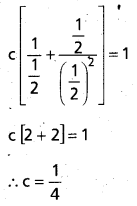
![]()
Question 14.
Let X be a random variable such that P(X = -2) =P(X = -1) = P(X = 2) = P(X = 1) = \(\frac{1}{6}\) and P(X = 0) = \(\frac{1}{3}\). Find the mean and variance of X.
Solution:
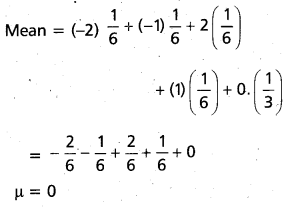
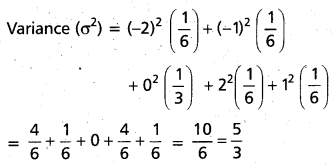
Question 15.
Two dice are rolled at random. Find the probability distribution of the sum of the numbers on them. Find the mean of the random variable.
Solution:
When two dice are rolled, the sample space
S contains 6 × 6 = 36 sample points.
S = {(1, 1), (1, 2) (1, 6), (2, 1), (2, 2) (6, 6)}
Let X denote the sum of the numbers on the tw0 dice.
Then the range of X = {2, 3, 4, ……… 12}
The Prob. distribution of X is given by the following table.

Question 16.
8 coins are tossed simultaneously. Find the probability of getting atleast 6 heads.
Solution:
p = Probability of getting head = \(\frac{1}{2}\)
q = 1 – p = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\) ; n = 8
P(X ≥ 6) = P(X = 6) + P(X = 7) + P(X = 8)

Question 17.
The mean and variance of a binomial distribution are 4 and 3 respectively. Fix the distribution and find P(X ≥ 1)
(A.P. Mar. ’16, T.S. Mar. ’15, ’08)
Solution:
Given distribution is Binomial distribution with mean = np = 4
variance = npq = 3
∴ \(\frac{n p q}{n p}\) = \(\frac{3}{4}\)
⇒ q = \(\frac{3}{4}\)
so that p = 1 – q
= 1 – \(\frac{3}{4}\) = \(\frac{1}{4}\)
∴ np = 4
n\(\frac{1}{4}\) = 4
⇒ n = 16

![]()
Question 18.
The probability that a person chosen at random is left handed (in hand writing) is 0.1. What is the probability that in a group of ten people there is one, who is left handed ? (Mar. 16, AP. Mar. ’15)
Solution:
Here n = 10
p = 0.1
q = 1 – p = 1 – 0.1 = 0.9
P(X = 1) = 10C1 (0.1)1 (0.9)10 – 1
= 10 × 0.1 × (0.9)
= 1 × (0.9)
= (0.9)
Question 19.
In a bõok of 450 pages, there are 400 typographical errors. Assumiñg that the number of errörs per page follow the
poisson law, find the probability that a random sample of 5 pages will contain no typographical error.
Solution:
The average number of errors per page in the book is
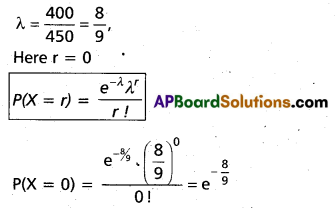
The required probability that a random sample of 5 pages will contain no error is
[P(X = 0)]5 = \(\left(e^{-8 / 9}\right)^{5}\)
Question 20.
Deficiency of red cells in the blood cells is determined by examining a specimen of blood under a microscope. Suppose a small fixed volume contains on an average 20 red cells for normal persons. Using the poisson distribution, find the probability that a specimen of blood taken from a normal person will contain less than 15 red cells.
Solution:
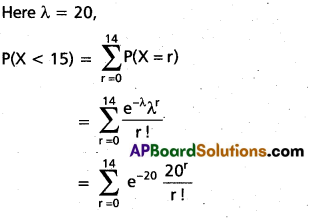
Question 21.
A Poisson variable satisfies P(X = 1) = P(X = 2). Find P(X = 5) (Mar. ‘14; May ‘06, ‘13)
Solution:
Given P(X = 1) = P(X = 2)
