Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A De Moivre’s Theorem Solutions Exercise 2(b) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2A De Moivre’s Theorem Solutions Exercise 2(b)
I. Find all the values of the following.
Question 1.
(i) (1 – i√3)1/3
Solution:

(ii) (-i)1/6
Solution:
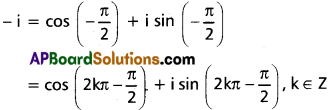

(iii) (1 + i)2/3
Solution:

(iv) (-16)1/4
Solution:

(v) (-32)1/5
Solution:

Question 2.
If A, B, C are angles of a triangle such that x = cis A, y = cis B, z = cis C, then find the value of xyz.
Solution:
∴ A, B, C are angles of a triangle
⇒ A + B + C = 180° ………..(1)
x = cis A, y = cis B, Z = cis C
xyz = cis (A + B + C)
= cos (A + B + C) + i sin (A + B + C)
= cos (180°) + i sin (180°)
= -1 + i(0)
= -1
∴ xyz = -1
![]()
Question 3.
(i) If x = cis θ, then find the value of \(\left[x^{6}+\frac{1}{x^{6}}\right]\)
Solution:
∵ x = cos θ + i sin θ
⇒ x6 = (cos θ + i sin θ)6 = cos 6θ + i sin 6θ
⇒ \(\frac{1}{x^{6}}\) = cos 6θ – i sin 6θ
∴ \(x^{6}+\frac{1}{x^{6}}\) = 2 cos 6θ
(ii) Find the cube roots of 8.
Solution:
Let x3 = 8
⇒ x = 81/3
⇒ x = (23)1/3 (1)1/3
⇒ x = 2 (1)1/3
Since cube roots of unity are 1, ω, ω2
∴ The cube roots or 8 are 2, 2ω, 2ω2
Question 4.
If 1, ω, ω2 are the cube roots of unity, then prove that
(i) \(\frac{1}{2+\omega}-\frac{1}{1+2 \omega}=\frac{1}{1+\omega}\)
Solution:
ω is a cube root of unity.
1 + ω + ω2 = 0 and ω3 = 1

(ii) (2 – ω) (2 – ω2) (2 – ω10) (2 – ω11) = 49
Solution:
∵ 1, ω, ω2 are the cube roots of unity.
ω3 = 1 and 1 + ω + ω2 = 0
2 – ω10 = 2 – ω9 . ω
= 2 – (ω3)3 ω
= 2 – (1)3 ω
= 2 – ω
and 2 – ω11 = 2 – (ω3)3 . ω2
= 2 – (1)3 ω2
= 2 – ω2
(2 – ω) (2 – ω2) = 4 – 2ω – 2ω2 + ω3
= 4 – 2(ω + ω2) + 1
= 4 – 2(-1) + 1
= 4 + 2 + 1
= 7
∴ (2 – ω) (2 – ω2) (2 – ω10) (2 – ω11) = (2 – ω) (2 – ω2) (2 – ω) (2 – ω2)
= ((2 – ω) (2 – ω2))2
= 72
= 49
(iii) (x + y + z) (x + yω + zω2) (x + yω2 + zω) = x3 + y3 + z3 – 3xyz
Solution:
∵ 1, ω, ω2 are the cube roots of unity.
⇒ 1 + ω + ω2 = 0 and ω3 = 1
Now consider,
(x + yω + zω2) (x + yω2 + zω)
= x2 + xyω2 + zxω + xyω + y2ω3 + yzω2 + zxω2 + yzω4 + z2ω3
= x2 + y2 (1) + z2 (1) + xy (ω + ω2) + yz (ω4 + ω2) + zx (ω + ω2)
= x2 + y2 + z2 + xy (-1) + yz (ω + ω2) + zx (-1)
= x2 + y2 + z2 – xy – yz – zx ……….(1)
L.H.S = (x + y + z) (x + yω + zω2) (x + yω2 + zω)
= (x + y + z) (x2 + y2 + z2 – xy – yz – zx) [by (1)]
= x3 + y3 + z3 – 3xyz
= R.H.S
![]()
Question 5.
Prove that -ω, and -ω2 are the roots of z2 – z + 1 =0, where ω and ω2 are the complex cube roots of unity.
Solution:
Since ω and ω2 are the complex cube roots of unity
∴ 1 + ω + ω2 = 0 and ω2 = 1
z2 – z + 1 = (-ω)2 – (-ω) + 1
= ω2 + ω + 1
= 0
∴ -ω is a root of the equation z2 – z + 1 = 0
z2 – z + 1 = (-ω2)2 – (-ω2) + 1
= ω4 + ω2 + 1
= ω3 . ω + ω2 + 1
= ω + ω2+ 1
= 0
∴ -ω2 is a root of the equation z2 – z + 1 = 0
Question 6.
If 1, ω, ω2 are the cube roots of unity, then find the values of the following.
(i) (a + b)3 + (aω + bω2)3 + (aω2 + bω)3
Solution:
Since 1, ω, ω2 are the cube roots of unity
∴ 1 + ω + ω2 = 0 and ω3 = 1
Now (a + b)3 = a3 + 3a2b + 3ab2 + b3 ……..(1)
(aω + bω2)3 = [ω(a + bω)]3
= ω3 (a + bω)3
= (1) (a + bω)3
= a3 + 3a2bω + 3ab2ω2 + b3ω3
= a3 + 3a2bω + 3ab2ω2 + b3 ……….(2)
∵ ω3 = 1
and (aω2 + bω)3 = [ω(aω + b)]3
= ω3 (aω + b)3
= (1) (aω + b)3
= a3ω3 + 3a2bω2 + 3ab2ω + b3
= a3(1) + 3a2bω2 + 3ab2ω + b3
∴ (aω2 + bω)3 = a3 + 3a2bω2 + 3ab2ω + b3 ……….(3)
Adding (1), (2) and (3)
(a + b)3 + (aω + bω2)3 + (aω2 + bω)3 = 3a3 + 3a2b (1 + ω + ω2) + 3ab2 (1 + ω + ω2) + 3b3
= 3(a3 + b3) + 3a2b (0) + 3ab2 (0)
= 3(a3 + b3)
∴ (a + b)3 + (aω + bω2)3 + (aω2 + bω)3 = 3 (a3 + b3)
(ii) (a + 2b)2 + (aω2 + 2bω)2 + (aω + 2bω2)2
Solution:
(a + 2b)2 = a2 + 4ab + 4b2 ……….(1)
(aω2 + 2bω)2 = a2ω4 + 4abω3 + 4b2ω2
= a2ω3ω + 4ab (1) + 4b2ω2
= a2ω + 4ab + 4b2ω2 ………..(2)
and (aω + 2bω2)2 = a2ω2 + 4abω3 + 4b2ω4
= a2ω2 + 4ab (1) + 4b2ω3ω
= a2ω2 + 4ab + 4b2 (1) ω
∴ (aω + 2bω2)2 = a2ω2 + 4ab + 4b2ω ……….(3)
By Adding (1), (2) and (3)
(a + 2b)2 + (aω2 + 2bω)2 + (aω + 2bω2)2
= a2 (1 + ω + ω2) + 12ab + 4b2 (1 + ω + ω2)
= a2 (0) + 12ab + 4b2 (0)
= 12ab
∴ (a + 2b)2 + (aω2 + 2bω)2 + (aω + 2bω2)2 = 12ab
![]()
(iii) (1 – ω + ω2)3
Solution:
(1 – ω + ω2)3 = (-ω – ω)3
= (-2ω)3
= -8ω3
= -8(1)
= -8 (∵ 1 + ω + ω2 = 0)
(iv) (1 – ω) (1 – ω2) (1 – ω4) (1 – ω8)
Solution:
1 – ω4 = 1 – (ω3) ω
= 1 – (1) ω
= 1 – ω
1 – ω8 = 1 – (ω3)2 ω2
= 1 – (1) ω2
= 1 – ω2
∴ (1 – ω) (1 – ω2) (1 – ω4)(1 – ω8) = (1 – ω) (1 – ω2) (1 – ω) (1 – ω2)
= [(1 – ω) (1 – ω2)]2
= (1 – ω – ω2 + ω3)2
= [1 – (ω + ω2) + 1] (∵ 1 + ω + ω2 = 0)
= [1 – (-1) + 1]2
= (3)2
= 9
∴ (1 – ω) (1 – ω2) (1 – ω4) (1 – ω8) = 9
(v) \(\left[\frac{a+b \omega+c \omega^{2}}{c+a \omega+b \omega^{2}}\right]+\left[\frac{a+b \omega+c \omega^{2}}{b+c \omega+a \omega^{2}}\right]\)
Solution:
∴ 1, ω, ω2 are the cube roots of unity
⇒ ω3 = 1 and 1 + ω + ω2 = 0 ………..(1)
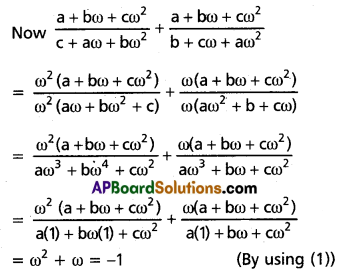
(vi) (i + ω)3 + (1 + ω2)3
Solution:
(i + ω)3 + (1 + ω2)3 = (-ω2)3 +(-ω)3
= -ω6 – ω3
= -1 – 1
= -2
∴ (1 + ω)3 + (1 + ω2)3 = -2
(vii) (1 – ω + ω2)5 + (1 + ω – ω2)5
Solution:
(1 – ω + ω2)5 + (1 + ω – ω2)5 = (-ω – ω)5 + (-ω2 – ω2)5
= (-2ω)5 + (-2ω2)5
= -32ω5 – 32ω10
= -32(ω5 + ω10)
= -32(ω2 + ω)
= -32(-1)
= 32
∴ (1 – ω + ω2)5 + (1 + ω – ω2)5 = 32
II.
Question 1.
Solve the following equations.
(i) x4 – 1 = 0
Solution:
x4 – 1 = 0
⇒ x4 = 1
⇒ x4 = cos 0° + i sin 0°
⇒ x4 = cos 2kπ + i sin 2kπ
⇒ x = (cos 2kπ + i sin 2kπ)1/4
= cos \(\frac{k \pi}{2}\), k = 0, 1, 2, 3
i.e., cos 0° + i sin 0°, cos \(\frac{\pi}{2}\) + i sin \(\frac{\pi}{2}\), cos π + i sin π, cos \(\frac{3 \pi}{2}\) + i sin \(\frac{3 \pi}{2}\),
i.e., 1, i, -1, -i = ±1, ±i
(ii) x5 + 1 = 0
Solution:
x5 + 1 = 0
⇒ x5 = -1
⇒ x5 = cos π + i sin π
⇒ x5 = cos(2k + 1) π + i sin(2k + 1) π, k ∈ z
⇒ x = [cos(2k + 1) π + i sin(2k + 1) π]1/5
⇒ x = cis \(\frac{(2 k+1) \pi}{5}\), k = 0, 1, 2, 3, 4
(iii) x9 – x5 + x4 – 1 = 0
Solution:
x9 – x5 + x4 – 1 = 0
⇒ x5 (x4 – 1) + 1 (x4 – 1) = 0
⇒ (x4 – 1) (x5 + 1) = 0
⇒ x4 – 1 = 0
Solving the roots are ±1, ±i
(see the above problem)
x5 + 1 = 0
Solving the roots are cis \(\frac{(2 k+1) \pi}{5}\)
k = 0, 1, 2, 3, 4 (see the above problem)
∴ The roots of the given equation are ±1, ±i, cis (2k + 1) \(\frac{\pi}{5}\), k = 0, 1, 2, 3, 4
i.e., ±1, ±i, cis(\(\pm \frac{\pi}{5}\)), cis(\(\pm \frac{3 \pi}{5}\))
(iv) x4 + 1 = 0
Solution:
x4 + 1 = 0
⇒ x4 = -1
⇒ x4 = cos π + i sin π
∴ x4 = cos(2kπ + π) + i sin(2kπ + π),
∴ x = [cis(2k + 1)π]1/4
= cis(2k + 1) \(\frac{\pi}{4}\), where k = 0, 1, 2, 3
∴ x = \({cis} \frac{\pi}{4}, {cis}\left(\frac{3 \pi}{4}\right), {cis}\left(\frac{5 \pi}{4}\right)\) and \({cis}\left(\frac{7 \pi}{4}\right)\)
These four values of x are the solutions to the given equation.
![]()
Question 2.
Find the common roots of x12 – 1 = 0 and x4 + x2 + 1 = 0
Solution:
Consider x12 – 1 = 0
⇒ x12 = 1
⇒ x12 = (cos 0 + i sin 0)
⇒ x12 = (cos 2kπ + i sin 2kπ), k is a positive integer
⇒ x = (cos 2kπ + i sin 2kπ)1/2


Question 3.
Find the number of 15th roots of unity, which are also the 25th roots of unity.
Solution:
The number of common roots = H.C.F of {15, 25} = 5
Question 4.
If the cube roots of unity are 1, ω, ω2, then find the roots of the equation (x – 1)3 + 8 = 0.
Solution:
Given (x – 1)3 + 8 = 0
⇒ (x – 1)3 = -8
⇒ (x – 1)3 = (-2)3 (1)3
⇒ (x – 1) = (-2) (1)1/3
⇒ x – 1 = -2, -2ω, -2ω2
⇒ x = 1 – 2, 1 – 2ω, 1 – 2ω2
⇒ x = -1, 1 – 2ω, 1 – 2ω2
![]()
Question 5.
Find the product of all the values of (1 + i)4/5.
Solution:
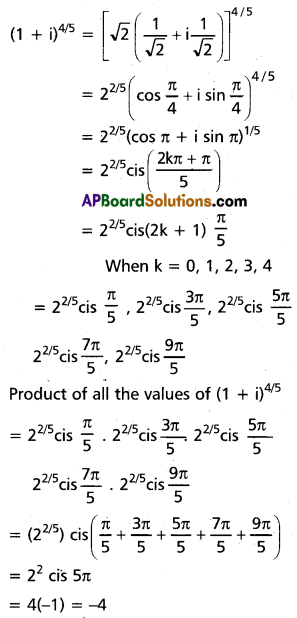
Question 6.
If z2 + z + 1 =0, where z is a complex number, prove that
\(\left(z+\frac{1}{z}\right)^{2}+\left(z^{2}+\frac{1}{z^{2}}\right)^{2}+\left(z^{3}+\frac{1}{z^{3}}\right)^{2}\) + \(\left(z^{4}+\frac{1}{z^{4}}\right)^{2}+\left(z^{5}+\frac{1}{z^{5}}\right)^{2}+\left(z^{6}+\frac{1}{z^{6}}\right)\) = 12
Solution:
Given z2 + z + 1 = 0
⇒ z = \(\frac{-1 \pm \sqrt{1-4.1 .1}}{2}\)
= \(\frac{-1 \pm i \sqrt{3}}{2}\)
= \(\frac{-1+i \sqrt{3}}{2}, \frac{-1-i \sqrt{3}}{2}\)
= ω, ω2
∴ 1 + ω + ω2 = 0 and ω3 = 1
If z = ω then

= (ω + ω2)2 + (ω2 + ω)2 + (1 + 1)2 + (ω + ω2)2 + (ω2 + ω)2 + (1 + 1 )2
= (-1)2 + (-1)2 + 4 + (-1)2 + (-1)2 + 4
= 1 + 1 + 4 + 1 + 1 + 4
= 12
Similarly If z = ω2 then
\(\left(z+\frac{1}{z}\right)^{2}+\left(z^{2}+\frac{1}{z^{2}}\right)^{2}+\left(z^{3}+\frac{1}{z^{3}}\right)^{2}\) + \(\left(z^{4}+\frac{1}{z^{4}}\right)^{2}+\left(z^{5}+\frac{1}{z^{5}}\right)^{2}+\left(z^{6}+\frac{1}{z^{6}}\right)\) = 12
III.
Question 1.
If 1, α, α2, α3, ……., αn-1 be the nth roots of unity, then prove that 1p + αp + (α2)p + (α3)p + …… + (αn-p)2p = 0
= 0; if p ≠ kn
= n; if p ≠ kn, where p, k ∈ N
Solution:
nth roots of unity are 1, α, α2, ………., αn-1


∴ Each term of the series in (1) is 1
Hence the sum of the series 1 + αp + (α2)p + (α3)p + …….. + (αn-1)p
= 1 + 1 + 1 + ……… + 1 (n times)
= n(1)
= n
![]()
Question 2.
Prove that the sum of 99th powers of the roots of the equation x7 – 1 = 0 is zero and hence deduce the roots of x6 + x5 + x4 + x3 + x2 + x + 1 = 0.
Solution:


Question 3.
If n is a positive integer, show that \((p+i q)^{1 / n}+(p-i q)^{1 / n}=2\left(p^{2}+q^{2}\right)^{1 / 2 n}\) . \(\cos \left(\frac{1}{n}, \tan \frac{q}{p}\right)\)
Solution:


Question 4.
Show that one value of \(\left(\frac{1+\sin \frac{\pi}{8}+i \cos \frac{\pi}{8}}{1+\sin \frac{\pi}{8}-i \cos \frac{\pi}{8}}\right)^{8 / 3}\) is -1.
Solution:
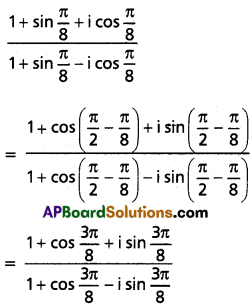

![]()
Question 5.
Solve (x – 1)n = xn, n is a positive integer.
Solution:
Since x = 0 is not a solution of the given equation, it is equivalent to the equation \(\left(\frac{x-1}{x}\right)^{n}=1\)
Clearly \(\left(\frac{x-1}{x}\right)^{n}=1\)
⇒ \(\frac{x-1}{x}\) is an nth root of unity other than one.
Suppose that ω is an nth root of unity and ω ≠ 1.
Then, \(\frac{x-1}{x}\) = ω
⇒ x – 1 = xω
⇒ (1 – ω) x = 1
⇒ x = \(\frac{1}{1-\omega}\), (∵ ω ≠ 1) ……….(1)

