Students get through Maths 2A Important Questions Inter 2nd Year Maths 2A Binomial Theorem Important Questions which are most likely to be asked in the exam.
Intermediate 2nd Year Maths 2A Binomial Theorem Important Questions
Question 1.
Find the number of terms in the expression of (2x + 3y + z)7 [Mar. 14, 13, 07]
Solution:
Number of terms in (a + b + c)n are \(\frac{(n+1)(n+2)}{2}\), where n is a postive integer. Hence number of terms in (2x + 3y + z)7 are \(\frac{(7+1)(7+2)}{2}=\frac{8 \times 9}{2}\) = 36
Question 2.
Prove that C0 + 2 . C1 + 4 . C2 + 8 . C3 + …………… + 2n . Cn = 3n [A.P. Mar. 15; May 07]
Solution:
L.H.S. = C0 + 2 . C1 + 4 . C2 + 8 . C3 + …………… + 2n . Cn
= 0 + C1(2) + C2 (2)2 + C3 (23) + …………… + Cn . 2n
= (1 + 2)n = 3n
Note: (1 + x)n = C0 + C1 . x + C2 . x2 + …………… + Cn . xn
Question 3.
If 22Cr is the largest binomial coefficient in the expansion of (1 + x)22, find the value of 13Cr. [A.P. Mar. 15; May 07]
Solution:
Here n = 22 is an even integer. There is only one largest binomial coefficient and it is
nC(n/2) = 22C11 = 22Cr ⇒ r = 11
∴ 13Cr = 13C11 = 13C2 = \(\frac{13 \times 12}{1 \times 2}\) = 78
Question 4.
Write down and simplify 6th term in (\(\frac{2x}{3}\) + \(\frac{3y}{2}\))9 [May 13]
Solution:
6th term in (\(\frac{2x}{3}\) + \(\frac{3y}{2}\))9
The general term in (\(\frac{2x}{3}\) + \(\frac{3y}{2}\))9 is
Tr+1 = 9Cr (\(\frac{2x}{3}\))9-r (\(\frac{3y}{2}\))r
Put r = 5
T6 = 9C5 (\(\frac{2x}{3}\))4 (\(\frac{3y}{2}\))5
= 9C5 (\(\frac{2}{3}\))4 (\(\frac{3}{2}\))5 x4 y5
= \(\frac{9 \times 8 \times 7 \times 6}{1 \times 2 \times 3 \times 4} \frac{\left(2^{4}\right)}{3^{4}} \cdot \frac{3^{5}}{2^{5}} \cdot x^{4} y^{5}\)
= 189 x4y5
Question 5.
If the coefficients of (2r + 4)th term and (3r + 4)th term in the expansion of (1 + x)21 are equal, find r. [T.S. Mar.15]
Solution:
T2r+4 in (1 + x)21 is
= 21C2r+3 (x)2r+3 ………………… (1)
T3r+4 in (1 + x)21 is
= 21C3r+3 . (x)3r+3 ……………….. (2)
⇒ Coefficients are equal
⇒ 21C2r+3 = 21C3r+3
⇒ 21 = (2r + 3) + (3r + 3)
(or)
2r + 3 = 3r + 3
⇒ 5r = 15
⇒ r = 3 (or) r = 0 .
Hence r = 0, 3.
![]()
Question 6.
Fin the sum of the infinite series 1 + \(\frac{1}{3}\) + \(\frac{1.3}{3.6}\) + \(\frac{1.3.5}{3.6.9}\) + …………… [T.S. Mar. 15]
Solution:
The series can be written as
S = 1 + \(\frac{1}{1}\). \(\frac{1}{3}\) + \(\frac{1.3}{3.6}\) (\(\frac{1}{3}\))2 + \(\frac{1.3.5}{1.2.3}\) (\(\frac{1}{3}\))3 + ……………..
The series of the right is of the form
1 + \(\frac{p}{1}\) (\(\frac{x}{q}\)) + \(\frac{p(p+q)}{1.2}\) (\(\frac{x}{q}\))2 + \(\frac{p(p+q)(p+2 q)}{1.2 .3}\) (\(\frac{x}{q}\))3 + ……………
Here p = 1, q = 2, \(\frac{x}{q}\) = \(\frac{1}{3}\) ⇒ x = \(\frac{2}{3}\)
The sum of the given series
S = (1 – x)-p/q
= (1 – \(\frac{2}{3}\))-1/2 = (\(\frac{1}{3}\))-1/2 = \(\sqrt{3}\)
Question 7.
Find the set E of the value of x for which the binomial expansions for the (a + bx)r are valid. [Mar. 08]
Solution:
(4 + 9x)-2/3 = 4-2/3 [1 + \(\frac{9x}{4}\)]-2/3
The binomial expansion of (4 + 9x)-2/3 is valid
When |\(\frac{9x}{4}\)| < 1
⇒ |x| < \(\frac{4}{9}\)
⇒ x ∈ (\(\frac{-4}{9}\), \(\frac{4}{9}\))
i.e., E = (\(\frac{-4}{9}\), \(\frac{4}{9}\))
Question 8.
If the 2nd, 3rd and 4th terms in the expansion of (a + x)n are respectively 240, 720,
1080, find a, x, n. [T.S. Mar. 16]
Solution:
T2 = 240 ⇒ nC1 an-1 x = 240 …………….. (1)
T3 = 720 ⇒ nC2 an-2 x2 = 720 …………… (2)
T4 = 1080 ⇒ nC3 an-3 x3 = 1080 …………… (3)
\(\frac{(2)}{(1)} \Rightarrow \frac{{ }^{n} C_{2} a^{n-2} x^{2}}{{ }^{n} C_{1} a^{n-1} x}=\begin{aligned}
&720 \\
&240
\end{aligned}\)
⇒ \(\frac{n-1}{2} \frac{x}{a}\) = 3 ⇒ (n – 1)x = 6a …………………. (4)
\(\frac{(3)}{(2)} \Rightarrow \frac{{ }^{n} C_{3} a^{n-3} x^{3}}{{ }^{n} C_{2} a^{n-2} x^{2}}=\frac{1080}{720}\)
⇒ \(\frac{n-2}{3} \frac{x}{a}=\frac{3}{2}\)
⇒ 2(n – 2)x = 9a …………………… (5)
\(\frac{(4)}{(5)} \Rightarrow \frac{(n-1) x}{2(n-2) x}=\frac{6 a}{9 a} \Rightarrow \frac{n-1}{2 n-4}=\frac{2}{3}\)
⇒ 3n – 3 = 4n – 8
⇒ n = 5
From (4), (5 – 1) x = 6a ⇒ 4x = 6a
⇒ x = \(\frac{3}{2}\) a
Substitute x = \(\frac{3}{2}\) a, n = 5 in (1)
5C1 . a4 . \(\frac{3}{2}\) a = 240
5 × \(\frac{3}{2}\) a5 = 240
a5 = \(\frac{480}{15}\) = 32 = 25
∴ a = 2, x = \(\frac{3}{2}\) a = \(\frac{3}{2}\) (2) = 3
∴ a = 2, x = 3, n = 5.
Question 9.
If the coefficients of rth, (r + 1)th, and (r + 2)nd, terms in the expansion of (1 + x)n, are in A.P. then show that n2 – (4r + 1)n + 4r2 – 2 = 0. [T.S. Mar. 15, 08]
Solution:
Coefficient of Tr = nCr-1
Coefficient of Tr+1 = nCr
Coefficient of Tr+2 = nCr+1
Given nCr-1, nCr, nCr+1 are in A.P.
⇒ 2 . nCr = nCr-1 + nCr+1

⇒ (2n – 3r + 2) (r + 1) = (n – r) (n – r + 1)
⇒ 2nr + 2n – 3r2 – 3r + 2r + 2 = n2 – 2nr + r2 + n – r
⇒ n2 – 4nr + 4r2 – n – 2 = 0
∴ n2 – (4r + 1)n + 4r2 – 2 = 0
Question 10.
If n is a postive integer, prove that \(\sum_{r=1}^{n} r^{3}\left(\frac{{ }^{n} C_{r}}{{ }^{n} C_{r-1}}\right)^{2}=\frac{(n)(n+1)^{2}(n+2)}{12}\) [Mar. 13]
Solution:
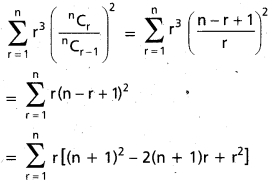
= (n + 1)2 Σ r – 2(n + 1) Σ r2 + Σ r3
= (n + 1)2 \(\frac{(n)(n+1)}{2}\)

![]()
Question 11.
Find the set of values of x for which the binomial expansions of the following are valid.
(i) (2 + 3x)-2/3
(ii) (5 + x)3/2
(iii) (7 + 3x)-5
(iv) (4 – \(\frac{x}{3}\))-1/2 [A.P. Mar. 17; Mar. 16; Mar. 11]
Solution:
(i) (2 + 3x)-2/3 = [2(1 + \(\frac{3}{2}\)x)]-2/3
= 2-2/3 (1 + \(\frac{3}{2}\)x)-2/3
∴ The binomial expansion of (2 + 3x)-2/3 is valid when |\(\frac{3}{2}\)x| < 1
(i.e.,) |x| < \(\frac{2}{3}\)
(i.e.,) x ∈ (-\(\frac{2}{3}\), \(\frac{2}{3}\))
ii) (5 + x)3/2 = [5 (1 + \(\frac{x}{5}\))]3/2 [T.S. Mar. 17]
= 53/2 (1 + \(\frac{x}{5}\))]3/2
∴ The binomial expansion of (5 + x)3/2 is valid when \(\frac{x}{5}\) < 1
(i.e.,) |x| < 5
(i.e.,) x ∈ (-5, 5)
iii) (7 + 3x)-5 = [7 (1 + \(\frac{3}{7}\) x)]-5
= 7-5 (1 + \(\frac{3}{7}\) x)]-5
(7 + 3x)-5 is valid when \(\frac{3x}{7}\) < 1
⇒ |x| < \(\frac{7}{3}\) ⇒ x ∈ (\(\frac{-7}{3}\), \(\frac{7}{3}\))
iv) (4 – \(\frac{x}{3}\))-1/2 = [4(1 – \(\frac{x}{3}\))]-1/2
(4 – \(\frac{x}{3}\))-1/2 is valid when \(\frac{-x}{12}\) < 1
⇒ |x| < 12
⇒ x ∈ (-12, 12)
Question 12.
Find the sum of the infinite series
\(\frac{3}{4}\) + \(\frac{3.5}{4.8}\) + \(\frac{3.5 .7}{4.8 .12}\) + …… (Mar. 11)
Solution:

Question 13.
If x = \(\frac{1.3}{3.6}\) + \(\frac{1.3 .5}{3.6 .9}\) + \(\frac{1.3 .5 .7}{3.6 .9 .12}\) + …… then prove that 9x2 + 24x = 11 (TS Mar. ’16, AP Mar. ’17, ’15)
Solution:
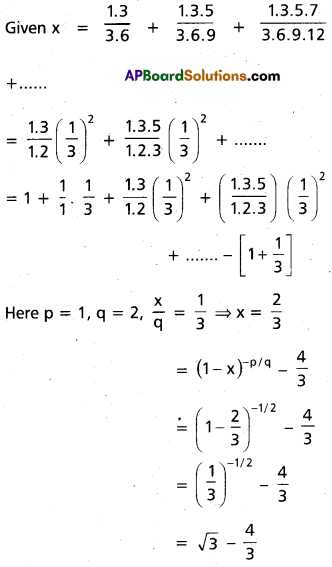
⇒ 3x + 4 = 3\(\sqrt{3}\)
Squaring on both sides
(3x + 4)2 = (3\(\sqrt{3}\))2
⇒ 9x2 + 24x + 16 = 27
⇒ 9x2 + 24x = 11
Question 14.
If x = \(\frac{5}{(2 !) \cdot 3}\) + \(\frac{5.7}{(3 !) \cdot 3^{2}}\) + \(\frac{5.7 .9}{(4 !) \cdot 3^{3}}\) + …… then find the value of x2 + 4x. (mar. 13)
Solution:
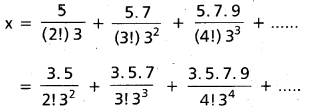

![]()
Question 15.
Find the sum of the infinite series
\(\frac{7}{5}\) (1 + \(\frac{1}{10^{2}}\) + \(\frac{1.3}{1.2}\).\(\frac{1}{10^{4}}\) + \(\frac{1.3 .5}{1.2 .3}\).\(\frac{1}{10^{6}}\) + …….) (AP Mar. ‘16, May 13; Mar. ’05)
Solution:

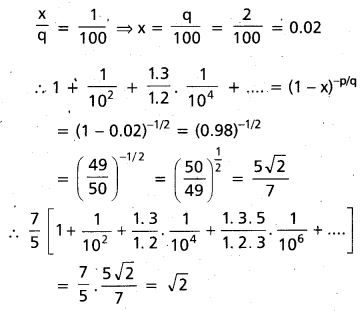
Question 16.
For n = 0, 1, 2, 3, ….n, prove that
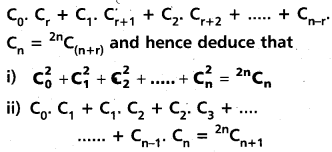
(TS Mar. ’15)
Solution:


Question 17.
If x = \(\frac{1}{5}\) + \(\frac{1.3}{5.10}\) + \(\frac{1.3 .5}{5.10 .15}\) + …… ∞ find 3x2 + 6x. (May. ’14, ’07, ’06; May. ’11)
Solution:
Given that
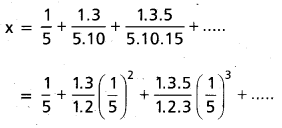
⇒ 3(1 + x)2 = 5
⇒ 3x2 + 6x + 3= 5
⇒ 3x2 + 6x = 2
Question 18.
Write the expansion or (2a + 3b)6.
Solution:

Question 19.
Find the 5th term in the expansion of (3x – 4y)7.
Solution:
T5 = T4 + 1
= 7C4 (3x)7 – 4 (-4y)4
= 35.27x3. 256y4
= 241920 x3 y4
![]()
Question 20.
Find the 4th term from the end in the expansion (2a + 5b)8.
Solution:
(2a + 5b)8 expansion contain 9 terms. The fourth term from the end is 6th term from the beginning.
∴ 8C5 (2a)8 – 5 (5b)5
= 8C5 (2a)8 – 5 (5b)5
= 8C5 . 23. 55 a3 b5
Question 21.
Find the middle term of the following expansions
(i) (3a – 5b)6
(ii) (2x + 3y)7
Solution:
i) Here n = 6 (even)
∴ \(\frac{n}{2}\) + 1 = \(\frac{6}{2}\) + 1 = 4th term is the middle term
∴ T4 = T3 + 1
= 6C3 (3a)6 – 3 (-5b)3,
= –6C3. 33. 53. a3 b3
ii) Here n = 7 (odd)
\(\frac{\mathrm{n}+1}{2}\) = \(\frac{7+1}{2}\) = 4, \(\frac{\mathrm{n}+3}{2}\) = \(\frac{7+3}{2}\) = 5
∴ 4th, 5th terms are middle terms.
∴ T4 = T3 + 1 = 7C3 (2x)7 – 3 (3y)3 = 7C3 24 33.x4.y3
T5 = T4 + 1 = 7C4(2x)7-4(3y)4 = 7C4. 23.34. x3. y4
Question 22.
n is a positive integer then prove that
Solution:
i) Co + C1 + C2 + …….. + Cn = 2n
ii) a) Co + C2 + C4 + … + Cn = 2n – 1 if n is even
(b) Co + C2 + C4 + …. + Cn – 1 = 2n – 1 if n is odd.
iii) (a) C1 + C3 + C5 + …. + Cn – 1 = 2n – 1 if n is even.
(b) C1 + C3 + C5 + …. + Cn – 1 = 2n – 1 if n is odd.
Solution:
We know (1 + x)n = nC0 + nC1 x + nC2 x2+ …… + nCn xn
= C0 + C1x + C2x2 + …… + Cnxn


![]()
Question 23.
Prove that C0 + 3.C1 + 5.C2 + ……… +(2n + 1). Cn = (2n + 2). 2n – 1.
Solution:
Let S = C0 + 3.C1 + 5.C2 + …… + (2n + 1). Cn —— (1)
By writing the terms in (1) in the reverse older, we get

Question 24.
Find the numerically greatest term in the binomial expansion of (1 – 5x)12 when x = \(\frac{2}{3}\).
Solution:
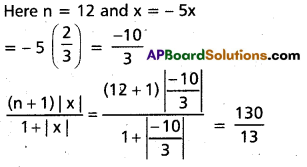
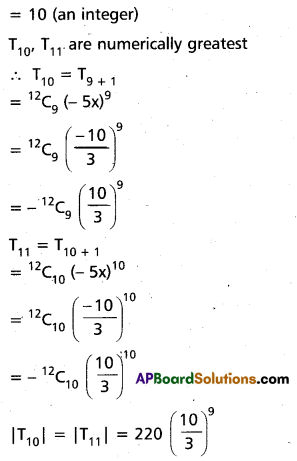
Question 25.
Compute numerically ireatist term (s) in the expansionly of (3x – 5y)n when x = \(\frac{3}{4}\), y = \(\frac{2}{7}\) and n = 17
Solution:
Given x = \(\frac{3}{4}\), y = \(\frac{2}{7}\) and n = 17

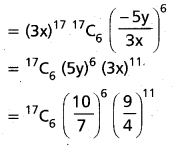
Question 26.
Find the largest binomial coefficients (s) in the expansion of
(i) (1 + x)19
(ii) (1 + x)24
Solution:
(i) Here n = 19 is an odd integer. Hence the largest binomial coefficients are
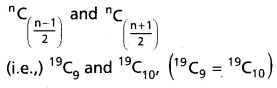
(ii) Here n = 24 is an even integer. Hence the largest binomial coefficient is
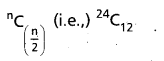
Question 27.
If 22Cr is the largest binomial coefficient in the expansion of (1 + x)22, find the value of 13Cr. (A.P. Mar’16, May ‘11)
Solution:
Here n = 22 is an even integer. There is only one largest binomial coefficient and it is
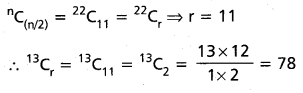
Question 28.
Find the 7th term in the expansion of \(\left(\frac{4}{x^{3}}+\frac{x^{2}}{2}\right)^{14}\)
Solution:
The general term in the expansion of

![]()
Question 29.
Find the 3rd term from the end in the expansion of \(\left(x^{-2 / 3}-\frac{3}{x^{2}}\right)^{8}\)
Solution:
Comparing with (X + a)n, we get
X = x-2/3, a = \(\frac{-3}{x^{2}}\), n = 8
In the given expansion \(\left(x^{-2 / 3}-\frac{3}{x^{2}}\right)^{8}\), we have n + 1 = 8 + 1 = 9 terms
Hence the 3rd term from the end is 7th term from the beginning.

Question 30.
Find the coefficient of x9 and x10 in the expansion of \(\left(2 x^{2}-\frac{1}{x}\right)^{2 c}\)
Solution:
If we write X = 2x2 and a = –\(\frac{1}{x}\), then the general term in the expansion of

Since r = \(\frac{31}{3}\) which is impossible since r must be a positive integer. Thus ‘there is no term containing x9 in the expansion of the given expression. In otherwords the coefficient of x9 is ‘0’.
Now, to find the coefficient of x10.
put 40 – 3r = 10
⇒ r = 10
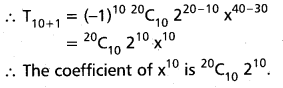
Question 31.
Find the term independent of x (that is the constant term) in the expansion of
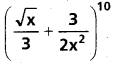
Solution:

Question 32.
If the coefficients of x10 in the expansion of \(\left(a x^{2}+\frac{1}{b x}\right)^{11}\) is equal to the coefficient of x-10 in the expansion of \(\left(a x-\frac{1}{b x^{2}}\right)^{11}\) ; find the relation between a and b where a and b are real numbers.
Solution:
The general term in the expansion of \(\left(a x^{2}+\frac{1}{b x}\right)^{11}\) is
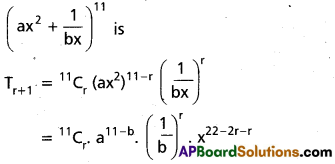
To find the coefficient of x10, put
22 – 3r = 10 ⇒ 3r = 12 ⇒ r = 4
Hence the coefficient of x10 in

Given that the coefficients are equal.
Hence from (1) and (2), we get
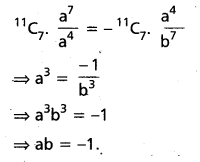
![]()
Question 33.
If the kth term is the middle term in the expansion of \(\left(x^{2}-\frac{1}{2 x}\right)^{20}\), find Tk and Tk + 3.
Solution:
The general term in the expansion of

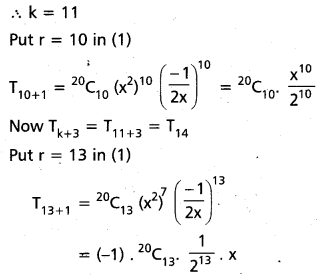
Question 34.
If the coefficients of (2r + 4)th and (r – 2)nd terms in the expansion of (1 + x)18 are equal, find r.
Solution:

Question 35.
Prove that 2.C0 + 7.C1 + 12.C2 + …… + (5n + 2)Cn = (5n + 4)2n – 1.
Solution:
First method:
The coefficients of C0, C1, C2, …., Cn are in A.P. with first term a = 2, C.d (d) = 5
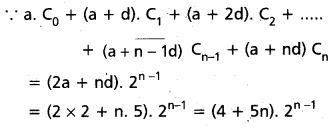
Second method:
General term in LH.S.

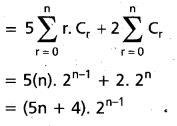
Question 36.
Prove that
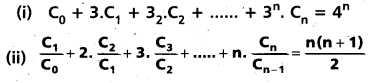
Solution:

![]()
Question 37.
For n = 0, 1, 2, 3 , n, prove that C0. Cr + C1. Cr + 1 + C2. Cr + 2 + ……. + Cn – r. Cn = 2nCn + 1. (T.S. Mar. ’15)
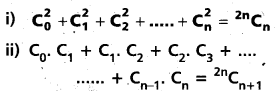
Solution:
We know that


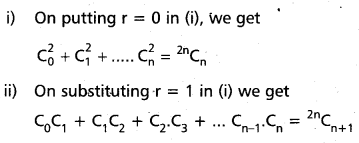
Question 38.
Prove that
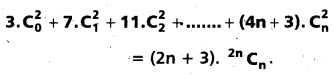
Solution:

Question 39.
Find the numerically greatest term (s) in the expansion of
i) (2 + 3x)10 when x = \(\frac{11}{8}\)
Solution:


ii) (3x – 4y)14 when x = 8, y = 3.
Solution:
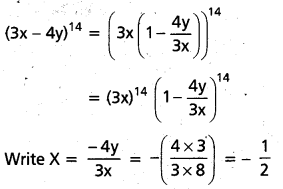
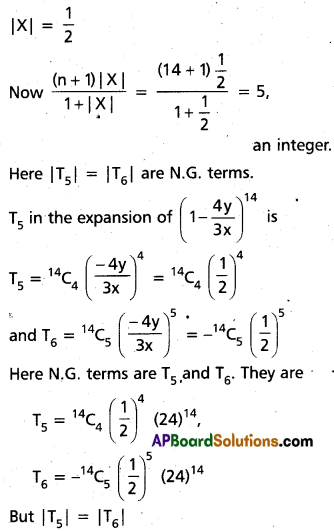
![]()
Question 40.
Prove that 62n – 35n – 1 is divisible by 1225 for all natural numbers of n.
Solution:
62n – 35n – 1 = (36)n – 35n – 1
= (35 + 1)n – 35n – 1

Hence 62n – 35n – 1 is divisible by 1225 for all integral values of n.
Question 41.
Suppose that n is a natural number and I, F are respectively the integral part and fractional part of (7 + \(\sqrt{3}\))n. Then show that
(i) I is an odd integer
(ii) (I + F) (I – F) = 1
Solution:
Given that (7 + 4\(\sqrt{3}\))n = I + F where I is an integer and 0 < F < 1

= 2k, where k is a positive integer —— (1)
Thus I + F + f is n even integer.
Since I is an integer, we get that F + f is an integer. Also since 0 < F < 1 and 0 < f < 1
⇒ 0 < F + f < 2
∵ F + 1 is an integer
We get F + f = 1
(i.e.,) I – F = f ——— (2)
(i) From (1) I + F + f = 2k
⇒ f = 2k – 1, an odd integer.
(ii) (I + F) (I – F) = (I + F) f
= (7 + 4\(\sqrt{3}\))n (7 – 4\(\sqrt{3}\))n
= (49 – 48)n = 1.
Question 42.
Find the coefficient of x6 in (3 + 2x + x2)6.
Solution:

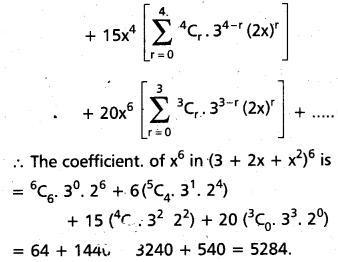
![]()
Question 43.
If n is a positive integer, then prove that
Co + \(\frac{C_{1}}{2}\) + \(\frac{C_{2}}{3}\) + ….. + \(\frac{C_{n}}{n+1}\) = \(\frac{2^{n+1}-1}{n+1}\)
Solution:

Question 44.
If n is a positive integer and x is any nonzero real number, then prove that
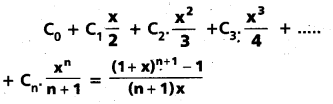
(May. ’14, May 13, ’05)
Solution:
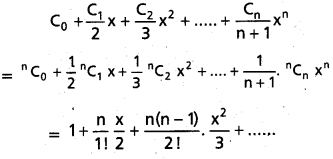

Question 45.
Prove that
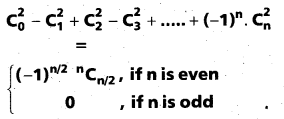
Solution:

Now we can find the term independent of in the L.H.S. of (1).
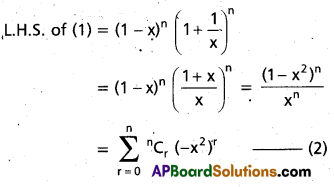
Suppose n is an even integer, say n = 2k. Then from (2),

When n is odd:
Observe that the expansion in the numerator of (2) contains only even powers of x.
∴ If n is odd, then there is no constant term in (2) (i.e.,) the term indep. of x in
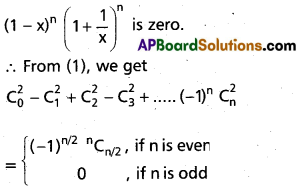
Question 46.
Find the set E of the value of x for which the binomial expansions for the following are valid
(i) (3 – 4x)3/4
(ii) (2 + 5)x-1/2
(iii) (7 – 4x)-5
(iv) (4 + 9x)-2/3
(iv) (a + bx)r (Mar. ’08)
Solution:
i) (3 – 4x)3/4 = 33/4\(\left(1-\frac{4 x}{3}\right)^{3 / 4}\)
The binomial expansion of (3 – 4x)3/4 is valid, when \(\frac{4 x}{3}\) < 1
i.e., |x| < \(\frac{3}{4}\)
i.e., E = \(\left(\frac{-3}{4}, \frac{3}{4}\right)\)
ii) (2 + 5x)-1/2 = 2-1/2\(\left(1+\frac{5 x}{2}\right)^{-1 / 2}\)
The binomial expansion of (2 + 5x)-1/2 is valid when |\(\frac{5 x}{3}\)| < 1 ⇒ |x| < \(\frac{2}{5}\)
i.e., E = (-\(\frac{2}{5}\), \(\frac{2}{5}\))
iii) (7 – 4x)-5 = 7-5\(\left(1-\frac{4 x}{7}\right)^{-5}\)
The binomial expansion of (7 – 4x)-5 is valid when \(\frac{4 x}{7}\) < 1 ⇒ |x| < \(\frac{7}{4}\)
i.e., E = \(\left(\frac{-7}{4}, \frac{7}{4}\right)\)
iv) (4 + 9x)-2/3 = 4-2/3 \(\left(1+\frac{9 x}{4}\right)^{-2 / 3}\)
The binomial expansipn of (4 + 9x)-2/3 is valid
When \(\frac{9 x}{4}\) < 1
⇒ |x| < \(\frac{4}{9}\)
⇒ x ∈ \(\left(\frac{-4}{9}, \frac{4}{9}\right)\)
i.e., E = \(\left(\frac{-4}{9}, \frac{4}{9}\right)\)
v) For any non zero reals a and b, the set of x for which the binomial expansion of (a + bx)r is valid when r ∉ Z+ ∪ {0}, is \(\left(-\frac{|a|}{|b|}, \frac{|a|}{|b|}\right)\)
![]()
Question 47.
Find the
(i) 9th term of \(\left(2+\frac{x}{3}\right)^{-5}\)
(ii) 10th term of \(\left(1-\frac{3 x}{4}\right)^{4 / 5}\)
(iii) 8th term of \(\left(1-\frac{5 x}{2}\right)^{-3 / 5}\)
(iv) 6th term of \(\left(3+\frac{2 x}{3}\right)^{3 / 2}\)
(i) 9th term of \(\left(2+\frac{x}{3}\right)^{-5}\)
Solution:
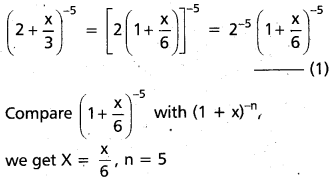
we get X = \(\frac{x}{6}\), n = 5
The general term in the binomial expansion of (1 + x)-n is

ii) 10th term of \(\left(1-\frac{3 x}{4}\right)^{4 / 5}\)
Solution:

iii) 8th term of \(\left(1-\frac{5 x}{2}\right)^{-3 / 5}\)
Solution:

iv) 6th term of \(\left(3+\frac{2 x}{3}\right)^{3 / 2}\)
Solution:

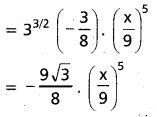
Question 48.
Write the first 3 terms in the expansion of
(i) \(\left(1+\frac{x}{2}\right)^{-5}\)
(ii) (3 + 4x)-2/3
(iii) (4 – 5x)-1/2
i) \(\left(1+\frac{x}{2}\right)^{-5}\)
Solution:
We have
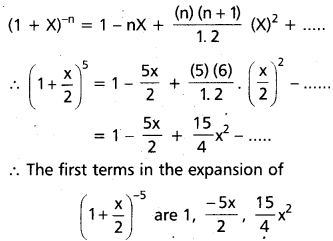
ii) (3 + 4x)-2/3
Solution:

![]()
iii) (4 – 5x)-1/2
Solution:
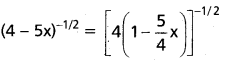
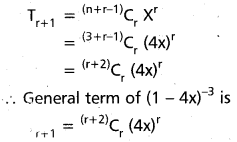
iv) (2 – 3x)-1/3
Solution:

Question 49.
Find the coefficient of x12 in \(\frac{1+3 x}{(1-4 x)^{4}}\)
Solution:

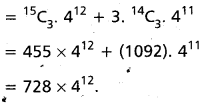
Question 50.
Find coeff. of x6 in the expansion of (1 – 3x)-2/5
Solution:

Question 51.
Find the sum of the infinite series
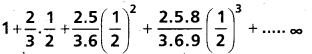
Solution:

![]()
Question 52.
Find the sum of the series
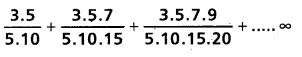
Solution:
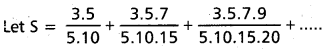

Question 53.
If x = \(\frac{1}{5}\) + \(\frac{1.3}{5.10}\) + \(\frac{1.3 .5}{5.10 .15}\) + ……. ∞ then find 3x2 + 6x. (Mar. ’14, ’07, ’06; May. ’11)
Solution:
Given that

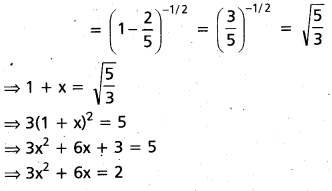
Question 54.
Find an approximate value of
i) \(\frac{1}{\sqrt[3]{999}}\)
ii) (627)1/4
Solution:


![]()
Question 55.
If |x| is so small that x3 and higher powers or x can be neglected, find approximate value of \(\frac{(4-7 x)^{1 / 2}}{(3+5 x)^{3}}\)
Solution:

Question 56.
Find an approximate value of \(\sqrt[6]{63}\) correct to 4 decimal places.
Solution:

Question 57.
If |x| is so small thát x2 and higher powers of x may be neglected, then find an approximate value of
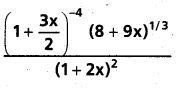
Solution:
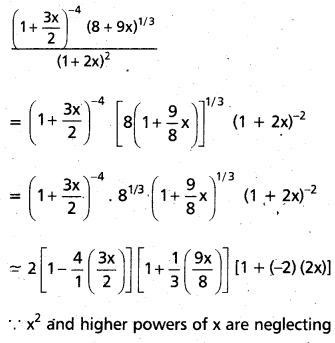

Question 58.
If |x| is so small that x4 and higher powers of x may be neglected, then find the approximate value of
\(\sqrt[4]{x^{2}+81}\) – \(\sqrt[4]{x^{2}+16}\)
Solution:
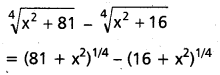

Question 59.
Suppose that x and y are positive and x is very small when compared to y. Then find an approximate value of
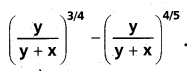
Solution:


![]()
Question 60.
Expand \(5 \sqrt{5}\) in increasing powers of \(\frac{4}{5}\)
Solution:
