Inter 1st Year Maths 1B Transformation of Axes Formulas

Use these Inter 1st Year Maths 1B Formulas PDF Chapter 2 Transformation of Axes to solve questions creatively.

Intermediate 1st Year Maths 1B Transformation of Axes Formulas

→ x = x’ + h ⇒ x’ = x – h

→ y = y’ + k ⇒ y’ = y – k

→ To make the first degree term absent, origin should be shifted to \(\left(\frac{h f-b g}{a b-h^{2}}, \frac{g h-a f}{a b-h^{2}}\right)\)

→ If the equation is ax² + by² + 2gx + 2fy + c = 0, origin should be shifted to be \(\left(-\frac{g}{a},-\frac{f}{b}\right)\)

	x’	y’
x	cos θ	– sin θ
y	sin θ	cos θ

x = x’ cos θ – y’ sin θ
x’ = x cos θ + y sin θ
y = x’ sin θ + y’ cos θ
y’ = – x sin θ + y cos θ

→ To make the xy term absent, axes should be rotated through an angle θ given by
tan 2θ = \(\frac{2 h}{a-b}\)

Rotation Of Axes (Change Of Direction):
I. Definition: If thc axes are rotated through an angle in the same plane by keeping the origin constant, then the transformation is called Rotation of axes.

2. Theorem: To find the co-ordinates of a point (x,y)are transformed to (X, Y)when the axes are rotated through an angle ‘6’ about the origin in the same plane.
Proof: Let x’Ox, yOY’ are the original axes
Let P(x,y)be the co-ordinates of the point in the above axes.
After rotating the axes through an angle ‘θ’, then the co-ordinates of P be (X, Y) w.r.t the new axes X’OX and YOY’ as in figure.

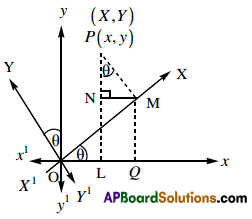
Since θ is the angle of rotation, then ∠xOA = ∠yOY = θ as in the figure.
Since L, M is projections of P on Ox and OX respectively. We can see that ∠LPM = ∠xOA = θ
Let N be the projection to PL from M
Now x = OL = OQ – LQ = OQ – NM
= OM cos θ – PM sin θ
= A cos θ – Y sin θ
y = PL = PN + NL = PN + MQ
PM cos θ + OM sin θ = Ycos θ + X sin θ
x = X cos θ – Y sin θ and
y = Y cos θ + X sin θ ………….(1)
Solving the above equations to get X and Y, then X = x cos θ + y sin θ and Y = -x sin θ + y cos θ ………… (2)

From (1) and (2) we can tabulate

	x’	y’
x	cos θ	– sin θ
y	sin θ	cos θ

Note:

• If the axes are turned through an angle ‘ θ ’, then the equation of a curve f (x, y) = 0 is transformed to f (X cos θ – Y sin θ, X sin θ + Y cos θ) = 0
• If f (X, Y) = 0is the transformed equation of a curve when the axes are rotated through an angle ‘ θ ’ then the original equation of the curve is f (x cos θ + y sin θ, – x sin θ + y cos θ) = 0

Theorem:
To find the angle of rotation of the axes to eliminate xy term in the equation ax² + 2hxy + by² + 2 gx + 2 fy + c = 0
Proof: given equation is ax²+ 2hxy + by² + 2 gx + 2 fy + c = 0
Since the axes are rotated through an angle θ, then x = X cos θ – Y sin θ, y = X sin θ + Y cos θ

Now the transformed equation is
a (X cos θ – Y sinθ)² + 2h (X cos θ – Y sin θ)(X sin θ + Y cos θ) + b (X sin θ + Y cos θ)² + 2g (X cos θ – Y sin θ) + 2 f (X sin θ + Y cos θ) + c = 0

⇒ X²cos²θ + Y²sin²θ – 2XYcosθsinθ) + 2h [X²cos θ + XY(cos²θ – sin²θ) – Y sin²θ cos²θ] + b[X² sin²θ + Y² cos²θ + 2XY cos θ sin θ) + 2g (X cos θ – Y sin θ) + 2 f (X sin θ + Y cos θ) + c = 0

Since XY term is to be eliminated, coefficient of XY = 0.
⇒ 2 (b – a) cos θ sin θ + 2h (cos2 θ – sin2 θ) = 0
⇒ h cos 2θ + (b – a) sin 2θ = 0
⇒ 2hcos2θ = (a -b)sin 2θ
⇒ Angle of rotation (θ) = \(\frac{1}{2}\) Tan^-1\(\left(\frac{2 h}{a-b}\right)\)
Note: The angle of rotation of the axes to eliminate xy term in
ax² + 2hxy + ay² + 2 gx + 2 fy + c = 0 is \(\frac{\pi}{4}\)

Translation of Axes:
1. Definition: Without changing the direction of the axes, the transformation in which the origin is shifted to another position or point is called translation of axes.

2. Theorem: To find the co-ordinates of a point (x, y) are translated by shifting the origin to a point (x, y)
Proof :

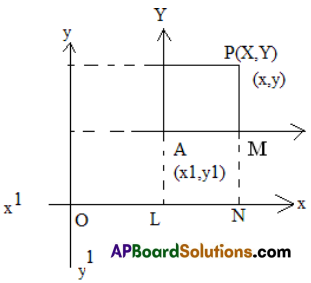
Let xox¹ xox¹, yoy¹ be the original axes and A(x₁, y₁) be a point to which the origin is shifted
Let AX, AY be the new axes which are parallel to the original axes as in figure.
Let P be any point in the plane whose coordinates w.r.t old system are (x, y)
And w.r.t new axes are (X, Y) .
From figure, A = (x₁, y₁) then AL = y₁, OL = x₁,
P(x, y )then x = ON = OL + LN = OL + AM = x₁ + X = X + x₁
Hence x = X + x₁.
y = PN = PM +MN = X+ AL = X + y₁
therefore, y = Y + y₁
hence x = X + x₁ y = Y + y₁

3. Theorem: To find the point to which the origin is to be shifted by translation of axes to eliminate x, y terms(first degree terms) in the equation ax² + 2xhy + by² + 2gx + 2fy + c = 0 (2 = ab)
Proof : given equation is ax2 + 2 xhy + by2 + 2gx + 2fy + c = 0
Let (x1, y1) be a point to which the origin is shifted by translation Let (X ,Y) be the new co-ordinates of the point (x, y) .
the equations of the transformation are x = X + x₁, y = Y + y₁
Now the transformed equation is
a (X + x₁)² + 2h (X + x₁)(Y + y₁)+ b (Y + y₁)² + 2g (X + x₁) + 2f [Y + y₁] + c = 0
⇒ a(X² + 2x₁X + x₁²) + 2h(XY + x₁Y + y₁X + x₁y₁) + b(Y² + 2y₁Y + y₁²) + 2g(X + x₁) + 2f (Y + y₁) + c = 0
⇒ aX² + 2hXY + bY² + 2X [ax₁ + hy₁ + g) + 2Y(hx₁ + by₁ + f ) + (ax₁² + 2x₁ + by₁² + 2gx₁ + 2fy₁ + c) = 0

Since x, y terms (the first degree terms) are to be eliminated
ax₁ + hy₁ + g = 0
hx₁ + by₁ + f = 0
Solving these two equations by the method of cross pollination

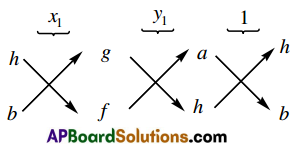
\(\frac{x_{1}}{h f-b g}=\frac{y_{1}}{g h-a f}=\frac{1}{a b-h^{2}}\) ⇒ x₁ = \(\frac{h f-b g}{a b-h^{2}}\) y₁ = \(\frac{g h-a f}{a b-h^{2}}\)
New Origin is ⇒ (x₁, y₁) = \(\left(\frac{h f-b g}{a b-h^{2}}, \frac{g h-a f}{a b-h^{2}}\right)\)

Note:
(i) The point to which the origin has to be shifted to eliminate x, y terms by translation in the equation ax2 + by2 + 2gx + 2 fy + c = 0is \(\left(\frac{-g}{a}, \frac{-f}{b}\right)\)
If b = a, then the new origin is \(\left(\frac{-g}{a}, \frac{-f}{b}\right)\)

(ii) The point to which the origin has to be shifted to eliminate x, y terms by translation of axes in the equation a(x + x₁)² + b(y + y₁)² = c is (-x₁, – y₁)

(iii) The point to which the origin has to be shifted to eliminate x, y terms by translation in the equation 2hxy + 2gx + 2 fy + c = 0 is \(\left(\frac{-f}{h}, \frac{-g}{h}\right)\)
l h ’ h I
Theorem : To find the condition that the equation ax² + 2hxy + by² + 2 gx + 2 fy + c = 0 to be in the form aX² + 2hXY + bY² = 0 when the axes are translated. (h² ≠ ab)
Proof : From theorem 3, we get
ax₁ + hy₁ + g = 0 ………..(1)
hx₁ + by₁ + f = 0 …………(2)

Solving (1) and (2),
(x₁, y₁) = \(\left(\frac{h f-b g}{a b-h^{2}}, \frac{g f-a f}{a b-h^{2}}\right)\)

Since the equation is to be in the form of aX² + 2hXY + bY² = 0 ,then for this we should have axj² + 2hx₁y₁ + by² + 2 gx₁ + 2 fy₁ + c = 0
⇒ (ax₁ + hyx + g) x₁ + (x₁ + byx + f) yx + (gx + fy₁ + c ) = 0
⇒ (0).x + (0), y + (gx₁ + fyx + c) = 0 from(1) and (2) ⇒ gx₁ + fyx + c = 0 …………..(3)

Substituting x₁, y₁ in (3), we get
g\(\left(\frac{h f-b g}{a b-h^{2}}\right)\) + f\(\left(\frac{g h-a f}{a b-h^{2}}\right)\) + c = 0
⇒ fgh – bg² + fgh – af² + abc + -ch² = 0
⇒ abc + 2 fgh – af² – bg² – ch² = 0