Inter 1st Year Maths 1B The Straight Line Solutions Ex 3(a)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B The Straight Line Solutions Exercise 3(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B The Straight Line Solutions Exercise 3(a)

I.

Question 1.
Find the slope of the line x + y = 0 and x – y = 0.
Solution:
Slope of x + y = 0 is – \(\frac{a}{b}\) = -1
Slope of x – y = 0 is 1

Question 2.
Find the equation of the line containing the points (2, -3) and (0, -3).
Solution:
Equation of the line is
(y – y₁) (x₁ – x₂) = (x – x₁) (y₁ – y₂)
(y + 3)(2 – 0) = (x – 2)(-3 + 3)
2(y + 3) = 0
⇒ y + 3 = 0

Question 3.
Find the equation of the line containing the points (1, 2) and (1, -2).
Solution:
Equation of the line is
(y – y₁) (x₁ – x₂) = (x – x₁) (y₁ – y₂)
(y – 2)(1 – 1) = (x – 1) (2 + 2)
0 = 4(x – 1) ⇒ x – 1 =0

Question 4.
Find the angle which the straight line y = √3x – 4 makes with the Y-axis.
Solution:
Equation of the line is y = √3x – 4
Slope = m = √3 = tan \(\frac{\pi}{6}\)
Angle made with X-axis = \(\frac{\pi}{6}\)
Angle made with Y – axis = \(\frac{\pi}{2}-\frac{\pi}{6}=\frac{\pi}{3}\)

Question 5.
Write the equation of the reflection of the line x = 1 in the Y-axis.
Solution:

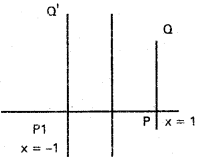
Equation of PQ is x = 1
Reflection about Y – axis is x = – 1
i.e., x + 1 = 0

Question 6.
Find the condition for the points (a, 0), (h, k) and (0, b) when ab ≠ 0 to be collinear.
Solution:
A(a, 0), B(h, k), C(0, b) are collinear.
⇒ Slope of AB = Slope of AC
\(\frac{k-0}{h-a}=\frac{-b}{a}\)
ak = -bh + ab
bh + ak = ab
\(\frac{h}{a}+\frac{k}{b}=1\)

Question 7.
Write the equations of the straight lines parallel to X-axis is
i) at a distance of 3 units above the X-axis and ii)at a distance of 4 units below the X-axis.
Solution:
I)

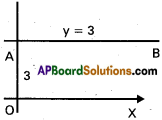
Equation of the required line AB is y = 3

ii)

Equation of A’B’ is y = — 4 ; y + 4 = 0

8. Write the equations of the straight line parallel to Y – axis and
i) at a distance of 2 units from the Y-axis to the right of it.
ii) at a distance of 5 units from the Y-axis to the left of it.
Solution:
i)

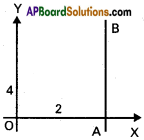
Equation of the required line AB is x = 2

ii)

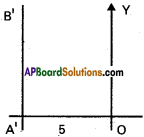
Equation of the required line A’B’
x = -5
x + 5 = 0

II.

Question 1.
Find the slopes of the straight line passing through the following pairs of points.
i) (-3, 8) (10, 5)
ii) (3, 4) (7, -6)
iii) (8,1), (-1, 7)
iv) (-P, q) (q, -p) (pq ≠ 0)
Solution:

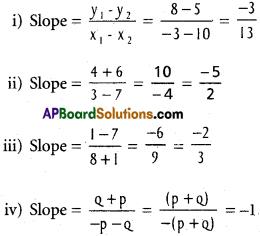
Question 2.
Find the value of x, if the slope of the line passing through (2, 5) and (x, 3) is 2.
Solution:
Slope = \(\frac{y_{1}-y_{2}}{x_{1}-x_{2}}=\frac{5-3}{2-x}=2\)
2 = 2(2 – x)
x = 2 – 1 = 1

Question 3.
Find the value of y if the line joining the points (3, y) and (2, 7) is parallel to the line joining the points (-1, 4) and (0,6).
Solution:
A(3, y), B(2, 7), P(-1, 4) and Q(0, 6) are the given points.
m₁ = Slope of AB = \(\frac{y-7}{3-2}\) = y – 7
m₂ = Slope of PQ = \(\frac{4-6}{-1-0}=\frac{-2}{-1}=2\)

AB and PQ are parallel
m₁ = m₂ ⇒ y – 7 = 2
y = 2 + 7 = 9

Question 4.
Find the slopes of the lines i) parallel to and ii) perpendicular to the line passing through (6, 3) and (- 4,5).
Solution:
A(6, 3) and B(-4, 5) are the given points.
m = Slope of AB = \(\frac{3-5}{6+4}=\frac{-2}{10}=-\frac{1}{5}\)

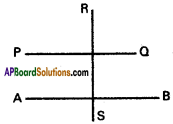
PQ is parallel to AB
(i) Slope of PQ = m = – \(\frac{1}{5}\)
RS is perpendicular to AB

(ii)Slope of RS = – \(\frac{1}{m}\) =5 m

Question 5.
Find the equation of the straight line which makes the following angles with the positive X-axis in the positive direction and which pass through the points given below
i) \(\frac{\pi}{4}\) and (0,0)
ii) \(\frac{\pi}{3}\) and(1, 2)
iii) 135° and (3, -2)
iv) 150° and (-2, -1)
Solution:
i) m = Slope = tan 45° = 1
Equation of the line is y – y₁ = m(x – x₁)
y – 0 = 1(x – 0)
i.e., y = x
or x – y = 0

ii) m = tan 60° – √3
Equation of the line is
y – 2 = √3 (x – 1)
= √3x – √3
√3x – y+(2 – √3) = 0

iii) m = tan 135° = tan (180° -45°)
= – tan 45° = -1
Equation of the line is y + 2 = -1(x – 3)
= – x + 3
i.e., x + y – 1 = 0

iv) m = tan 150° = tan (180° – 30°)
= – tan 30° = – \(\frac{1}{\sqrt{3}}\)
Equation of the line is
y + 1 = – \(\frac{1}{\sqrt{3}}\) (x + 2)
√3y + √3 = – x – 2
x + √3y + (2 + √3) = 0

Question 6.
Find the equations of the straight lines passing through the origin and making equal angles with the co-ordinate axes.
Solution:
Case (i) : PP1 makes an angle 45° with positive X-axis
m = tan 45° = 1
PP’ passes through 0(0, 0)
Equation of PP’ is y – 0 = 1 (x – 0)

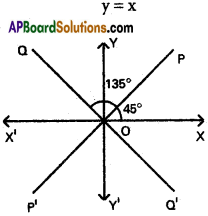
Case ii) : QQ’ makes an angle 135° with positive X-axis
m = tan 135° = tan (180° – 45°) = -tan 45°
Equation of QQ’ is y – 0 = -1 (x – 0)
y = -x

Question 7.
The angle made by a straight line with the positive X-axis in the positive direction and the Y-intercept cut off by it are given below. Find the equation of the straight line.
i) 60°, 3
ii) 150°, 2
iii) 45°, -2
iv) Tan^-1(\(\frac{2}{3}\)), 3
Solution:
i) Equation of the line is y = mx + c
m = tan 60° = √3, c = 3
Equation of the line is y = √3x + 3
√3x – y + 3 = 0

ii) m = tan 150° = tan (180°-30°)
= – tan 30° = \(\frac{-1}{\sqrt{3}}\), c = 2
Equation of the line is y =- \(\frac{1}{\sqrt{3}}\)x + 2
√3 y = -x + 2 √3x
x + √3y – 2 – √3 =0

iii) m = tan 45° = 1
c = -2
Equation of the line is
y = x – 2
x – y – 2=0

iv) θ = tan^-1(\(\frac{2}{3}\)) ⇒ m = tan θ = \(\frac{2}{3}\),c = 3
Equatidn of the line is y = \(\frac{2}{3}\) x + 3
3y = 2x + 9
2x – 3y + 9 = 0

Question 8.
Find the equation of the straight line passing through (-4, 5) and cutting off equal and non-zero intercepts on the coordinate axes.
Solution:
Equation of the line in the intercept form is
\(\frac{x}{a}+\frac{y}{b}\) = 1
Given a = b
Equation of the line is \(\frac{x}{a}+\frac{y}{b}\) = 1
⇒ x + y = a
This line passes through P(- 4, 5)
-4 + 5 = a ⇒ a = 1
Equation of the required line is x + y = 1 or x + y – 1 = 0

Question 9.
Find the equation of the straight line passing through (-2, 4) and making non¬zero intercepts whose sum is zero.
Solution:
Equation of the line in the intercept form is
\(\frac{x}{a}+\frac{y}{b}\) = 1
Given a + b = 0 ⇒ b = -a
Equation of the line is \(\frac{x}{a}-\frac{y}{b}\)
⇒ x – y = a
This line passes through P(-2,4)
∴ -2 – 4 = a ⇒ a = -6
Equation of the required line is x – y = -6
⇒ x – y + 6 = 0

III.

Question 1.
Find the equation of the straight line passing through the point (3, -4) and making X and Y-intercepts which are in the ratio 2 : 3.
Solution:
Equation of the line in the intercept form is x y
\(\frac{x}{a}+\frac{y}{b}\) = 1
Given \(\frac{a}{b}\) = \(\frac{2}{3}\) ⇒ b = \(\frac{3a}{2}\)
Equation of the line is \(\frac{x}{a}+\frac{2 y}{3 a}=1\)
⇒ 3x + 2y = 3a
This line passes through P(3, – 4)
9 – 8 = 3a ⇒ 3a = 1

Equation of the required line is 3x + 2y = 1
⇒ 3x + 2y – 1 = 0

Question 2.
Find the equation of the straight line passing through the point (4, -3) and perpendicular to the line passing through the points (1, 1) and (2, 3).
Solution:
A(1, 1), B(2, 3) are the given points.
m = Slope of AB = \(\frac{1-3}{1-2}=\frac{-2}{-1}=2\)

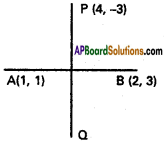
PQ is perpendicular to AB
Slope of PQ = –\(\frac{1}{m}\) = – \(\frac{1}{2}\)
PQ passes through P(4, -3)
Equation of PQ is y – y₁ = m(x – x₁)
y + 3 = –\(\frac{1}{2}\)(x – 4)
2y + 6 = -x + 4 ⇒ x + 2y + 2 = 0

Question 3.
Show that the following sets of points are collinear and find the equation of the line L containing them.
i) (-5, 1), (5, 5), (10, 7)
ii) (1, 3), (-2, – 6), (2, 6)
iii) (a, b + c), (b, c + a), (c, a + b)
Solution:
i) A(-5, 1), B(5, 5), C(10, 7) are the given points.
Equation of AB is
(y – y₁) (x₁ – x₂) = (x – x₁) (y₁ – y₂)
(y- 1) (-5 – 5) = (x + 5) (1 – 5)
– 10y + 10 = -4x – 20
4x – 10y + 30 = 0
or 2x – 5y + 15 = 0

C(10, 7)
2x – 5y + 15 = 2.10 – 5.7 + 15
= 20 – 35 + 15 = 0

A, B, C are collinear.
Equation of the line containing them is 2x – 5y + 15 = 0

ii) A(1, 3), B(-2, -6), C(2, 6)
Equation of AB is
(y – 3) (1 + 2) = (x – 1) (3 + 6)
3(y – 3) = 9(x – 1)
y – 3 = 3x – 3
3x – y = 0

C(2, 6)
3x – y = 3.2 – 6 = 6 – 6 = 0

∴ The given points A, B, C are collinear.
Equation of the line containing A,B,C is 3x – y = 0

iii) A(a, b f c), B(b, c + a), C(c, a + b)
Equation of AB is
(y – (b + c)) (a-b) = (x – a)(b + c – c – a)
(y – b – c) (a – b) = -(a – b) (x – a)
y – b – c = -x + a
or x + y – (a + b + c) = 0
C (c, a + b)
c + a + b – a – b – c = 0
C lies on AB
A, B, C are collinear.
Equation of the line containing them is x + y = a + b + c

Question 4.
A(10, 4), B(-4, 9) and C(-2, -1) are the vertices of a triangle. Find the equations of
i) \(\stackrel{\leftrightarrow}{A B}\)
ii) the median through A
iii) the altitude through B
iv) the perpendicular bisector the side of \(\stackrel{\leftrightarrow}{A B}\)
Solution:
i) A(10,4), B(-4, 9) are the given points.
Equation of AB is
(y – 4) (10 + 4) = (x – 10) (4 – 9)
14y – 56 = -5x + 50
5x + 14y – 106 = 0

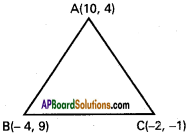
ii) D is the mid-point of BC

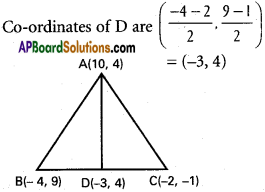
A (10,4) is the other vertex Equation of AD is
(y – 4) (10 + 3) = (x + 3) (4 – 4)
13(y – 4) = 0 ⇒ y – 4 = 0 (or) y = 4

iii)

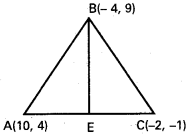
Slope of AC = \(\frac{4+1}{10+2}=\frac{5}{12}\)
BE is perpendicular to AC
Slope of BE = \(\frac{-1}{m}=\frac{-12}{5}\)

BE passes through B(-4, 9)
Equation of the altitude BE is
y – 9 = \(\frac{-12}{5}\)(x + 4)
5y – 45 = -12x – 48
12x + 5y + 3 = 0

iv) O is the mid-point of AB