Students get through Maths 1B Important Questions Inter 1st Year Maths 1B Pair of Straight Lines Important Questions which are most likely to be asked in the exam.
Intermediate 1st Year Maths 1B Pair of Straight Lines Important Questions
Question 1.
Does the equation x2 + xy + y2 = 0 represent a pair of lines?
Solution:
a = 1, b = 1, h = \(\frac{1}{2}\), ⇒ h2 = \(\frac{1}{4}\), ab = 1
h2 = ab < 0 i.e., h2 < ab.
∴ The given equation does not represent a pair of lines
![]()
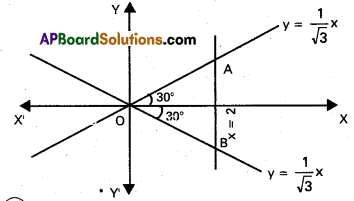
Question 2.
Find the nature of the triangle of formed by the lines x2 – 3y2 = 0 and x = 2.
Solution:
Combined equation of OA and OB is
x2 – 3y2 = 0
(x + \(\sqrt{3}\) y) (x – \(\sqrt{3}\) y) = 0
x + \(\sqrt{3}\) y = 0 and x – \(\sqrt{3}\) y = 0
i.e., y = \(\frac{1}{\sqrt{3}}\) x, y = –\(\frac{1}{\sqrt{3}}\) x are equally inclined to the X—axis, the inclination being 30°
∴ ∠OAB – ∠OBA = 60°
∴ The triangle is equilateral
Question 3.
Find the centroid of the triangle formed by the lines 12x2 – 20xy + 7y2 = 0 and 2x – 3y + 4 = 0.
Solution:
Combined equation of OA and OB is
12x2 – 20xy + 7y2 = 0 ………………….. (1)
Equation of AB is 2x – 3y + 4 = 0
2x = 3y – 4
Substituted in (1)
3(3y – 4)2 – 1oy (3y – 4) + 7y2 = 0
3(9y2 + 16 – 24y) – 30y2 + 40y + 7y2 = 0
27y2 +48 – 72y – 30y2 + 40y + 7y2 = 0
4y2 – 32y + 48 = 0
y2 – 8y + 12 = 0
(y – 2) (y – 6) = 0 ⇒ y = 2 or 6
x = \(\frac{3 y-4}{2}\)
y = 2 ⇒ x = \(\frac{6-4}{2}\) = 1
y = 6 ⇒ x = \(\frac{18-4}{2}\) = 7
7 2
∴ Vertices and O (0, 0), A (1, 2), B( 7, 6)
Centroid of OAB is
(\(\frac{0+1+7}{3}\), \(\frac{0+2+6}{3}\)) = (\(\frac{8}{3}\), \(\frac{8}{3}\))
![]()
Question 4.
Prove that the lines represented by the equations x2 – 4xy + y2 = 0 and x + y = 3 form an equilateral triangle.
Solution:
Since the straight line L: x + y = 3 makes 45° with the negative direction of the X-axis, none of the lines which makes 60° with the line L is vertical. If ‘m’ is the slope of one such straight line, then
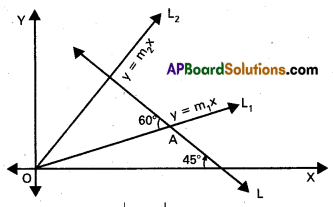
\(\sqrt{3}\) = tan 60° = \(\left|\frac{m+1}{1-m}\right|\) and so, m satisfies the equation (m + 1)2 = 3(m – 1)2
(or) m2 – 4m + 1 = 0 …………………….. (1)
But the straight line having slope’m1 and passing through the origin is
y = mx ……………………. (2)
So the equation of the pair of lines passing through the origin and inclined at 60° with the line L is obtained by eliminating’m’ from the equations (1) and (2). Therefore the combined equation of this pair of lines is
(\(\frac{y}{x}\))2 – 4(\(\frac{y}{x}\)) + 1 = 0 (i.e.,) x2 – 4xy + y2 = 0
Which is the same as the given pair of lines. Hence, the given triad of lines form an equilateral triangle.
Question 5.
Show that the product of the perpendicular distances from a point (α, β) to the pair of straight lines ax2 + 2hxy + by2 = 0 is \(\frac{\left|a \alpha^{2}+2 h \alpha \beta+b \beta^{2}\right|}{\sqrt{(a-b)^{2}+4 h^{2}}}\). [May 11, 07; Mar. 07, 04]
Solution:
Let ax2 + 2hxy + by2 = (l1x + m1y) (l2x + m2y)
Then the separate equations of the lines represented by the equation
ax2 + 2hxy + by2 = 0 are
L1 : l1x + m1y = 0 and L2 : l1x + m1y = 0
Also, we have l1l2 = a; m1m2 = b and
l1m2 + l2m1 = 2h
d1 = length of the perpendicular from (α, β) to L1 = \(\frac{\left|l_{1} \alpha+\mathrm{m}_{1} \beta\right|}{\sqrt{l_{1}^{2}+\mathrm{m}_{1}^{2}}}\)
d2 = length of the perpendicular from (α, β) to L2 = \(\frac{\left|l_{2} \alpha+m_{2} \beta\right|}{\sqrt{l_{2}^{2}+m_{2}^{2}}}\)
Then, the product of the lengths of the perpendiculars from (α, β) to the given pair of lines = d1d2
= \(\frac{\left\|\left(l_{1} \alpha+m_{1} \beta\right)\left(l_{2} \alpha+m_{2} \beta\right)\right\|}{\sqrt{\left(l_{1}^{2}+m_{1}^{2}\right)\left(l_{2}^{2}+m_{2}^{2}\right)}}\)
= \(=\frac{\left|a \alpha^{2}+2 h \alpha \beta+b \beta^{2}\right|}{\sqrt{(a-b)^{2}+4 h^{2}}}\)
![]()
Question 6.
Let ax2 + 2hxy + by2 = 0 represent a pair of straight lines. Then show that the equation of the pair of straight lines.
i) Passing through (x0, y0) and parallel to the given pair of lines is
a(x – x0)2 + 2h(x – x0) (y – y0) + b(y – y0)2 = 0 and
ii) Passing through (x0, y0) and perpendicular to the given pair of lines is
b(x – x0)2 – 2h(x – x0) (y – y0) + a(y – y0)2 = 0
Solution:
Let ax2 + 2hxy + by2 = (l1x + m1y) (l2x + m2y).
Then the lines L1 and L2 are represented by the given equation are respectively
l1x + m1y = 0 and l2x + m2y = 0.
Also we have l1l2 = a, m1m2 = b and
l1m2 + l2m1 = 2h
(i) The straight lines passing through (x0, y0) and parallel to L1 and L2 are respectively
l1x + m1y = l1x0 + m1y0 (or)
l1(x – x0) + m1(y – y0) = 0 and
l2(x -x0) + m2(y – y0) = 0.
Therefore, their combined equation is
[l1(x – x0) + m1(y – y0)] [l2(x – x0)+ m2(y – y0)] = 0
(or) a(x – x0)2 + 2h(x – x0) (y – y0) + b(y – y0)2 = 0
(ii) The straight lines passing through (x0, y0) and perpendicular to the pair L1 and L2 are respectively.
m1x – l1y = m1x0 – l1y0 (or)
m1(x – x0) – l1(y – y0) = 0 and
m2(x – x0) – l2(y – y0) = 0.
Hence their combined equation is
[m1(x – x0) – l1(y – y0)] [m2(x – x0) – l2(y – y0)] = 0
(i.e.,) b(x – x0)2 – 2h(x – x0) (y – y0) + a(y – y0)2 = 0
[Note : The pair of lines passing through the origin and perpendicular to the pair of lines given by ax2 + 2hxy + by2 = 0 is bx2 – 2hxy + ay2 = 0].
![]()
Question 7.
Show that the area of the triangle formed by the lines ax2 + 2hxy + by2 = 0 and lx + my + n = 0 is \(\left|\frac{n^{2} \sqrt{h^{2}-a b}}{a m^{2}-2 h / m+b l^{2}}\right|\)
Solution:
Let \(\overleftrightarrow{\mathrm{OA}}\) and \(\overleftrightarrow{\mathrm{OB}}\) be the pair of straight lines represented by the equation
ax2 + 2hxy + by2 = 0 (see figure) and \(\overleftrightarrow{\mathrm{AB}}\) be the line lx + my + n = 0
Let ax2 + 2hxy + by2 = (l1x + m1y) (l2x + m2y) and\(\overleftrightarrow{\mathrm{OA}}\) and \(\overleftrightarrow{\mathrm{OB}}\) be the lines.
l1x + m1y = 0 and l2x + m2y = 0 respectively.
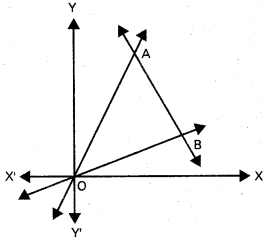
Let A = (x1, y1) and B = (x2, y2).
Then l1x1 + m1y1 = 0 and l1x1 + m1y1 + n = 0.
So, by the rule of cross-multiplication, we obtain

Question 8.
Two equal sides of an isosceles triangle are 7x – y + 3 = 0 and x + y – 3 = 0 and its third side passes through the point (1,0). Find the equation of the third side.
Solution:
Let the lines 7x – y + 3 – 0 and x + y – 3 = 0 intersect at A. If we draw lines (not passing through A) perpendicular to each of the bisectors of the angles at A, we get isosceles triangles, equal sides being along the given lines.
(∆ABF ≅ ∆AFC and ∆ADG ≅ ∆AGE)
Of them, we require those triangles whose third sides pass through (1, 0).
The equations of the bisectors of the angles between 7x – y + 3 = 0 and x + y – 3 = 0 are
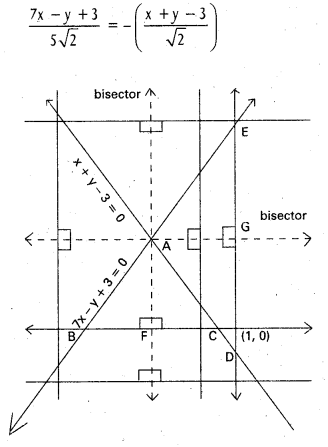
⇒ 7x – y + 3 = ± 5(x + y – 3)
⇒ x – 3y + 9 = 0 and 3x + y – 3 = 0.
The third sides will be those lines perpendicular to the bisectors and intersecting at (1, 0).
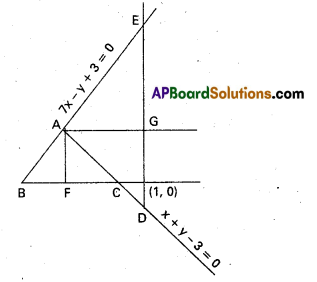
The side perpendicular to x – 3y + 9 = 0 and passing through (1, 0) is 3x + y – 3 =0. The other one is (x – 1) -3(y – 0) = 0 i.e., x – 3y – 1 = 0. Therefore 3x + y- 3 = 0 and x- 3y— 1 = 0 are the required ones. [In the Figure ∆ABC and ∆ADE are isosceles with \(\overline{B C}\) and \(\overline{D E}\) as third sides].
Question 9.
Find the angle between the straight lines represented by 2x2 + 5xy + 2y2 – 5x – 7y + 3 = 0.
Solution:
a = 2, b = 2, h = \(\frac{5}{2}\)
cos θ = \(\frac{|a+b|}{\sqrt{(a-b)^{2}+4 h^{2}}}=\frac{|2+2|}{\sqrt{(2-2)^{2}+4 \cdot \frac{25}{4}}}\) = \(\frac{4}{5}\)
θ = cos-1 (\(\frac{4}{5}\))
Question 10.
Find the equation of the pair of lines passing through the origin and parallel to the pair of lines 2x2 + 3xy – 2y2 – 5x + 5y – 3 = 0
Solution:
Equation of the given pair of lines is
2x2 + 3xy – 2y2 – 5x + 5y – 3 = 0
Equation of the pair of parallel lines passing through the origin is ax2 + 2hxy + by2 = 0 is 2x2 + 3xy – 2y2 = 0
![]()
Question 11.
Find the equation of the pair of lines passing through the origin and perpendicular to the pair of lines ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
Solution:
Equation to the pair of lines parallel to the given lines and passing through the origin is ax2 + 2hxy + by2 = 0
Equation of the pair of lines perpendicular to the given lines and passing through the origin is bx2 – 2hxy + ay2 = 0
Question 12.
If x2 + xy – 2y2 + 4x – y + k = 0 represents a pair of straight lines, find k.
Solution:
a = 1, b = -2, c = k; f = –\(\frac{1}{2}\), g = 2, h = \(\frac{1}{2}\)
The condition is
abc + 2fgh – af2 – bg2 – ch2 = 0
2k + 2(-\(\frac{1}{2}\)) . 2\(\frac{1}{2}\) – 1.\(\frac{1}{4}\) + 2.\(\frac{4}{a}\) – k\(\frac{1}{4}\) = 0
-8k – 4 – 1 + 8 – k = 0
9k = 27 ⇒ k = 3
Question 13.
Prove that the equation 2x2 + xy – 6y2 + 7y – 2 = 0 represents a pair of straight lines.
Solution:
a = 2
b = -6
c = -2
f = \(\frac{7}{2}\)
g = 0
h = \(\frac{1}{2}\)
abc + 2fgh – af2 – bg2 – ch2
= 2(-6) (-2) + 2.\(\frac{7}{2}\) 0\(\frac{1}{2}\) – 2(\(\frac{7}{2}\))2 + 6.0 + 2.(\(\frac{1}{2}\))2
= 24 – \(\frac{49}{2}\) + \(\frac{1}{2}\) = 0
h2 – ab = \(\frac{1}{4}\) + 12 > 0,
g2 – ac = 0 + 4 = 4 > 0
f2 – bc = \(\frac{49}{4}\) – 12 = \(\frac{1}{4}\) > 0
The given equation represents a pair of line.
![]()
Question 14.
Prove that the equation 2x2 + 3xy – 2y2 – x + 3y – 1 = 0 represents a pair of perpendicular straight lines.
Solution:
a = 2
b = -2
c = -1
f = \(\frac{3}{2}\)
g = –\(\frac{1}{2}\)
h = \(\frac{3}{2}\)
abc + 2fgh – af2 – bg2 – ch2
= 2(-2) (-1) + 2.\(\frac{3}{2}\) (-\(\frac{1}{2}\)).\(\frac{3}{2}\) – 2(\(\frac{9}{4}\)) + 2.\(\frac{1}{4}\) + \(\frac{1.9}{2}\)
= 4.-\(\frac{9}{4}\) – 2.\(\frac{9}{4}\) + \(\frac{1}{2}\) + \(\frac{9}{4}\)
= \(\frac{9}{2}\) – \(\frac{9}{2}\) = 0
h2 – ab = \(\frac{9}{4}\) + 4 = \(\frac{25}{4}\) > 0,
g2 – ac = \(\frac{1}{4}\) + 2 > 0
f2 – bc = \(\frac{9}{4}\) – 2 = \(\frac{1}{4}\) > 0
a + b = 2 – 2 = 0
The given equation represents a pair of perpendicular line.
Question 15.
Show that the equation 2x2 – 13xy – 7y2 + x + 23y – 6 = 0 represents a pair of straight lines. Also find the angle between them and the co-ordinates of the point of intersection of the lines.
Solution:
Here a = 2
b = -7
c = -6
f = \(\frac{23}{2}\)
g = \(\frac{1}{2}\)
h = –\(\frac{13}{2}\)
abc + 2fgh – af2 – bg2 – ch2
= 2(-7) (-6) + 2.\(\frac{23}{2}\) . \(\frac{23}{2}\) . (-\(\frac{13}{2}\)) – 2\(\frac{529}{4}\) + 7.\(\frac{1}{4}\) + 6 . \(\frac{169}{4}\)
= \(\frac{1}{4}\) (336 – 299 – 1058 + 7 + 1014)
= \(\frac{1}{4}\) (1357 – 1357) = 0
h2 – ab = \(\frac{169}{4}\) + 14 > 0,
g2 – ac = \(\frac{1}{4}\) + 12 > 0,
f2 – bc = \(\frac{529}{4}\) – 42 > 0
The given equation represents a pair of lines

= \(\frac{-13-92}{-56-169}\) = \(\frac{-105}{-225}\) = \(\frac{7}{15}\)
Point of intersection is P (\(\frac{19}{15}\), \(\frac{7}{15}\))
Question 16.
Find that value of λ for which the equation λx2 – 10xy + 12y2 + 5x – 16y -3 = 0 represents a pair of straight lines.
Solution:
Here a = λ
b = 12
c = -3
f = -8
g = \(\frac{5}{2}\)
h = -5
The given equation represents a pair of lines
abc + 2fgh – af2 – bg2 – ch2 = 0
-36λ + 2(-8)\(\frac{5}{2}\) (-5) – λ . 64 – 12 . \(\frac{25}{4}\) + 3 . 25 = 0
-36λ + 200 – 64λ – 75 + 75 = 0
100λ = 200
⇒ λ = 2 ⇒ a = 2
h2 – ab = 25 – 24 = 1 > 0
f2 – bc = 64 + 36 = 100 > 0
g2 – ac = \(\frac{25}{4}\) + 6 = \(\frac{49}{4}\) > 0
∴ The given equation represents a pair of lines for λ = 2.
![]()
Question 17.
Show that die pairs of straight lines 6x2 – 5xy – 6y2 = 0 and 6x2 – 5xy – 6y2 + x + 5y – 1 = 0 form a square.
Solution:
H ≅ 6x2 – 5xy – 6y2 = (3x + 2y) (2x – 3y)
and S ≅ 6x2 – 5xy – 6y2 + x + 5y – 1
= (3x + 2y- 1) (2x – 3y + 1).
∴ H = 0 represents the lines 3x + 2y = 0 and 2x – 3y = 0 which are perpendicular and S = 0 represents the lines 3x + 2y – 1 = 0, 2x – 3y + 1 = 0 which are also perpendicular. These two pairs of perpendicular lines, therefore, determine a rectangle.
Also the distance between the pair of opposite sides 3x + 2y = 0 and 3x + 2y – 1 = 0 is \(\frac{1}{\sqrt{13}}\) and this is the same as the distance between the other pair of opposite sides 2x – 3y = 0 and 2x – 3y + 1 = 0 of the rectangle. Hence the rectangle is a square.
Question 18.
Show that the equation 8x2 – 24xy + 18y2 – 6x + 9y – 5 = 0 represents a pair of parallel straight lines and find the distance between them.
Solution:
S = 8x2 – 24xy + 18y2 – 6x + 9y – 5
= 2(2x – 3y)2 – 3(2x – 3y) – 5
= [2(2x – 3y) – 5] [(2x – 3y) + 1]
= (4x – 6y – 5) (2x – 3y + 1) = 0
The lines are 4x – 6y – 5 = 0 and 2x – 3y + 1 = 0
\(\frac{a_{1}}{a_{2}}\) = \(\frac{4}{2}\), \(\frac{b_{1}}{b_{2}}\) = \(\frac{-6}{-3}\) = 2
\(\frac{a_{1}}{a_{2}}\) = \(\frac{b_{1}}{b_{2}}\)
∴ The given equation represents a pair of parallel lines.
Distance between the lines
= 2\(\sqrt{\frac{g^{2}-a c}{a(a+b)}}\) = 2\(\sqrt{\frac{9+40}{8(8+18)}}\) = \(\frac{2.7}{2 \sqrt{52}}\) = \(\frac{7}{\sqrt{52}}\)
![]()
Question 19.
If the pair of lines represented by ax2 + 2hxy + by2 = 0 and ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 form a rhombus, prove that (a – b) fg + h(f2 – g2) = 0.
Solution:
Combined equation of OA and OB is ax2 + 2hxy + by2 = 0
Combined equation of AC, BC is ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
Point of intersection is C(\(\frac{h f-b g}{a b-h^{2}}\), \(\frac{g h-a f}{a b-h^{2}}\))
Equation of the diagonal is y = \(\frac{g h-a f}{h f-b g}\) . x
y(hf – bg) = x(gh – af)
(gh – af) x – (hf- bg) y = 0
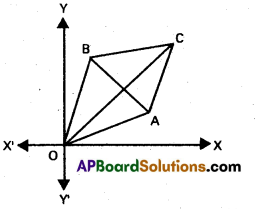
A and B are points on both this pair of lines.
Combined equation of AB is
2gx + 2fy + c = 0
OACB is a rhombus
OC and AB are perpendicular
2g(gh – af) – 2f(.hf – bg) = 0
hg2 – afg – hf2 + bfg = 0
(a – b) fg + h(f2 – g2) = 0
Question 20.
If two of the sides of a parallelogram are represented by ax2 + 2hxy + by2 = 0 and px + qy = 1 is one of its diagonals, prove that the other diagonal is y(bp – hq) = x(aq – hp).
Solution:
Let OACB be the parallelogram two of whose sides \(\overleftrightarrow{O A}\), \(\overleftrightarrow{O B}\) are represented by the equation H ≡ ax2 + 2hxy + by2 = 0. Since the other pair of sides \(\overleftrightarrow{A C}\) and \(\overleftrightarrow{B C}\) are respectively parallel to \(\overleftrightarrow{O B}\) and \(\overleftrightarrow{O A}\), their combined equation will be of the form S ≡ ax2 + 2hxy + by2 + 2gx + 2fy + c = 0. Then the equation of the diagonal \(\overleftrightarrow{A B}\) is 2gx + 2fy + c = 0. But this line is given to be px + qy = 1 (or) -pcx – qcy + c = 0 where c ≠ 0
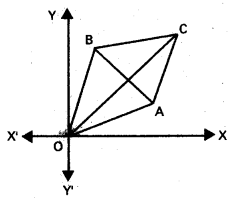
![]()
Therefore 2g = – pc, 2f = – qc …………….. (1)
The vertex C of the parallelogram = (\(\frac{h f-b g}{a b-h^{2}}\), \(\frac{g f-a f}{a b-h^{2}}\))
∴ Equation of the diagonal \(\overleftrightarrow{O C}\) is
(gh – af) x = (hf- bg)y
i.e., c(-ph + aq) x = c(-hq + bp)y (By 1)
(or) (aq – hp) x = (bp – hq) y (since c ≠ 0)
