Students get through Maths 1B Important Questions Inter 1st Year Maths 1B Limits and Continuity Important Questions which are most likely to be asked in the exam.
Intermediate 1st Year Maths 1B Limits and Continuity Important Questions
Question 1.
Evaluate ![]()
Solution:

Question 2.
Compute 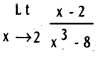
Solution:
Write f(x) = \(\frac{x-2}{x^{3}-8}\) x ≠ 2 so that
f(x) = \(\frac{x-2}{x^{3}-8}\) = \(\frac{1}{x^{2}+2 x+4}\)
Write h(x) = x2 + 2x + 4 so that
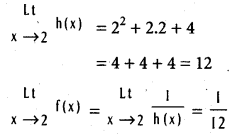
![]()
Question 3.
Find ![]()
Solution:
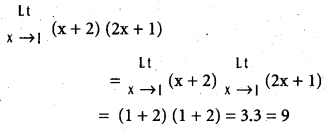
Question 4.
Compute 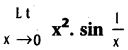 .
.
Solution:
For x ≠ 0, we know that -1 ≤ sin \(\frac{1}{x}\) ≤ 1
∴ -x2 ≤ x2 . sin \(\frac{1}{x}\) ≤ x2

Question 5.
Find 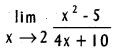 .
.
Solution:
We define f : R → R by f(x) = x2 – 5 and g : R → R by g(x) = 4x + 10.
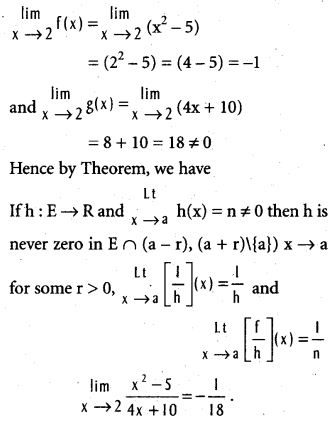
![]()
Question 6.
Find 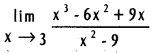 .
.
Solution:
Write F(x) = x3 – 6x2 + 9x
= x(x – 3)2 = (x – 3)
f(x) where f(x) = x(x – 3)
Write G(x) = x2 – 9 = (x – 3) (x + 3)
= (x – 3) g(x) where g(x) = x + 3
∴ \(\frac{F(x)}{G(x)}=\frac{(x-3) f(x)}{(x-3) g(x)}=\frac{f(x)}{g(x)}\)
and g(3) = 6 ≠ 0.
If F and G are polynomials such that f(x) = (x – a)k, G(x) = (x – a)k g(x) for some k ∈ N and for some polynomials f(x) and g(x) with
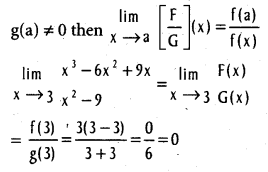
Question 7.
Find 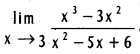 .
.
Solution:
We write F(x) = x3 – 3x2 = x2(x – 3) = (x – 3)
f(x) where f(x) = x2,
and G(x) = x2 – 5x + 6 = (x – 3)(x – 2)
= (x – 3) g(x) where g(x) = x – 2,
with g(3) = 3 – 2 = 1 ≠ 0.
∴ by applying Theorem g(a) ≠ 0
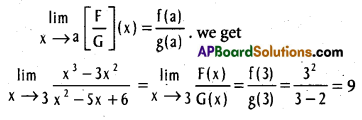
Question 8.
Show that 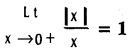 and
and 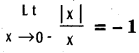 (x ≠ 0).
(x ≠ 0).
Solution:
![]()
Question 9.
Let f : R → R be defined by
f(x) = \(\begin{cases}2 x-1 & \text { if } x<3 \\ 5 & \text { if } x \geq 3\end{cases}\) show that  .
.
Solution:

Question 10.
Show that  .
.
Solution:
Observe that \(\sqrt{x^{2}-4}\) is not defined over (-2, 2)
Question 11.
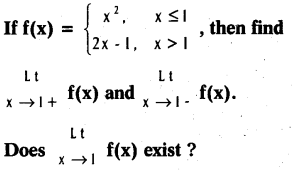
Solution:
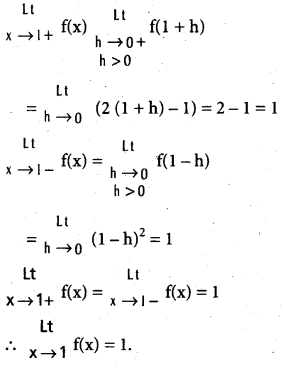
![]()
Question 12.
Show that 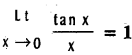 .
.
Solution:
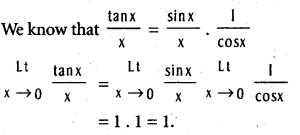
Question 13.
Find 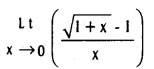
Solution:
For 0 < |x| < 1, we have
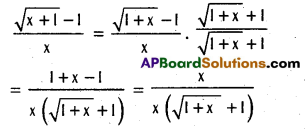
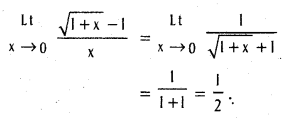
Question 14.
Compute 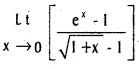
Solution:
For 0 < |x| < 1 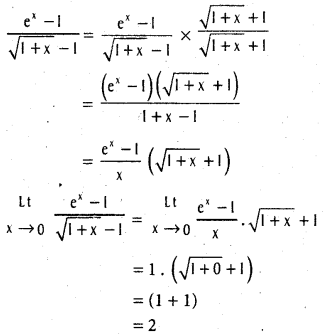
![]()
Question 15.
Show that 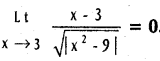
Solution:
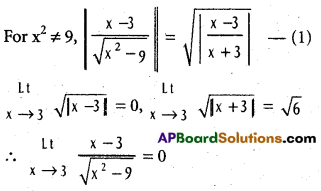
Question 16.
Compute [Mar 13] 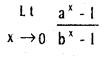 (a > 0, b > 0, b ≠ 1).
(a > 0, b > 0, b ≠ 1).
Solution:
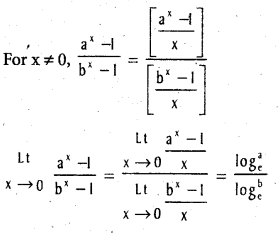
Question 17.
Compute 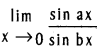 , b ≠ 0, a ≠ b.
, b ≠ 0, a ≠ b.
Solution:
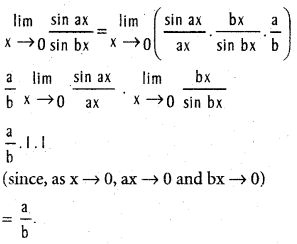
Question 18.
Compute 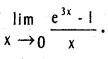
Solution:
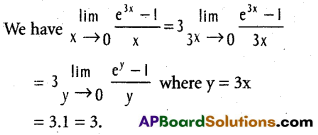
Question 19.
Compute 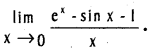
Solution:
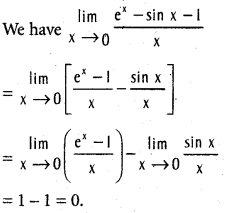
Question 20.
Evaluate 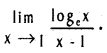
Solution:
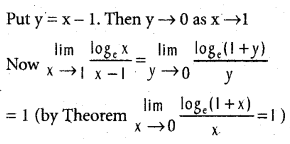
![]()
Question 21.
Show that 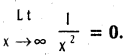
Solution:
Given ε > 0, choose ∞ = \(\frac{1}{\sqrt{\varepsilon}}\) > 0
x > ∞ ⇒ x > \(\frac{1}{\sqrt{\varepsilon}}\) ⇒ x2 > \(\frac{1}{\varepsilon}\) ⇒ \(\frac{1}{x^{2}}\) < ε
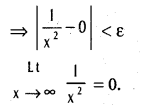
Question 22.
Show that ![]()
Solution:
Given k > 0, let ∞ = log k.
x > ∞ ⇒ ex ⇒ e∞ = k
![]()
Question 23.
Compute 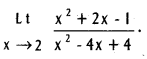
Solution:

Question 24.
Evaluate 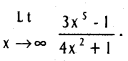 .
.
Solution:
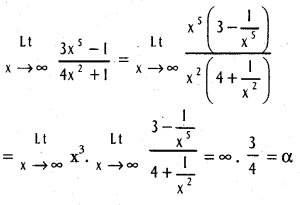
![]()
Question 25.
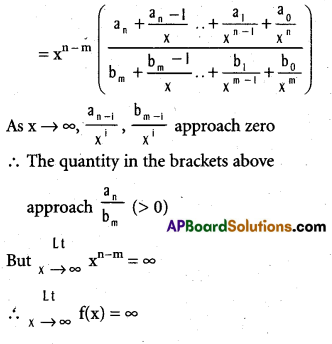
If f(x) \(\frac{a_{n} x^{n}+\ldots+a_{1} x+a_{0}}{b_{m} x^{m}+\ldots+b_{1} x+b_{0}}\) when an > 0, bm > 0, then show that 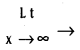 f(x) = ∞ if n > m.
f(x) = ∞ if n > m.
Solution:
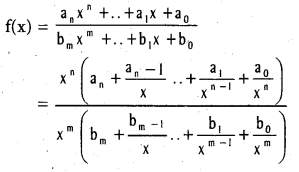
Question 26.
Compute 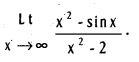
Solution:
-1 ≤ sinx ≤ 1 ⇒ -1 ≤ -sinx ≤ 1
x2 – 1 ≤ x2 – sinx ≤ x2 + 1
Since x → ∞, suppose that the x2 – 2 > 0
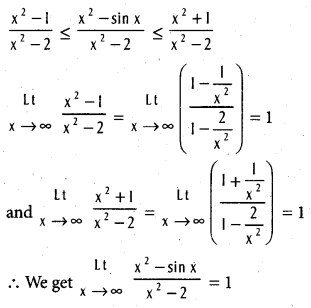
Question 27.
Show that f(x) = [x] (x ∈ R is continuous at only those real numbers that are not integers.
Solution:
Case i) : If a ∈ z, f(a) = (a) = a
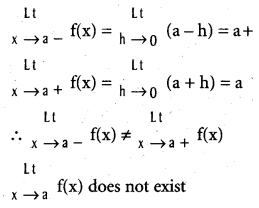
∴ f is not continuous at x = a ∈ z.
![]()
Case ii) : If a ∉ z, then ∃ n ∈ z such that n < a < n + 1 then f(a) = (a) = n.
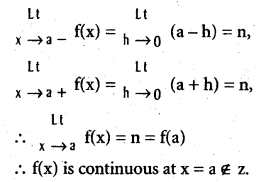
Question 28.
If f : R → R is such that f(x + y) = f(x) + f(y) for all x, y ∈ R then f is continuous on R if it is continuous at a single point in R.
Solution:
Let f be continuous at x0 ∈ R

∴ f is continuous at x.
Since x ∈ R is arbitrary, f is continuous on R.
Question 29.
Check the continuity of the function f given below at 1 and 2.
f(x) = \(\left\{\begin{array}{cl}
x+1 & \text { if } x \leq 1 \\
2 x & \text { if } 1<x<2 \\
1+x^{2} & \text { if } x \geq 2
\end{array}\right.\)
Solution:
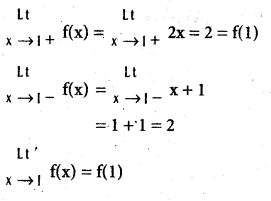
∴ f is continuous at x = 1
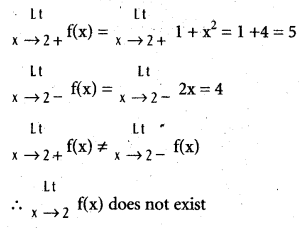
f is not continuous at x = 2.
Question 30.
Show that the function f defined on R by f(x) = Cos x2, x ∈ R is continuous function.
Solution:
We define h : R → R by h(x) = x2 and
g : R → R by g(x) = cosx.
Now, for x ∈ R
have (goh)(x) = g(h(x)) = g(x2)
= cos x2 = f(x)
Since g and h continuous on their respective domains, by Theorem
Let A, B, ⊆ R.
Let f : A → R be continuous on A and let
g : B → R be continuous on B.
If f(A) ⊆ B then the composite function
gof : A → R is continous on A.
It follows that a continuous function on R.
![]()
Question 31.
Show that the function f defined on R by f(x) = |1 + 2x + |x||, x ∈ R is a continuous function.
Solution:
We define g : R → R by
g(x) = 1 + 2x + |x|, x ∈ R,
and h : R → R by h(x) = |x|, x ∈ R. Then
(hog) (x) = h(g(x)) = h(1 + 2x + |x|)
= |1 + 2x + |x|| = f(x).
