Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Addition of Vectors Solutions Exercise 4(b) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1A Addition of Vectors Solutions Exercise 4(b)
I.
Question 1.
Find the vector equation of the line passing through the point \(2 \bar{i}+3 \bar{j}+\bar{k}\) and parallel to the vector \(4 \bar{i}-2 \bar{j}+3 \bar{k}\).
Solution:

Question 2.
OABC is a parallelogram. If \(\overline{O A}=\bar{a}\) and \(\overline{O C}=\bar{c}\), find the vector equation of the side BC.
Solution:
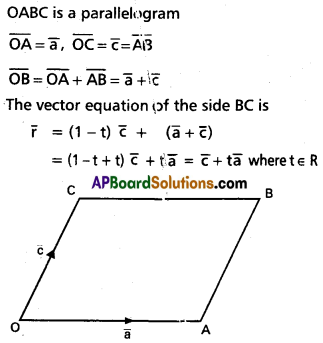
![]()
Question 3.
If \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) are the position vectors of the vertices A, B and C respectively of ∆ABC, theind the vector equation of the median through the vertex A.
Solution:

Question 4.
Find the vertor equation of the line joining the points \(2 \bar{i}+\bar{j}+3 \bar{k}\) and \(-4 \bar{i}+3 \bar{j}-\bar{k}\).
Solution:

Question 5.
Find the vector equation of the plane passing through the points \(\overline{\mathbf{i}}-2 \overline{\mathbf{j}}+5 \overline{\mathbf{k}},-5 \overline{\mathbf{j}}-\overline{\mathbf{k}} \text { and }-3 \overline{\mathbf{i}}+5 \overline{\mathbf{j}}\).
Solution:

![]()
Question 6.
Find the vector equation of the plane through the points (0, 0, 0), (0, 5, 0) and (2, 0, 1).
Solution:

II.
Question 1.
If \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) are noncoplanar find the point of intersection of the line passing through the points \(2 \bar{a}+3 \bar{b}-\bar{c}\), \(3 \bar{a}+4 \bar{b}-2 \bar{c}\) with the line joining the points \(\bar{a}-2 \bar{b}+3 \bar{c}, \bar{a}-6 \bar{b}+6 \bar{c}\).
Solution:

Question 2.
ABCD is a trapezium in which AB and CD are parallel. Prove by vector methods, that the mid points of the sides AB, CD and the intersection of the diagonals are collinear.
Solution:
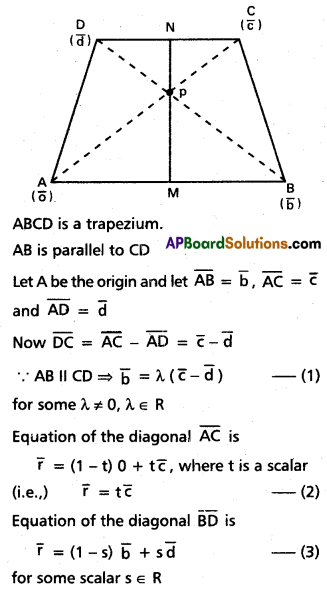



⇒ M, P, N are collinear
Hence the midpoints of parallel sides of a trapezium and the point of intersection of the diagonals are collinear.
![]()
Question 3.
In a quadrilateral ABCD, if the midpoints of one pair of opposite sides and the point of intersection of the diagonals are collinear, using vector methods, prove that the quadrilateral ABCD is a trapezium.
Solution:
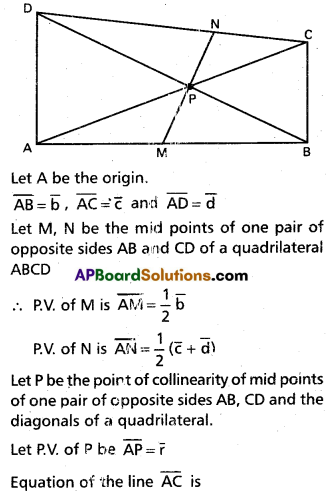

III.
Question 1.
Find the vector equation of the plane which passes through the points \(2 \bar{i}+4 \bar{j}+2 \bar{k}, 2 \bar{i}+3 \bar{j}+5 \bar{k}\) and parallel to the vector \(3 \overline{\mathbf{i}}-2 \overline{\mathbf{j}}+\overline{\mathbf{k}}\). Also find the point where this plane meets the line joining the points \(2 \overline{\mathbf{i}}+\overline{\mathbf{j}}+3 \overline{\mathbf{k}}\) and \(4 \bar{i}-2 \bar{j}+3 \bar{k}\).
Solution:



![]()
Question 2.
Find the vector equation of the plane passing through points \(4 \overline{\mathbf{i}}-3 \overline{\mathbf{j}}-\overline{\mathbf{k}}\), \(3 \overline{\mathbf{i}}+7 \overline{\mathbf{j}}-10 \overline{\mathbf{k}}\) and \(2 \bar{i}+5 \bar{j}-7 \bar{k}\), and show that the point \(\overline{\mathbf{i}}+2 \bar{j}-3 \overline{\mathbf{k}}\) lies in the plane.
Solution:


