AP SSC 10th Class Physics Solutions Chapter 6 Refraction of Light at Curved Surfaces

AP State Board Syllabus AP SSC 10th Class Physics Solutions Chapter 6 Refraction of Light at Curved Surfaces Textbook Questions and Answers.

AP State Syllabus SSC 10th Class Physics Solutions 6th Lesson Refraction of Light at Curved Surfaces

10th Class Physics 6th Lesson Refraction of Light at Curved Surfaces Textbook Questions and Answers

Review of Your Previous Knowledge

Question 1.
Have you ever touched a magnifying glass with your hand?
Answer:
Yes.

Question 2.
Have you touched the glass in the spectacles used for reading with your hand?
A. Yes.

Question 3.
Is it a plane or curved surface?
Answer:
Curved surface.

Question 4.
Is it thicker in the middle or at the edge?
Answeer:
Magnifying glass and some spectacle are thicker in middle whereas some spectacles are thicker at edge.

Improve Your Learning

Question 1.
A man wants to get a picture of a zebra. He photographed a white donkey after fitting a glass, with black stripes, on to the lens of his camera. What photo will he get? Explain. (AS1)
(OR)
A person wants to get a picture of zebra and he photographed a white donkey fitting a glass with black stripes. Does he get photo of zebra? Explain.
Answer:
The person was unable to gel the picture <>l zebra because only two rays are enough to form complete image after convergence. So he will get the image of white donkey but the intensity may be less.
(OR)
He will get a picture of while donkey because e\ery part of lens forms an image so if you cover lens with stripes still it forms a complete image. However, the intensity of the image will be reduced.

Question 2.
Two converging lenses are to be placed in the path of parallel rays so that the rays remain parallel after passing through both lenses. How should the lenses be arranged? Explain with a neat ray diagram. (AS1)
Answer:

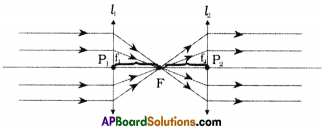
• Two lenses are placed in the path of parallel rays as shown in figure.
• The first lens is placed in the direction of parallel lines, which converges at focus.
• The second lens is arranged so that it is the focus of 2nd then emerging rays will be parallel.

Question 3.
The focal length of a converging lens is 20 cm. An object is 60 cm from the lens. Where will the image be formed and what kind of image is it? (AS1)
Answer:
f = 20 cm (by sign conversion f = + 20 cm)
u = 60 cm (by sign conversion u = – 60 cm)

Image will be formed at 30cm in between F₁, and 2F1. Image is real, inverted and diminished.

Question 4.
A double convex lens has two surfaces of equal radii ‘R’ and refractive index n = 1.5. Find the focal length ‘f’. (AS1)
(OR)
What is the focal length ‘f, when its double convex lens has two surfaces of equal radii ‘R’ and refractive index n = 1.5?
Answer:
R₁ = R₂ = R (suppose)
Focal length (f) = ?; Refractive index (n) = 1.5

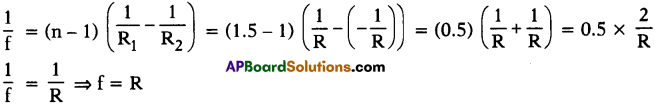
∴ Focal length of lens = Radius of curvature of surface.

Question 5.
Write the lens maker’s formula and explain the terms in it. (AS1)
(OR)
Ravi wants to make a lens. Which formula he has to follow ? Write the formula and explain the terms in it.
(OR)
Write lens formula.
Answer:
Lens maker’s formula:
\(\frac{1}{\mathrm{f}}=(\mathrm{n}-1)\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\)
n = Refractive index of the medium
R₁ = Radius of curvature of 1 st surface
R₂ = Radius of curvature of 2nd surface
f = Focal length

Question 6.
How do you verify experimentally that the focal length of a convex lens is increased when it is kept in water? (AS1)
(OR)
Write an activity to show that the focal length of a lens depends on its surrounding medium.
Answer:
Aim :
To prove focal length of convex lens is increased when it is kept in water.

Apparatus :
Convex lens, water, cylindrical vessel, circular lens holder, stone.

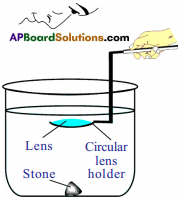
Procedure :

1. Take a cylindrical vessel like glass tumbler.
2. Its height must be greater than the focal length of lens, (the around four times focal length of lens).
3. Keep a black stone inside the vessel at its bottom.
4. Pour the water into the vessel such that the height of the water level from the top of the stone is greater than the focal length of lens.
5. Now dip the lens horizontally using a circular lens holder.
6. Set the distance between stone and lens that is equal to or less than focal length of lens.
7. Now see the stone through the lens.
8. We can see the image of the stone.
9. If we dip the lens to a certain height which is greater than the focal length of lens in air, still we can see the image.
10. This shows that the focal length of convex lens has increased in water.
11. Thus we conclude that the focal length of lens depends upon the surrounding medium.

Note : For convenience, use 5 or 10 cm focal length convex lens.

Question 7.
How do you find the focal length of a lens experimentally? (AS1)
Answer:

• Take the lens (Ex : Convex), which focused towards the distant object.
• A white coated screen (Ex : White paper) is placed on the other side of the lens.
• Adjust the screen till you get a clear image of the object.
• At this position measure the distance between the lens and screen which is equal to the focal length of the lens.

Question 8.
Harsha tells Siddhu that the double convex lens always behaves like a convergent lens. But Siddhu knows that Harsha’s assertion is wrong and corrected Harsha by asking some questions. What are the questions asked by Siddhu? (As2)
Answer:
The questions asked by Siddhu :

1. Is the object placed beyond 2f point?
2. Is the object located at 2f point?
3. Is the object located in between the 2f and the focal point?
4. Is the object located at the focal point?
5. Is the object located in front of the focal point?
6. Is the lens kept in a medium with refractive index less than lens or more than lens?

Question 9.
Assertion (A): A person standing on the land appears taller than his actual height to a fish inside a pond. (AS2)
Reason (R) : Light bends away from the normal as it enters air from water.
Which of the following is correct? Explain.
a) Both A and R are true and R is the correct explanation of A.
b) Both A and R are true and R is not the correct explanation of A.
c) A is true but R is false.
d) Both A and R are false.
e) A is false but R is true.
Answer:
Answer a is correct.
Explanation :
Because the light travelling from water to air it bends away from the normal so the fish observes the apparent image of the person, appears taller than his original.

Question 10.
A convex lens is made up of three different materials as shown in the figure Q-10. How many of images does it form? (AS2)

Answer:

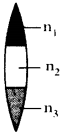
• A lens made of three different materials of refractive indices say n₁, n₂ and n₃.
• These three materials will have three different refractive indices. Thus for a given object it forms three images.

Question 11.
Can a virtual image be photographed by a camera? (AS2)
Answer:
Yes, we can.
Ex : – A plane mirror forms a virtual image, we can able to take photograph of that image in plane mirror.

Question 12.
You have a lens. Suggest an experiment to find out the focal length of the lens. (AS3)
(OR)
Through an experiment, find out the focal length of the lens.
Answer:
Aim :
To find focal length of given lens.

Apparatus :
Object (candle), convex lens, v – stand, screen.

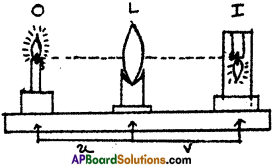
Procedure :

• Take a v-stand and place it on a long table at the middle.
  Place a convex lens on the v-stand. Imagine the principal axis of the lens.
• Light a candle and ask your friend to take the candle far away from the lens along the principal axis.
• Adjust a screen (a sheet of white paper placed perpendicular to the axis) which is on other side of the lens until you get an image on it.
• Measure the distance of the image from the v-stand of lens (image distance V) and also measure the distance between the candle and stand of lens (object distance ‘u’). Record the values in the table.

• Now place the candle at a distance of 60 cm from the lens, try to get an image of the candle flame on the other side on a screen. Adjust the screen till you get a clear image.
• Measure the image distance V and object distance ‘u’ and record the values in table.
• Repeat the experiment lor various object distances like 50 cm, 40 cm, 30 cm, etc. Measure the image distances in all cases and note them in table.
• Using the formula \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\), find f in all the cases. We will observe the value ‘f is equal in all cases. This value off is the focal length of the given lens.

Question 13.
Let us assume a system that consists of two lenses with focal length f₁, and f₂ respectively. How do you find the focal length of the system experimentally, when
i) two lenses are touching each other
ii) they are separated by a distance ‘d’ with common principal axis? (AS3)
Answer:
Experimental Proof:
i) Two lenses are touching each other :
Aim :
To find focal length of combination of two convex lenses, touching each other. Material required : Convex lenses – 2 (with known focal lengths say f, and f2); V-stands – 2, candle, screen scale.

Procedure:

• Place two V-stands with two convex lenses as they touch each other on a table.
• Place a candle (object) far away from the lenses.
• Adjust a screen, which is placed other side of the lenses until we get a clear image on it.
• At that position, measure the image distance (v) and object distance (u).
• Do this experiment for several object distances and record in the given table.

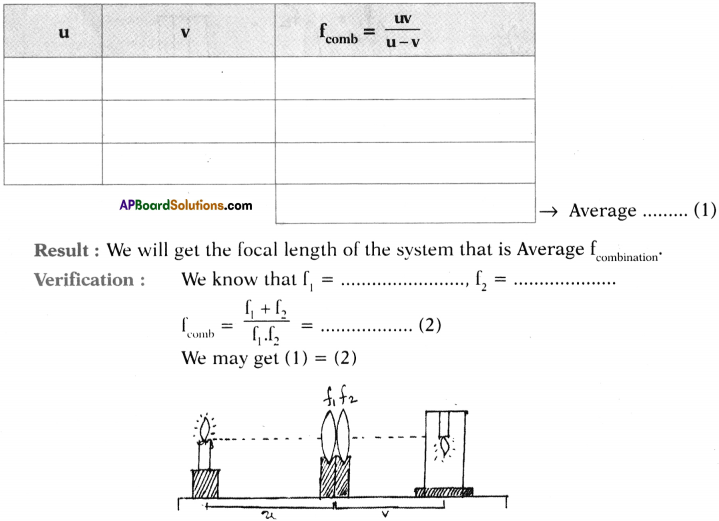
ii) They are separated by a distance of ‘d’ :
Procedure :

• Now place v-stands along with lenses with distance’d’.
• Do the same procedure again.
• Record the observations in the given table.
• Find the average of the ‘f’_comb.

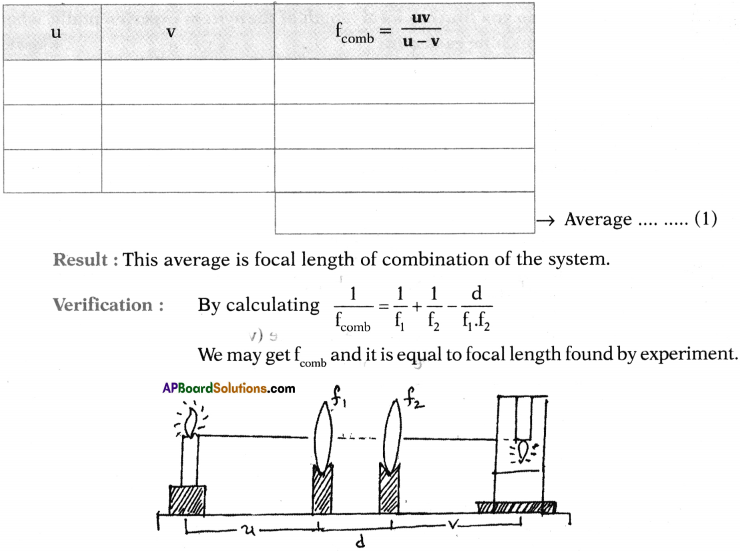
Question 14.
Collect the information about the lenses available in an optical shop. Find out how the focal length of a lens may be determined by the given power’ of the lens. (AS4)
Answer:
I had collected the information regarding different lenses available at optical shops.
The relationship between power and focal length is power (D) = \(\frac{1}{f}\). f is in meters.

Power of lens in diopters	Type of lens	Focal length
0.25	Convex	400 cm
0.5	Convex	200 cm
1	Convex	100 cm
-2	Concave	50 cm
– 1	Concave	– 100 cm
-0.5	Concave	– 200 cm
-0.25	Concave	– 400 cm

Question 15.
Collect the information about lenses used by Galileo in his telescope. (AS4)
(OR)
What lenses are used by Galileo in his telescope?
Answer:

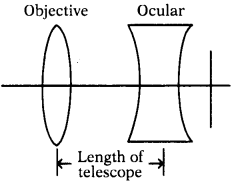
A Galilean telescope is defined as having one convex lens and one concave lens. The concave lens serves as the ocular lens or the eye piece, while the convex lens serves as the objective. The lens are situated on either side of a tube such that the focal point of the ocular lens is the same as the focal point for the objective lens.

Question 16.
Use the data obtained by activity – 2 in table-1 of this lesson and draw the graphs of u vs v and \(\frac{1}{u}\) vs \(\frac{1}{v}\) (AS5)
(OR)
By obtaining data from activity – 2 in table – 1 of this lesson, draw the graphs of u vs v and \(\frac{1}{u}\) vs \(\frac{1}{v}\)
Answer:
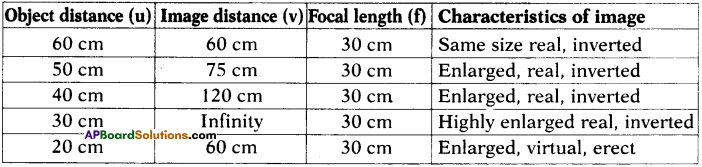
Graph of u – v using data obtained by activity – 2. Take lens with focal length 30 cm.

Object distance (u)	Image distance (v)	Focal length (f)
60 cm	60 cm	30 cm
50 cm	75 cm	30 cm
40 cm	120 cm	30 cm

The graph looks like this

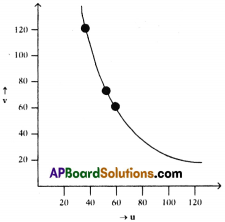
The shape of the graph is rectangular hyperbola.

Graph of \(\frac{1}{u}\) – \(\frac{1}{v}\)

For these values the graph is straight line which touches the axis as shown in figure.

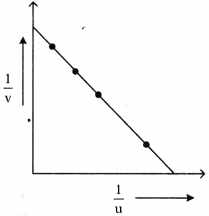
Question 17.
Figure shows ray AB that has passed through a divergent lens. Construct the path of the ray up to the lens if the F position of its foci is known. (AS5)

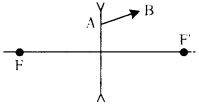
Answer:

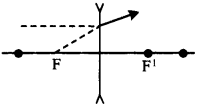
The path of the ray up to the lens if the position of foci is known for ray AB is diverging lens or concave lens path.

Question 18.
Figure shows a point light source and its image produced by a lens with an optical axis N₁, N₂. Find the position of the lens and its foci using a ray diagram. (AS5)

Answer:

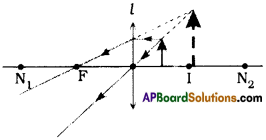
1. The object is in between focus and optic centre.
2. The image is virtual, erect and magnified. Nv
3. l is the lens, ‘O’ is the object and T is the image.

Question 19.
Find the focus by drawing a ray diagram using the position of source S and the image S’ given in the figure. (AS5)

Answer:

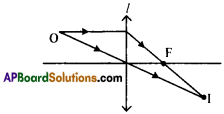
1.  Image is real.
2. l’ is lens, ‘O’ is object and T is image.
3.  Lens is convex.

(Or)

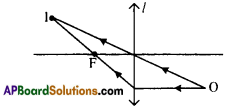
1. Image is real.
2. l’ is lens, ‘O’ is object and ‘I’ is image.
3. Lens is convex.

Question 20.
A parallel beam of rays is incident on a convergent lens with a focal length of 40 cm. Where should a divergent lens with a focal length of 15 cm be placed for the beam of rays to remain parallel after passing through the two lenses? Draw a ray diagram. (AS5)
Answer:

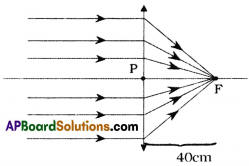
1. A parallel beam of rays when incident on a convergent lens, after refraction they meet at the focus of the lens.

2. A beam of rays which is incident on a divergent lens, after refraction, pass parallel to the principal axis. If we extend these incident rays, they seems to meet at focus of the lens.

3. Hence the divergent lens should be kept at 25 cm distance from convergent lens (40 – 15 = 25 cm) as shown in the figure.

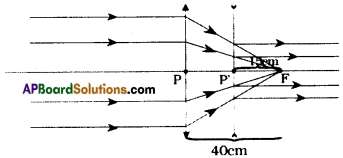
PF = 40 cm (Focal length of convergent lens)
P’F = 15 cm (Focal length of divergent lens)
PP’ = 40 – 15 = 25 cm (Position of divergent lens)

Question 21.
Draw ray diagrams for the following positions and explain the nature and position of image.
i) Object is placed at 2F₂
ii) Object is placed between F₂ and optic centre P. (AS5)
Answer:
i) Object is placed at 2F₂:

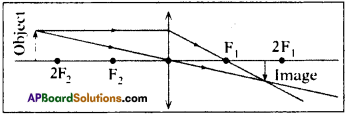
Nature : Real, inverted and diminished.
Position : Image is formed on the principal axis between the points F₁, and 2F₁.

ii) Object is placed between F₂ and optic centre P :

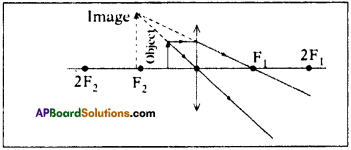
Nature : Virtual, erect and magnified.
Position : Same side of the lens where object is placed.

Question 22.
How do you appreciate the coincidence of the experimental facts with the results obtained by a ray diagram in terms of behaviour of images formed by lenses? (AS6)
Answer:

• Ray diagrams are very useful in optics.
• By the ray diagrams, we can easily find the values of image distance, object distance, focal length, radius of curvature, magnification, etc.
• These results are exactly equal to the result gotten by an experiment.
• For example : In the experiment, with a convex lens, we get clear image of an object, on a screen by adjusting the screen.

Then, we measure the image distane (v) practically. This takes more time and requires equipped lab also.

But, by simply draw a ray diagram on a paper, we can get exact image distance (v) very easily, without lab.

• So, ray diagrams are very useful in the construction of microscopes, telescopes, etc.
• Hence, one can trust and depend on the result of ray diagrams instead of several lab experiments.
• So, I appreciate the ray diagrams.

Question 23.
Find the refractive index of the glass which is a symmetrical convergent lens if its focal length is equal to the radius of curvature of its surface. (AS7)
Answer:
Given that lens is convergent symmetrical

Question 24.
Find the radii of curvature of a convexo – concave convergent lens made of glass with refractive index n = 1.5 having focal length of 24 cm. One of the radii of curvature is double the other. (AS7)
Answer:

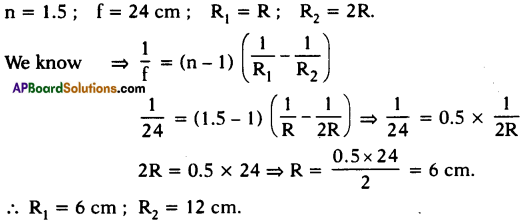
Question 25.
The distance between two point sources of light is 24 cm. Where should a convergent lens with a focal length of f = 9 cm be placed between them to obtain the images of both sources at the same point? (AS7)
Answer:
For Source S₁ :

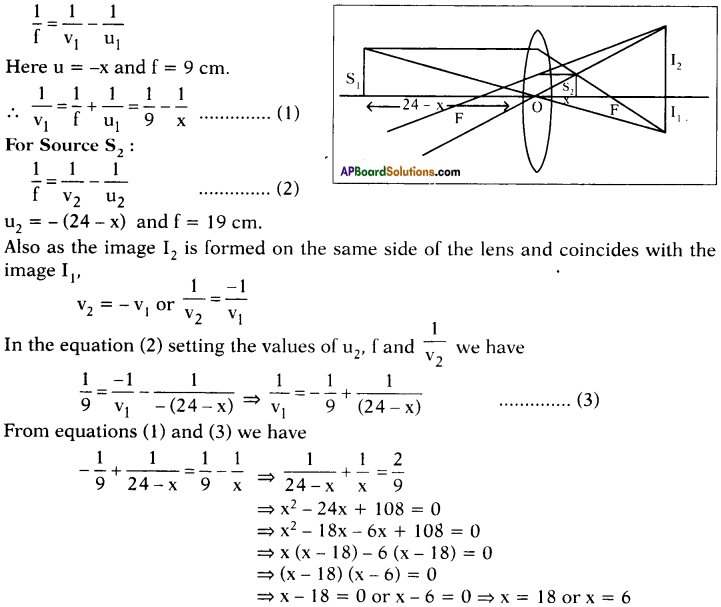
∴ The convex lens may be placed between the two sources, such that a distance of 18 cm from one source, and 6 cm from other source.

Question 26.
Suppose you are inside the water in a swimming pool near an edge. A friend is standing on the edge. Do you find your friend taller or shorter than his usual height? Why? (AS7)
(OR)
If your friend is standing near an edge of the swimming pool and you are in the water, do you find he is taller or shorter than his usual height?
Answer:

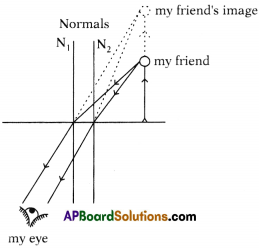
1. My friend appears to be taller because the light is travelling from rarer to denser.
2. The rays bend in such away that they seems to be coming from long distance.
3. So it is actually apparent image of my friend which appears to be taller due to refraction.

Fill in the Blanks

1. The rays from the distant object, falling on the convex lens pass through ……………….. .
2. The ray passing through the ……………….. of the lens is not deviated.
3. Lens formula is given by ……………….. .
4. The focal length of the plano-convex lens is 2R where R is the radius of curvature of the surface. Then the refractive index of the material of the lens is ……………….. .
5. The lens which can form real and virtual images is ……………….. .
Answer:

1. Tocus
2. optical centre
3. \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
4. 1.5
5. convex lens

Multiple Choice Questions

1. Which one of the following materials cannot be used to make a lens?
A) water
B) glass
C) plastic
D) clay
Answer:
D) clay

2. Which of the following is true?
A) The distance of virtual image is always greater than the object distance for convex lens.
B) The distance of virtual image is not greater than the object distance for convex lens.
C) Convex lens always forms a real image.
D) Convex lens always forms a virtual image.
Answer:
B) The distance of virtual image is not greater than the object distance for convex lens.

3. Focal length of the plano-convex lens is when its radius of curvature of the surface is R and n is the refractive index of the lens.

4. The value of the focal length of the lens is equal to the value of the image distance when the rays are
A) passing through the optic centre
B) parallel to the principal axis
C) passing through the focus
D) in all the cases
Answer:
D) in all the cases

5. Which of the following is the lens maker’s formula?

Answer:
C

10th Class Physics 6th Lesson Refraction of Light at Curved Surfaces Additional Questions and Answers

Question 1.
Derive a relation between refractive indices of two media (n₁, n₂), object distance (u), image distance (v) and radius of curvature (R) for a curved surface.
(OR)
Derive \(\frac{\mathbf{n}_{2}}{\mathbf{v}}-\frac{\mathbf{n}_{1}}{\mathbf{u}}=\frac{\mathbf{n}_{2}-\mathbf{n}_{1}}{\mathbf{R}}\)
(OR)
Derive curved surface formula.
Answer:

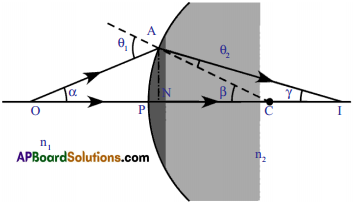
• Consider a curved surface separating two media of refractive indices n₁, and n₂.
• A point object is placed on the principal axis at point ‘O’.
• The ray which travels along the principal axis passes through the pole undeviated.
• The second ray, which forms an angle with a princi¬pal axis, meets the interface at A. The angle of incidence is Q₁. The ray bends and passes through the second medium along the line AI. The angle of refraction is Q₂.
• The two refracted rays meet at I and the image is formed there.
• 6) Let the angle made by the second refracted ray with principal axis be γ and the angle between the normal and principal axis be β.
• From figure,

PO = u (object distance), PI = v (Image distance),
PC = R (radius of curvature) and n₁, n₂ are refractive indices of the media.
From ∆ACO, θ₁ = α + β
∆ACI, β = θ₂ + γ
⇒ θ₂ = β – γ
According to Snell’s law, n₁sin θ₁ = n₂ sin θ₂.
∴ n₁ sin (α + β) = n₂ sin (β – γ) …………….. (1)
As per paraxial approximation,
sin (α + β) = α + β and sin (β – γ) = β – γ.
∴ (1) ⇒ n₁(α + β) = n₂ (β – γ)
⇒ n₁ α + n₁β = n₂ β – n₂ γ — (2)
Since all angles are small, we can write

∴ This is the required relation for curved surfaces.

Question 2.
Derive expression for lens maker’s formula.
(OR)
Prove \(\frac{1}{\mathbf{f}}=(\mathbf{n}-\mathbf{1})\left(\frac{1}{\mathbf{R}_{1}}-\frac{1}{\mathbf{R}_{2}}\right)\).
Answer:

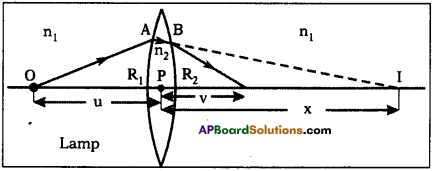
Procedure :

• Imagine a point object ‘O’ placed on the principal axis of the thin lens
• Let this lens be placed in a medium of refractive index n_a and let refractive index of lens be n_b.
• Consider a ray, from ‘O’ which is incident on the convex surface of the lens with radius of curvature R₁ at A.
• The incident ray refracts at A.
• It forms image at Q, if there were no concave surface.
• From figure Object distance PO = – u;

Image distance PQ = v = x
Radius of curvature R = R₁
n₁ = n_a and n₂ = n_b.

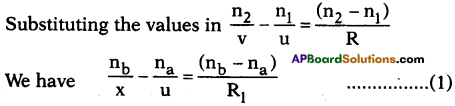
• But the ray that has refracted at A suffers another refraction at B on the concave surface with radius of curvature (R₂).
• At B the ray is refracted and reaches I.
• The image Q of the object due to the convex surface. So I is the image of Q for concave surface.
• Object distance u = PQ = + x
  Image distance PI = v
  Radius of curvature R = – R₂
• The refraction of the concave surface of lens is medium -1 and surrounding is medium – 2.
  ∴ n₁ = n_b and n₂ = n_a

Question 3.
Derive the lens formula.
Answer:
1. Consider an object 00′ placed on the principal axis in front of a convex lens as shown in the figure. Let II’ be the real image formed by the lens, i.e. the other side of it.

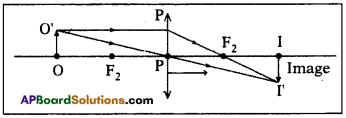
2. From the figure : PO, PI, PFt are the object distance, image distance and focal length respectively.

10th Class Physics 6th Lesson Refraction of Light at Curved Surfaces InText Questions and Answers

10th Class Physics Textbook Page No. 64

Question 1.
What happens to a ray that is incident on a curved interface separating the two media? Are the laws of refraction still valid?
Answer:
It undergoes deviation from its path. Yes, the laws of reflection are still valid.

Question 2.
How do rays betid when they are incident on a curved surface?
Answer:
A ray will bend towards the normal when it travels from rarer to denser medium and bends away from the normal when it travels from denser to a rarer medium.

10th Class Physics Textbook Page No. 65

Question 3.
What happens to ray that travels along the principal axis? Similarly, a ray that travels through the centre of curvature?

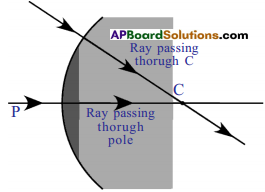
Answer:
According to Snell’s law the ray which travels along the normal drawn to the surface does not deviate from its path. Hence both rays in the given condition travel along normal, so they do not deviate.

Question 4.
What difference do you notice in the refracted rays in 4 (a) and 4 (b)? What could be the reason for that difference?

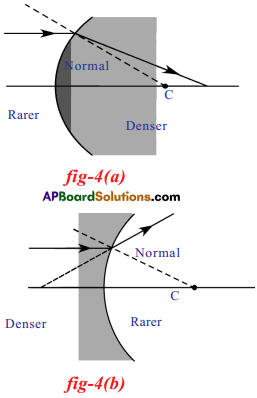
Answer:

• In figure 4 (a) ray travelling parallel to the principal axis strikes a convex surface and passes from a rarer medium to a denser medium.
• In figure 4 (b) a ray travelling parallel to the principal axis strikes a convex surface passes from a denser medium to a rarer medium.
• Figure 4 (a) : The refracted ray moves towards the normal.
• Figure 4 (b) : The refracted ray moves away from the normal.
  Reason : The main reason is that light passes through different media.

10th Class Physics Textbook Page No. 66

Question 5.
What difference do you notice in refracted rays in 4 (c) and 4 (d)? What could be the reasons for that difference?
(OR)
Draw the ray diagrams when the incident ray passes through the curved surfaces.
a) Rarer medium to denser medium.
b) Denser medium to rarer medium.

Answer:

• In figure 4 (c) a ray travelling parallel to the principal axis strikes a concave surface and passes from a denser medium to a rarer medium.
• In figure 4 (d) a ray travelling parallel to the principal axis strikes a concave surface and passes from a rarer medium to a denser medium.

Reasons :

• Figure 4 (c) :The refracted ray reaches a particular point on the principal axis.
• Figure 4 (d) : The refracted ray moves away from the principal axis.
• The main reason is that light passes through different media.

Question 6.
You might have observed that a lemon in the water of a glass tumbler appears bigger than its actual size, when viewed from the sides of tumbler.
1) How can you explain this (appeared) change in size of lemon?
Answer:
It can be explained by using refraction. When light travels from one medium to another medium it undergoes refraction.

2) Is the lemon that appears bigger in size an image of lemon or is it the real lemon?
Answer:
That is image of lemon.

3) Can you draw a ray diagram to explain this phenomenon?
Answer:

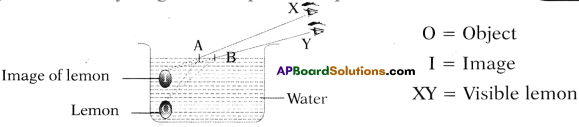
10th Class Physics Textbook Page No. 70

Question 7.
What happens to the light ray when a transparent material with two curved surfaces is placed in its path?
Answer:
The light ray undergoes refraction.

Question 8.
Have you heard about lenses?
Answer:
Yes, we have heard about lenses. A transparent material bounded by two spherical v surfaces is called lens.

Question 9.
How does a light ray behave when it is passed through a lens?
Answer:
A light ray will deviate from its path in some cases and does not deviate in some other cases.

10th Class Physics Textbook Page No. 72

Question 10.
How does the lens form an image?
Answer:
Lens forms an image through converging light rays or diverging light rays.

Question 11.
If we allow a light ray to pass through the focus, which path does it take?
Answer:
The ray passing through the focus takes a parallel path to principal axis after refraction.

10th Class Physics Textbook Page No. 73

Question 12.
What happens when parallel rays of light fall on a lens making some angle with the principal axis?
Answer:’
The rays converge at a point (or) appear to diverge from a point lying on the focal plane.

Question 13.
What do you mean by an object at infinity? What type of rays fall on the lens?
Answer:
The distance between the lens and the object is very much greater than when compared to object size is known as object at infinity. Parallel rays fall on the lens.
The object at infinity means distant object. The rays falling on the lens from an object at infinity are parallel to principal axis.

10th Class Physics Textbook Page No. 77

Question 14.
Could you get an image on the screen for every object distance with a convex lens?
Answer:
No, when the object is placed between pole and focus we will get virtual, erect and enlarged image on the other side of the- object.

Question 15.
Why don’t you get an image for certain object distances?
Answer:
Because at those distances the light rays diverge each other.

Question 16.
Can you find the minimum limiting object distance for obtaining a real image? What do you call this minimum limiting object distance?
Answer:
Yes, this minimum limiting object distance is called focal length.

Question 17.
When you do not get an image on the screen, try to see the image with your eye directly from the place of the screen. Could you see the image? What type of image do you see?
Answer:
Yes, we can see the image. This is a virtual image which we cannot capture on screen.

Question 18.
Can you find the image distance of a virtual image? How could you do it?
Answer:
We can find the image distance of virtual image by using lens formula \(\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{v}}-\frac{1}{\mathrm{u}}\) (if we know the focal length of lens and object distance.)

10th Class Physics 6th Lesson Refraction of Light at Curved Surfaces Activities

Activity – 1

Question 1.
Write an activity to observe the light refraction at curved surface.
Answer:
Procedure and observation :

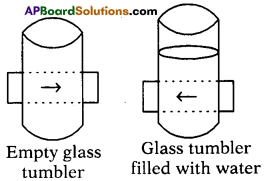
• Draw an arrow of length 4 cm usfng a black sketch pen on a thick sheet of paper.
• Take an empty cylindrical-shaped transparent vessel.
• Keep it on the table.
• Ask your friend to bring the sheet of paper on which arrow was drawn behind the vessel while you look at it from the other side.
• We will see a diminished image of the arrow.
• Ask your friend to fill vessel with water.
• Look at the arrow from the same position as before.
• We can observe an inverted image.

Explanation :

• In the first case, when the vessel is empty, light from the arrow refracts at the curved interface, moves through the glass, enters in to air then it again undergoes refraction on the opposite curved surface of vessel and comes out into the air.
• In this way light travels through two media, comes out of the vessel and forms a diminished image.
• In the second case, light enters the curved surface, moves through water, comes out of the glass and forms an inverted image.

Lab Activity

Question 2.
Write an activity to know the characteristics of image due to convex lens at various distances.
Answer:
Aim:
Determination of focal length of bi-convex lens using UV method.

Material Required :
V Stand, convex lens, light source, screen, meter scale. Take a V-stand and place it on a long (nearly 2m) table at the middle. Place a convex lens on the v-stand. Imagine the principal axis of the lens. Light a candle and ask your friend to take the candle far away from the lens along the principal axis. Adjust a screen (a sheet of white paper placed perpendicular to the axis) which is on other side of the lens until you get an image on it.

Procedure :

1. Take a V-stand and place a convex lens on this stand.
2. Imagine the principal axis of the lens.
3. Light a candle and ask your friend to take the candle far away from the lens along the principal axis.
4. We use a screen because it forms a real image generally which will form on a screen. Real images cannot be seen with an eye.
5. Adjust the screen, on other side of lens until clear image forms on it.
6. Measure the distance of the image from the stand and also measure the distance between the candle and stand of lens.
7. Now place the candle at a distance of 60 cm from the lens such as the flame of the candle lies on the principal axis of the lens.
8. Try to get an image of candle flame on the other side on a screen.
9. Adjust the screen till you get a clear image.
10. Measure the distance of image (v) from lens and record the value of’u’ and V in the table.
11. Repeat this for various distances of images; in all cases note them in the table.

Observation :

Conclusion : From this we conclude that a convex lens forms both real and virtual images when object is placed at various positions.