AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 9th Lesson Tangents and Secants to a Circle Exercise 9.3
10th Class Maths 9th Lesson Tangents and Secants to a Circle Ex 9.3 Textbook Questions and Answers
Question 1.
A chord of a circle of radius 10 cm. subtends a right angle at the centre. Find the area of the corresponding: (use π = 3.14)
i) Minor segment ii) Major segment
Answer:
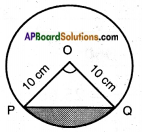
Angle subtended by the chord = 90° Radius of the circle = 10 cm
Area of the minor segment = Area of the sector POQ – Area of △POQ
Area of the sector = \(\frac{x}{360}\) × πr2
\(\frac{90}{360}\) × 3.14 × 10 × 10 = 78.5
Area of the triangle = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × 10 × 10 = 50
∴ Area of the minor segment = 78.5 – 50 = 28.5 cm2
Area of the major segment = Area of the circle – Area of the minor segment
= 3.14 × 10 × 10 – 28.5
= 314 – 28.5 cm2
= 285.5 cm2
![]()
Question 2.
A chord of a circle of radius 12 cm. subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle.
(use π = 3.14 and √3 = 1.732)
Answer:
Radius of the circle r = 12 cm.
Area of the sector = \(\frac{x}{360}\) × πr2
Here, x = 120°
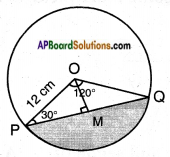
\(\frac{120}{360}\) × 3.14 × 12 × 12 = 150.72
Drop a perpendicular from ‘O’ to the chord PQ.
△OPM = △OQM [∵ OP = OQ ∠P = ∠Q; angles opp. to equal sides OP & OQ; ∠OMP = ∠OMQ by A.A.S]
∴ △OPQ = △OPM + △OQM = 2 . △OPM
Area of △OPM = \(\frac{1}{2}\) × PM × OM

= 18 × 1.732 = 31.176 cm
∴ △OPQ = 2 × 31.176 = 62.352 cm2
∴ Area of the minor segment
![]() = (Area of the sector) – (Area of the △OPQ)
= (Area of the sector) – (Area of the △OPQ)
= 150.72 – 62.352 = 88.368 cm2
Question 3.
A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm. sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades. (use π = \(\frac{22}{7}\))
Answer:
Angle made by the each blade = 115°
Total area swept by two blades
= Area of the sector with radius 25 cm and angle 115°+ 115° = 230°
= Area of the sector = \(\frac{x}{360}\) × πr2
= \(\frac{230}{360}\) × \(\frac{22}{7}\) × 25 × 25
= 1254.96
≃ 1255 cm2
![]()
Question 4.
Find the area of the shaded region in figure, where ABCD is a square of side 10 cm. and semicircles are drawn with each side of the square as diameter (use π = 3.14).
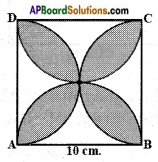
Answer:
Let us mark the four unshaded regions as I, II, III and IV.
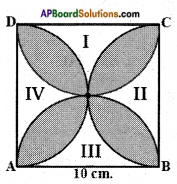
Area of I + Area of II
= Area of ABCD – Areas of two semicircles with radius 5 cm
= 10 × 10 – 2 × \(\frac{1}{2}\) × π × 52
= 100 – 3.14 × 25
= 100 – 78.5 = 21.5 cm2
Similarly, Area of II + Area of IV = 21.5 cm2
So, area of the shaded region = Area of ABCD – Area of unshaded region
= 100 – 2 × 21.5 = 100 – 43 = 57 cm2
Question 5.
Find the area of the shaded region in figure, if ABCD is a square of side 7 cm. and APD and BPC are semicircles. (use π = \(\frac{22}{7}\))
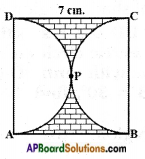
Answer:
Given,
ABCD is a square of side 7 cm.
Area of the shaded region = Area of ABCD – Area of two semicircles with radius \(\frac{7}{2}\) = 3.5 cm
APD and BPC are semicircles.
= 7 × 7 – 2 × \(\frac{1}{2}\) × \(\frac{22}{7}\) × 3.5 × 3.5
= 49 – 38.5
= 10.5 cm2
∴ Area of shaded region = 10.5 cm
![]()
Question 6.
In figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm., find the area of the shaded region, (use π = \(\frac{22}{7}\)).
Answer:
Given, OACB is a quadrant of a Circle.
Radius = 3.5 cm; OD = 2 cm.
Area of the shaded region = Area of the sector – Area of △BOD

= 9.625 – 3.5 = 6.125 cm2
∴ Area of shaded region = 6.125 cm2.
Question 7.
AB and CD are respectively arcs of two concentric circles of radii 21 cm. and 7 cm. with centre O (See figure). If ∠AOB = 30°, find the area of the shaded region. (use π = \(\frac{22}{7}\)).
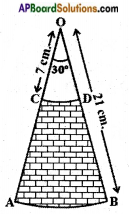
Answer:
Given, AB and CD are the arcs of two concentric circles.
Radii of circles = 21 cm and 7 cm and ∠AOB = 30°
We know that,
Area of the sector = \(\frac{x}{360}\) × πr2
Area of the shaded region = Area of the OAB – Area of OCD
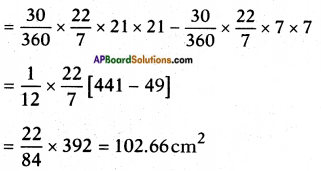
∴ Area of shaded region = 102.66 cm2
![]()
Question 8.
Calculate the area of the designed region in figure, common between the two quadrants of the circles of radius 10 cm each, {use π = 3.14)
Answer:
Mark two points P, Q on the either arcs.
Let BD be a diagonal of ABCD
Now the area of the segment

= 28.5 + 28.5 = 57 cm2
Side of the square = 10 cm
Area of the square = side × side
= 10 × 10 = 100 cm2
Area of two sectors with centres A and C and radius 10 cm.
= 2 × \(\frac{\pi r^{2}}{360}\) × x = 2 × \(\frac{x}{360}\) × \(\frac{22}{7}\) × 10 × 10
= \(\frac{1100}{7}\)
= 157.14 cm2
∴ Designed area is common to both the sectors,
∴ Area of design = Area of both sectors – Area of square
= 157 – 100 = 57 cm2
(or)
\(\frac{1100}{7}\) – 100 = \(\frac{1100-700}{7}\)
= \(\frac{400}{7}\)
= 57.1 cm2
