AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 6 Progressions Ex 6.5 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 6th Lesson Progressions Exercise 6.5
10th Class Maths 6th Lesson Progressions Ex 6.5 Textbook Questions and Answers
Question 1.
For each geometric progression find the common ratio ‘r’, and then find an.
i) 3, \(\frac{3}{2}\), \(\frac{3}{4}\), \(\frac{3}{8}\), …….
Answer:
Given G.P.: 3, \(\frac{3}{2}\), \(\frac{3}{4}\), \(\frac{3}{8}\), …….

ii) 2, -6, 18, -54, …….
Answer:
Given G.P. = 2, -6, 18, -54, …….
a = 2, r = \(\frac{a_{2}}{a_{1}}\) = \(\frac{-6}{2}\) = -3
an = a . rn-1 = 2 × (-3)n-1
∴ r = -3; an = 2(-3)n-1
![]()
iii) -1, -3, -9, -27, ……
Given G.P. = -1, -3, -9, -27, ……
a = -1, r = \(\frac{a_{2}}{a_{1}}\) = \(\frac{-3}{-1}\) = 3
an = a . rn-1 = (-1) × 3n-1
∴ r = 3; an = (-1) × 3n-1
iv) 5, 2, \(\frac{4}{5}\), \(\frac{8}{25}\), …….
Given G.P. = 5, 2, \(\frac{4}{5}\), \(\frac{8}{25}\), …….
a = 5, r = \(\frac{a_{2}}{a_{1}}\) = \(\frac{2}{5}\)
an = a . rn-1 = 5 × \(\left(\frac{2}{5}\right)^{n-1}\)
∴ r = \(\frac{2}{5}\); an = 5\(\left(\frac{2}{5}\right)^{n-1}\)
Question 2.
Find the 10th and nth term of G.P.: 5, 25, 125,…..
Answer:
Given G.P.: 5, 25, 125,…..
a = 5, r = \(\frac{a_{2}}{a_{1}}\) = \(\frac{25}{5}\) = 5
an = a . rn-1 = 5 × (5)n-1 = 51+n-1 = 5n
a10 = a . r9 = 5 × 59 = 510
∴ a10 = 510; an = 5n
Question 3.
Find the indicated term of each geometric progression.
i) a1 = 9; r = \(\frac{1}{3}\); find a7.
Answer:
an = a . rn-1

ii) a1 = -12; r = \(\frac{1}{3}\); find a6.
Answer:
an = a . rn-1
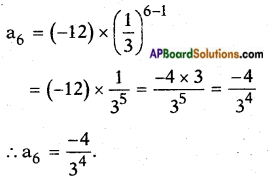
![]()
Question 4.
Which term of the G.P.
i) 2, 8, 32,….. is 512?
Answer:
Given G.P.: 2, 8, 32,….. is 512
a = 2, r = \(\frac{a_{2}}{a_{1}}\) = \(\frac{8}{2}\) = 4
Let the nth term of G.P. be 512

512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 29
∴ 2n – 1 = 9
[∵ bases are equal, exponents are also equal]
∴ 2n = 9 + 1 = 10
n = \(\frac{10}{2}\) = 5
∴ 512 is the 5th term of the given G.P.
ii) √3, 3, 3√3, …….. is 729?
Answer:
Given G.P.: √3, 3, 3√3, …….. is 729
a = √3, r = \(\frac{a_{2}}{a_{1}}\) = \(\frac{3}{\sqrt{3}}\) = √3
now an = a . rn-1 = 729
⇒ (√3)(√3)n-1 = 729
⇒ (√3)n = 36 = (√3)12
⇒ n = 12
So 12th term of GP √3, 3, 3√3, …….. is 729.
iii) \(\frac{1}{3}\), \(\frac{1}{9}\), \(\frac{1}{27}\), ……. is \(\frac{1}{2187}\)?
Answer:
Given G.P.: \(\frac{1}{3}\), \(\frac{1}{9}\), \(\frac{1}{27}\), ……. is \(\frac{1}{2187}\)
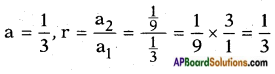
Let \(\frac{1}{2187}\) be the nth term of the G.P., then
an = a . rn-1 = \(\frac{1}{2187}\)
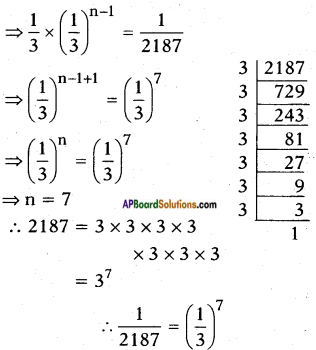
[∵ bases are equal, exponents are also equal]
7th term of G.P is \(\frac{1}{2187}\).
![]()
Question 5.
Find the 12th term of a G.P. whose 8 term is 192 and the common ratio is 2.
Answer:
Given a G.P. such that a8 = 192 and r = 2
an = a . rn-1
a8 = a . (2)8-1 = 192
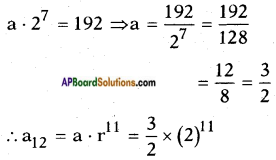
= 3 × 210 = 3 × 1024 = 3072.
Question 6.
The 4th term of a geometric progression is \(\frac{2}{3}\) and the seventh term is \(\frac{16}{81}\). Find the geometric series.
Answer:
Given: In a G.P.

Now substituting r = \(\frac{2}{3}\) in equation (1)
we get,

![]()
Question 7.
If the geometric progressions 162, 54, 18, ….. and \(\frac{2}{81}\), \(\frac{2}{27}\), \(\frac{2}{9}\),….. have their nth term equal, find the value of n.
Answer:
Given G.P.: 162, 54, 18, ….. and \(\frac{2}{81}\), \(\frac{2}{27}\), \(\frac{2}{9}\),……

Given that nth terms are equal
an = a . rn-1

⇒ 3n-1+n-1 = 81 × 81
⇒ 32n-2 = 34 × 34
⇒ 32n-2 = 38 [∵ am . an = am+n]
⇒ 2n – 2 = 8
[∵ bases are equal, exponents are also equal]
2n = 8 + 2
⇒ n = \(\frac{10}{2}\) = 5
The 5th terms of the two G.P.s are equal.
